Đề kiểm tra Hai đường thẳng song song (có lời giải) - Đề 1
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho hình chóp S.ABCD) có đáy ABCD là hình bình hành. Gọi \(I,J,E,F\) lần lượt là trung điểm SA,SB,SC,SD. Trong các đường thẳng sau, đường thẳng nào không song song với \[IJ?\]
\(AD\).
\(DC\).
\(EF\).
\(AB\).
Cho hình chóp tứ giác S.ABCD, gọi \(M\) và \(N\) lần lượt là trung điểm các cạnh \(SA\) và \(SC.\)Khi đó \(MN\) song song với đường thẳng
\(AC.\)
\(BC.\)
\(CD.\)
\(AD.\)
Cho hình chóp S.ABCD có ABCD là hình bình hành. Gọi \(I,J,E,F\) lần lượt là trung điểm SA,SB,SC,SD. Trong các đường thẳng sau, đường thẳng nào không song song với \[{\rm{IJ}}\]?
\(EF\).
\(DC\).
\(AD\).
\(AB\).
Cho tứ diện ABCD,\[G\]là trọng tâm tứ diện.Gọi\({G_1}\)là giao điểm của\[AG\]và mp\[\left( {BCD} \right)\],\({G_2}\)là giao điểm của\[BG\]và mp\[\left( {ACD} \right)\].Khẳng định nào sau đây là đúng?
\({G_1}{G_2}\,{\rm{//}}\,AB\).
\({G_1}{G_2}\,{\rm{//}}\,AC\).
\({G_1}{G_2}\,{\rm{//}}\,CD\).
\({G_1}{G_2}\,{\rm{//}}\,AD\).
Cho tứ diện ABCD.Gọi\(I\),\(J\)lần lượt là trọng tâm các tam giác ABC, ABD.Đường thẳng \(IJ\)song song với đường thẳng
\(AC\).
\(CD\).
\(CM\)với\(M\)là trung điểm cạnh\(BD\).
\(DB\).
Cho tứ diện ABCD. Gọi\(I\)và\(J\)lầnl ượt là trọng tâm\(\Delta ABC\)và\(\Delta ABD\). Chọn khẳng định đúng.
\(IJ\)song songvới\(CD\).
\(IJ\)song songvới\(AB\).
\(IJ\)chéo nhauvới\(CD\).
\(IJ\)cắt\(AB\).
Cho hình chóp S.ABC có \[E,{\rm{ }}F\]lần lượt là trung điểm cạnh \[AB,{\rm{ }}BC\]và điểm \[G\]thỏa mãn \[\overrightarrow {SG} = \frac{1}{2}\overrightarrow {SC} \]. Thiết diện của hình chóp \[S.ABC\]khi cắt bởi mặt phẳng \[\left( {EFG} \right)\]là hình nào dưới đây?
Tam giá.
Hình bình hành.
Hình thang chỉ có một cặp cạnh song song.
Hình thoi.
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm \(SA,{\rm{ }}SB\). \(P\) là một điểm trên cạnh \(BC\). Thiết diện tạo bởi mặt phẳng \(\left( {MNP} \right)\) với hình chóp có dạng là:
Hình chữ nhật.
Hình thang.
Hình tam giác.
Hình bình hành.
Cho t diện ABCD. Gọi \[N\] và \[P\] lần lượt là trung điểm của các cạnh \[BD\] và \[AD\]; \[M\] là điểm thuộc đoạn \[BC\] sao cho \[MC = 2MB\]. Kết luận nào sau đây đúng nhất về thiết diện của mặt phẳng \[\left( {MNP} \right)\] với hình chóp \[ABCD\]?
Thiết diện là ngũ giác.
Thiết diện là hình bình hành.
Thiết diện là hình thang.
Thiết diện là t giác.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm \(O\). Gọi \(I\) là điểm trên cạnh \(SO\). Mặt phẳng \(\left( {ICD} \right)\) cắt hình chóp theo thiết diện là hình gì?
Tam giác.
Hình thang.
Hình bình hành.
Hình chữ nhật.
Cho tứ diện ABCD. Gọi \(M\)và \(N\)lần lượt là trung điểm của \(AB\)và \(AC\). \(E\)là điển trên cạnh \(CD\)với \[ED = 3EC\]. Thiết diện tạo bởi mặt phẳng \(\left( {MNE} \right)\)và tứ diện \[ABCD\]là:
Tam giác \(MNE\).
Tứ giác \(MNEF\)với \(F\)là điểm bất kì trên cạnh \(BD\).
Hình bình hành \(MNEF\)với \(F\)là điểm bất kì trên cạnh \(BD\)mà \[EF\]song song với \(BC\)
Hình thang \(MNEF\)với \(F\)là điểm trên cạnh \(BD\)mà \[EF\]song song với \(BC\)
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành. Gọi \[I\] là trung điểm \[SA\]. Thiết diện của hình chóp c ắt bởi mặt phẳng \[\left( {IBC} \right)\] là
Tam giác \[IBC\].
Hình thang \[IBCJ\] (\[J\] là trung điểm \[SD\]).
Hình thang \[IGBC\] (\[G\] là trung điểm \[SB\]).
Tứ giác \[IBCD\].
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong các mệnh đề sau, mệnh đề nào đúng?
a) Hai đường thẳng không có điểm chung là hai đường thẳng song song hoặc chéo nhau.
b) Hai đường thẳng chéo nhau khi chúng không có điểm chung.
c) Hai đường thẳng song song khi chúng ở trên cùng một mặt phẳng.
d) Khi hai đường thẳng ở trên hai mặt phẳng thì hai đường thẳng đó chéo nhau.
Cho hình chóp S.ABCD có đáy là hình bình hành. Khi đó:
a) \(AB\) song song \(CD\)
b) \(SA\) cắt \(SC\);
c) \(SA\) song song \(BC\).
d) \(SC\) chéo nhau \(AB\).
Cho hình chóp S.ABCD có đáy là hình bình hành. Điểm \(M\) thuộc cạnh \(SA\), điểm \(E\) và \(F\) lần lượt là trung điểm của \(AB\) và \(BC\). Khi đó:
a) \(EF//AC\)
b) Giao tuyến của hai mặt phẳng \((SAB)\) và \((SCD)\) là đường thẳng qua \(S\) và song song với \(AC\).
c) Giao tuyến của hai mặt phẳng \((MBC)\) và \((SAD)\) đường thẳng qua \(M\) và song song với \(BC\).
d) Giao tuyến của hai mặt phẳng \((MEF)\) và \((SAC)\) là đường thẳng qua \(M\)và song song với \(AC\).
Cho tứ diện ABCD, gọi \(I\) và \(J\) lần lượt là trung điểm của \(AD\) và \(AC,G\) là trọng tâm của tam giác \(BCD\).
a) \(IJ//CD\)
b) Giao tuyến của hai mặt phẳng \((GIJ)\) và \((BCD)\) là đường thẳng qua \(G\) và song song với \(BC\)
c) Cho biết \(CD = 6\). Biết \((GIJ)\) cắt \(BC,BD\) lần lượt tại \(M\) và \(N\). Khi đó \(2IJ + 3MN = 17\).
d) Cho biết \(CD = 6\). Biết \((GIJ)\) cắt \(BC,BD\) lần lượt tại \(M\) và \(N\). Khi đó \(3IJ + 2MN = 18\).
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi \(G,H\) lần lượt là giao điểm của hai đường chéo của hai hình bình hành đó. Chứng minh rằng ba đường thẳng \(GH,CE,DF\) đôi một song song.
Cho tứ diện ABCD. Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AB,AD\) và \(P\) là một điểm nằm trên \(CD\). Đường thẳng \(BC\) cắt mặt phẳng \((MNP)\) tại \(Q\). Chứng minh rằng \(PQ//BD\)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi \(I,J\) lần lượt là trung điểm của các cạnh \(SA\) và \(SB\). Chứng minh rằng \(IJ//AB\), từ đó suy ra \(IJ//CD\).
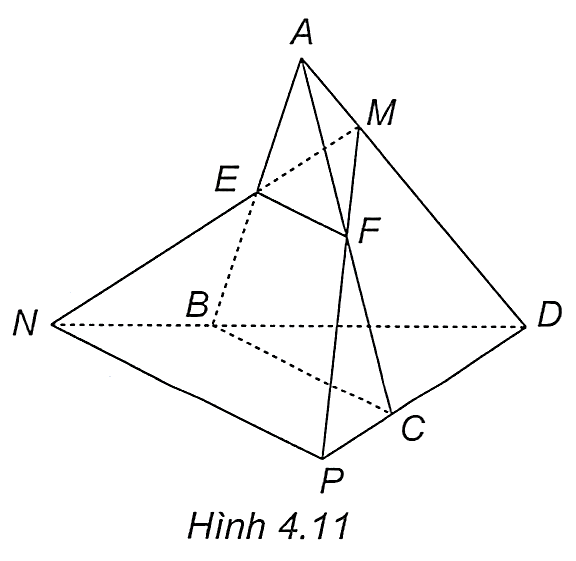
Cho tứ diện ABCD. Gọi \(E,F\) lần lượt là trung điểm của các cạnh \(AB,AC\) và \(M\) là một điểm bất kì thuộc cạnh \(AD\). Giả sử \(ME\) cắt \(BD\) tại \(N\) và \(MF\) cắt \(CD\) tại \(P(H.4.11)\). Chứng minh rằng \(NP//EF\).
Một chiếc gậy được đặt một đầu dựa vào tường và đầu kia trên mặt sàn (H.4.20).

Hỏi có thể đặt chiếc gậy đó song song với một trong các mép tường hay không?
Một bể kính chứa nước có đáy là hình chữ nhật được đặt nghiêng như Hình 4.26.
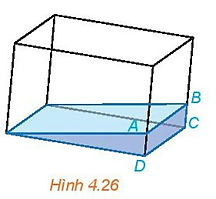
Giải thích tại sao đường mép nước \(AB\) song song với cạnh \(CD\) của bể nước.






