Đề kiểm tra Hai đường thẳng song song (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho tứ diện ABCD. Gọi \(I,J\) lần lượt là trọng tâm các tam giác ABC và ABD. Chọn khẳng định đúng trong các khẳng định sau.
\[{\rm{IJ}}\] song song với \(CD\).
\[{\rm{IJ}}\] song song với \(AB\).
\[{\rm{IJ}}\] chéo \(CD\).
\[{\rm{IJ}}\] cắt \(AB\).
Cho hình chóp S.ABCD. Gọi M,N,P,Q,R,T lần lượt là trung điểm AC,BD,BC,CD,SA,SD. Cặp đường thẳng nào sau đây song song với nhau?
\(MP\) và \(RT\).
\(MQ\) và \(RT\).
\(MN\) và \(RT\).
\(PQ\) và \(RT\).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và \[M\] là trung điểm cạnh \[SC\]. Khi đó thiết diện của hình chóp khi cắt bởi mặt phẳng \[\left( {MAB} \right)\] là
một tam giác.
một hình thang.
một hình bình hành.
một hình ngũ giác.
Cho tứ diện ABCD. \(M\) là một điểm bất kỳ nằm trên đoạn \(AC\) (khác \(A,C\)). Mặt phẳng \(\left( P \right)\) qua \(M\) và song song với các đường thẳng \(AB,CD\). Thiết diện của \(\left( P \right)\) với tứ diện đã cho là hình gì?
Hình chữ nhật.
Hình thang.
Hình vuông.
Hình bình hành.
Cho tứ diện ABCD. Gọi \[M\],\[N\] lần lượt là trung điểm của\[AB\] và\[AC\]. \[E\] là điểm trên cạnh \[CD\] và \[ED = 3EC\]. Thiết diện tạo bởi mặt phẳng \[\left( {MNE} \right)\] và tứ diện \[ABCD\] là
Tam giác \[MNE\].
Tứ giác \[MNEF\] với \[F\] là điểm bất kì trên cạnh \[BD\].
Hình bình hành \[MNEF\] với \[F\] là điểm trên cạnh \[BD\] mà \[EF\,{\rm{//}}\,BC\].
Hình thang \[MNEF\] với \[F\] là điểm trên cạnh \[BD\] mà \[EF\,{\rm{//}}\,BC\].
Cho tứ diện ABCD. Gọi \(I,J\)lần lượt là trọng tâm của tam giác ABC, ABD. Tìm khẳng định đúng trong các khẳng định sau đây.
Hai đường thẳng \[IJ\]và \(CD\)cắt nhau.
Hai đường thẳng \[IJ\]và \(CD\)chéo nhau.
Hai đường thẳng \[IJ\]và \(CD\)song song nhau và \[IJ = \frac{1}{3}CD\].
Hai đường thẳng \[IJ\]và \(CD\)song song nhau và \[IJ = \frac{2}{3}CD\].
Cho tứ diện ABCD, gọi các điểm \(M\), \(N\), \(P\), \(Q\) lần lượt là trung điểm các cạnh \(AB\), \(CD\), \(AC\) và \(BD\). Khi đó mệnh để nào sau đây đúng?
\(MN,PQ,BC\) đôi một song song.
\(MP\,{\rm{//}}\,BD\).
\(MN\,{\rm{//}}\,PQ\).
\(MP\,{\rm{//}}\,NQ\).
Cho hình chóp tứ giác S.ABCD. Gọi \({G_1},{G_2}\) lần lượt là trọng tâm các tam giác \(SAC\) và \(ACD.\) Khi đó \({G_1}{G_2}\) song song với đường thẳng
\(AC.\).
\(AD.\).
\(SD.\).
\(BC.\)
Cho tứ diện ABCD.Gọi\[G\]và\(E\)lần lượt là trọng tâm của tam giác\[ABD\]và\[ABC\].Mệnh đề nào dưới đây đúng
\(GE\)và\[CD\]chéo nhau.
\(GE{\rm{//}}CD\).
\[GE\]cắt\(AD\).
\(GE\)cắt\[CD\].
Cho tứ diện ABCD. Gọi \(M,N\) lần lượt là trung điểm của \(AB,AC\); \(E\) là điểm trên cạnh \(CD\) sao cho \(2EC = ED\). Khi đó, thiết diện tạo bởi \(\left( {MNE} \right)\) và tứ diện \(ABCD\) là hình gì?
Hình thang có đáy lớn là \(MN\).
Hình chữ nhật.
Hình bình hành.
Hình thang có đáy bé là \(MN\)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, \(I\) là trung điểm của \(SA\). Thiết diện của hình chóp \(S.ABCD\) cắt bởi mặt phẳng \(\left( {IBC} \right)\) là
\(\Delta IBC\).
Hình thang \[IJBC\] (\(J\) là trung điểm của \(SD\)).
Hình thang \[IGBC\](\(G\) là trung điểm của \(SB\)).
Tứ giác \(IBCD\).
Cho hình chóp S.ABCD có đáy ABCD là hình thang \[\left( {AD//BC} \right)\]. Gọi \[M,\,\,N,P\] lần lượt là trung điểm của \[SB\],\[CD\] và \[AC\]. Hãy cho biết thiết diện của hình chóp \[S.ABCD\]khi cắt bởi mặt phẳng \[\left( {MNP} \right)\] là hình gì?
Hình bình hành.
Hình thang.
Hình chữ nhật.
Hình tam giác.
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho mệnh đề nào sau đây đúng?
a) Nếu một mặt phẳng cắt một trong hai đường thẳng song song thì mặt phẳng đó sẽ cắt đường thẳng còn lại.
b) Hai mặt phẳng lần lượt đi qua hai đường thẳng song song thì cắt nhau theo một giao tuyến song song với một trong hai đường thẳng đó.
c) Nếu một đường thẳng cắt một trong hai đường thẳng song song thì đường thẳng đó sẽ cắt đường thẳng còn lại.
d) Hai mặt phẳng có một điểm chung thì cắt nhau theo một giao tuyến đi qua điểm chung đó.
Cho biết tính đúng sai của mỗi phát biểu sau (xét trong không gian):
a) Hai đường thẳng không có điểm chung thì chúng song song với nhau.
b) Hai đường thẳng không có điểm chung thì chúng chéo nhau.
c) Hai đường thẳng có điểm chung thì chúng cắt nhau.
d) Hai đường thẳng không thể cùng nằm trên một mặt phẳng thì chúng chéo nhau.
Cho tứ diện ABCD có \(I,J\) theo thứ tự là trung điểm của các cạnh \(BC\), \(BD\). Gọi \((P)\) là mặt phẳng qua \(I,J\) và cắt các cạnh \(AC,AD\) lần lượt tại hai điểm \(M,N\). Khi đó:
a) \(IJ = \frac{1}{2}CD\)
b) \(MN\) cắt \(DC\)
c) \(IJNM\) là một hình thang.
d) Để \(IJNM\) là hình bình hành thì \(M\) là trung điểm của đoạn \(AC\).
Cho hình chóp S.ABCD có đáy là hình bình hành, \(AC\) và \(BD\) cắt nhau tại \(O\). Gọi \(I\) là trung điểm \(SO\). Mặt phẳng \((ICD)\) cắt \(SA,SB\) lần lượt tại \(M,N\). Khi đó:
a) Điểm \(M\) là giao điểm của đường thẳng \(SA\) với mặt phẳng \((ICD)\)
b) Ta có \(SN = \frac{2}{3}SB\)
c) Cho \(AB = a\) thì \(MN = \frac{a}{2}\)
d) Trong mặt phẳng \((CDMN)\), gọi \(K\) là giao điểm của \(CN\) và \(DM\). Khi đó \(SK\) và \(BC\) chéo nhau
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho hình chóp tứ giác S.ABCD. Gọi \(G,K\) lần lượt là trọng tâm của các tam giác \(SAB\) và \(SAD;M,N\) lần lượt là trung điểm của \(BC\) và \(CD\). Chứng minh rằng \(GK//MN\).
Một chiếc thang được đặt sao cho hai đầu của chân thang dựa vào tường, hai đầu còn lại nằm trên sàn nhà \((H \cdot 4 \cdot 12)\).
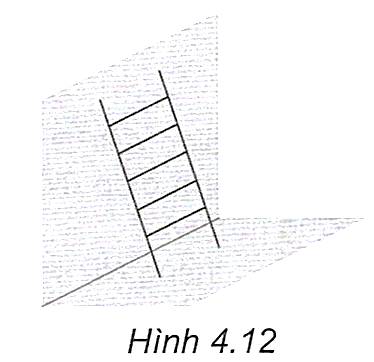
Biết rằng chiếc thang có dạng hình chữ nhật, hãy giải thích vì sao hai đầu của chân thang nằm trên sàn nhà lại cách đều đường chân tường.
Bạn Hà lấy một tờ giáy hình chữ nhật và gấp tờ giấy sao cho hai mép của tờ giấy song song với nhau \((H.4.13)\).

Hà thấy rằng dù gấp thế nào thì đường nếp gấp vẫn luôn song song với hai mép của tờ giấy. Hãy giải thích vì sao.
Cho hai hình bình hành \(ABCD\) và \(ABEF\) không cùng nằm trong một mặt phẳng (H.4.16).
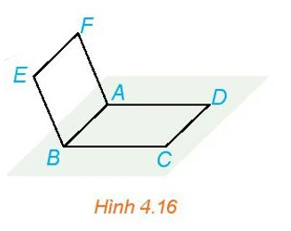
Chứng minh rằng bốn điểm \(C,D\),\(E,F\) đồng phẳng và tứ giác \(CDFE\) là hình bình hành.
Cho hình lập phương ABCD.A'B'C'D', \[AC \cap BD = O\].\[M\], \[N\] là trung điểm của \[A'B'\], \(BC\). Chứng minh \[MN{\rm{//}}A'O\].
Lăng trụ ABC.A'B'C'.\[M,P,Q\] là trung điểm \[A'B'\], \[B'C'\],\[AC\]. Chứng minh \[AM{\rm{//}}PQ\].






