Đề kiểm tra giữa học kì 2 Toán 10 Chân trời sáng tạo có đáp án - Đề 2
38 câu hỏi
Biểu thức nào dưới đây không phải là tam thức bậc hai?
f(x) = 2x2 + 5x – 3;
f(x) = x2 – 9;
f(x) = 32x2 + 3x + 4;
f(x) = x4 – 2x2 + 5.
Cho tam thức bậc hai f(x) = ax2 + bx + c, (a ≠ 0) và ∆ = b2 – 4ac. Mệnh đề nào sau đây đúng?
Nếu ∆ > 0 thì f(x) luôn cùng dấu với hệ số a, với mọi x ∈ ℝ;
Nếu ∆ < 0 thì f(x) luôn trái dấu với hệ số a, với mọi x ∈ ℝ;
Nếu ∆ = 0 thì f(x) luôn cùng dấu với hệ số a, với mọi x ∈ ℝ \ \(\left\{ { - \frac{b}{{2a}}} \right\}\);
Nếu ∆ < 0 thì f(x) luôn cùng dấu với hệ số b, với mọi x ∈ ℝ.
Tam thức bậc hai nào sau đây có biệt thức ∆ = 1 và có hai nghiệm là \({x_1} = \frac{3}{2}\) và \({x_2} = \frac{7}{4}\)?
8x2 – 26x + 21;
4x2 – 13x + \(\frac{{21}}{2}\);
4x2 + 4x – 15;
2x2 – 7x + 6.
Cho hàm số y = f(x) có đồ thị như hình dưới đây.
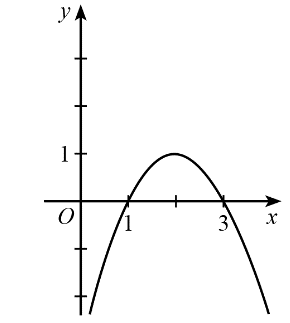
Trong các phát biểu sau, phát biểu nào sai?
f(x) < 0 khi và chỉ khi x ∈ (1; 3);
f(x) ≤ 0 khi và chỉ khi x ∈ (– ∞; 1] ∪ [3; + ∞);
f(x) > 0 khi và chỉ khi x ∈ (1; 3);
f(x) ≥ 0 khi và chỉ khi x ∈ [1; 3].
Tam thức nào sau đây luôn dương với mọi giá trị của x?
x2 – 10x + 2;
x2 – 2x – 10;
x2 – 2x + 10;
– x2 + 2x + 10.
Bất phương trình nào dưới đây là bất phương trình bậc hai một ẩn?
3x2 – 5x + 5 > 3x2 + 4x;
(x2)2 + 2x – 7 ≤ 0;
x4 + 2x2 – 9 > 0;
x2 + 2x – 3 ≥ 2x2 + x.
x = 0 là một nghiệm của bất phương trình nào sau đây?
2x2 + 3x + 1 < 0;
x2 + x – 3 > 0;
x2 + 2x + 4 < 0;
x2 – 3x – 1 < 0.
Giá trị nào dưới đây không là một nghiệm của bất phương trình – 2x2 + x + 1 ≥ 0?
x = 0;
x = – 1;
x = 1;
x = – 2.
Gọi S là tập nghiệm của bất phương trình x2 – 8x + 7 ≥ 0. Trong các tập hợp sau, tập nào không là tập con của S?
(– ∞; 0];
[6; + ∞);
[8; + ∞];
(– ∞; – 1].
Giá trị của m để phương trình – x2 + 2(m – 1)x + m – 3 = 0 có hai nghiệm phân biệt là
(– 1 ; 2);
(– ∞; – 1) ∪ (2; + ∞);
[– 1; 2];
(– ∞; – 1] ∪ [2; + ∞).
Phương trình \[\sqrt { - {x^2} + 4x} = 2x - 2\] có số nghiệm là
0;
1;
2;
3.
Giá trị nào sau đây là một nghiệm của phương trình\(\sqrt {3{x^2} - 6x + 1} = \sqrt {{x^2} - 3} \)?
2;
4;
12;
20.
Cho phương trình \(\sqrt { - {x^2} + 4x - 3} = \sqrt {2m + 3x - {x^2}} \) (1). Để phương trình (1) có nghiệm thì m ∈ [a; b]. Giá trị a2 + b2 bằng
2;
4;
1;
3.
Trong mặt phẳng tọa độ Oxy, cho vectơ \(\overrightarrow a = - 2\overrightarrow i + 3\overrightarrow j \). Tọa độ của vectơ \(\overrightarrow a \) là
(– 2; – 3);
(2; – 3);
(– 2; 3);
(2; 3).
Trong mặt phẳng tọa độ Oxy, cho A(2; 7) và B(– 2; 8). Độ dài đoạn thẳng AB là
5;
\(\sqrt {37} \);
\(\sqrt {17} \);
25.
Cho hai vectơ \(\overrightarrow x = \left( {3;\, - 4} \right)\), \(\overrightarrow y = \left( { - 6;\,\,8} \right)\). Khẳng định nào sau đây là đúng?
Hai vectơ \(\overrightarrow x ,\,\,\overrightarrow y \) bằng nhau;
Hai vectơ \(\overrightarrow x ,\,\,\overrightarrow y \) cùng phương cùng hướng;
Hai vectơ \(\overrightarrow x ,\,\,\overrightarrow y \) cùng phương ngược hướng;
Hai vectơ \(\overrightarrow x ,\,\,\overrightarrow y \) đối nhau.
Trong mặt phẳng tọa độ Oxy, cho M(3; – 6) và N(5; 2). Tọa độ trung điểm I của MN là
(4; – 2);
(1; 4);
(2; – 8);
(2; – 2).
Trong mặt phẳng tọa độ Oxy, cho hai vectơ \(\overrightarrow a = \left( {4;\,\, - m} \right)\) và \(\overrightarrow b = \left( {2m + 6;\,\,1} \right)\). Tập giá trị của m để hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương là
{– 1; 1};
{– 1; 2};
{– 2; – 1};
{– 2; 1}.
Cho tam giác ABC có A(1; 2), B(– 1; 1), C(5; – 1). Tính \(\overrightarrow {AB} \cdot \overrightarrow {AC} \).
7;
– 5;
5;
– 7.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: – x + 2y + 7 = 0. Vectơ pháp tuyến của đường thẳng d là
\(\overrightarrow n = \left( {1;\,\, - 2} \right)\);
\(\overrightarrow n = \left( { - 1;\,\,2} \right)\);
\(\overrightarrow n = \left( {2;\,\, - 1} \right)\);
\(\overrightarrow n = \left( {2;\,\,1} \right)\).
Phương trình tham số của đường thẳng ∆ đi qua điểm A(– 4; 2) và nhận \(\overrightarrow u = \left( {2;\,\, - 5} \right)\) làm vectơ chỉ phương là
\(\left\{ \begin{array}{l}x = 2 - 4t\\y = - 5 + 2t\end{array} \right.\);
\(\left\{ \begin{array}{l}x = - 4 + 2t\\y = 2 - 5t\end{array} \right.\);
\(\left\{ \begin{array}{l}x = 2 - 2t\\y = - 5 + t\end{array} \right.\);
\(\left\{ \begin{array}{l}x = - 4 + 2t\\y = 2 + 5t\end{array} \right.\).
Phương trình tổng quát của đường thẳng d đi qua điểm A(1; – 3) và nhận \(\overrightarrow n = \left( { - 2;\,\,7} \right)\) làm vectơ pháp tuyến là
2x – 7y + 23 = 0;
– 2x + 7y – 23 = 0;
2x – 7y – 23 = 0;
– 2x – 7y + 23 = 0.
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(3; – 1) và B(– 6; 2). Phương trình nào sau đây không phải là phương trình tham số của đường thẳng AB?
\(\left\{ \begin{array}{l}x = 3 + 3t\\y = - 1 - t\end{array} \right.\);
\(\left\{ \begin{array}{l}x = 3 + 3t\\y = - 1 + t\end{array} \right.\);
\(\left\{ \begin{array}{l}x = - 3t\\y = t\end{array} \right.\);
\(\left\{ \begin{array}{l}x = - 6 - 3t\\y = 2 + t\end{array} \right.\).
Khoảng cách từ điểm M(5; – 1) đến đường thẳng d: 3x + 2y + 13 = 0 là
\(2\sqrt {13} \);
\(\frac{{28}}{{\sqrt {13} }}\);
26;
\(\frac{{\sqrt {13} }}{2}\).
Góc giữa hai đường thẳng a: 6x – 5y + 15 = 0 và b: \(\left\{ \begin{array}{l}x = 10 - 6t\\y = 1 + 5t\end{array} \right.\) bằng
30°;
90°;
60°;
45°.
Phương trình nào sau đây là phương trình đường tròn?
x2 + 2y2 – 4x – 8y + 1 = 0;
x2 + y2 – 4x + 6y – 12 = 0;
x2 + y2 – 2x – 8y + 20 = 0;
4x2 + y2 – 10x – 6y – 2 = 0.
Đường tròn (x + 3)2 + (y – 4)2 = 16 có tâm là
I(3; 4);
I(3; – 4);
I(– 3; 4);
I(– 3; – 4).
Phương trình nào sau đây là phương trình của đường tròn tâm I(1; 2), bán kính bằng 5?
x2 + y2 – 2x – 4y – 20 = 0;
x2 + y2 + 2x + 4 + 20 = 0;
x2 + y2 + 2x + 4y – 20 = 0;
x2 + y2 – 2x – 4y + 20 = 0.
Phương trình đường tròn đường kính AB với A(1; 3) và B(5; – 1) là
(x + 3)2 + (y – 1)2 = 8;
(x + 3)2 + (y + 1)2 = 8;
(x – 3)2 + (y + 1)2 = 8;
(x – 3)2 + (y – 1)2 = 8.
Trong mặt phẳng tọa độ, cho đường tròn (C): x2 + y2 – 2x – 4y – 4 = 0 và điểm A(1; 5). Tiếp tuyến của đường tròn (C) tại điểm A có phương trình là
y – 5 = 0;
y + 5 = 0;
x + y – 5 = 0;
x – y – 5 = 0.
Trong mặt phẳng tọa độ Oxy, elip nào dưới đây có phương trình chính tắc dạng
\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\,\,\,\left( {a > b > 0} \right)\)?
A. 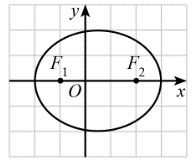 ;
;
B. 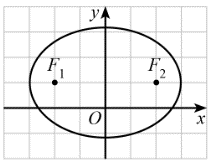 ;
;
C. 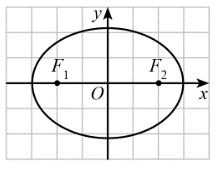 ;
;
D. 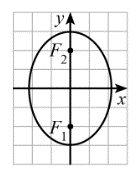 .
.
Trong mặt phẳng tọa độ Oxy, phương trình nào dưới đây là phương trình chính tắc của một hypebol?
\({x^2} - \frac{{{y^2}}}{2} = 1\);
\({x^2} + \frac{{{y^2}}}{3} = 1\);
\(\frac{{{x^2}}}{{{3^2}}} + \frac{{{y^2}}}{3} = - 1\);
\({x^2} - \frac{{{y^2}}}{5} = - 1\).
Trong mặt phẳng tọa độ Oxy, phương trình nào sau đây là phương trình chính tắc của parabol ?
y2 = 4x;
y2 = – 2x;
x2 = – 4y;
x2 = 2y.
Trong mặt phẳng tọa độ Oxy, cho elip (E): 16x2 + 25y2 = 400. Khẳng định nào sai trong các khẳng định sai?
(E) có trục nhỏ bằng 8;
(E) có tiêu cự bằng 3;
(E) có trục lớn bằng 10;
(E) có các tiêu điểm F1(– 3; 0) và F2(3; 0).
Đường hypebol \(\frac{{{x^2}}}{5} - \frac{{{y^2}}}{4} = 1\) có tiêu cự bằng
1;
2;
3;
6.
Viết phương trình tổng quát của đường thẳng
a) đi qua M(– 1; – 4) và song song với đường thẳng 3x + 5y – 2 = 0;
b) đi qua N(1; 1) và vuông góc với đường thẳng 2x + 3y + 7 = 0.
Hình dưới đây mô tả mặt cắt ngang của một chiếc đèn có dạng parabol trong mặt phẳng tọa độ Oxy (x và y tính bằng xen-ti-mét). Hình parabol có chiều rộng giữa hai mép vành là AB = 40 cm và chiều sâu h = 30 cm (h bằng khoảng cách từ O đến AB). Bóng đèn nằm ở tiêu điểm S. Viết phương trình chính tắc của parabol đó.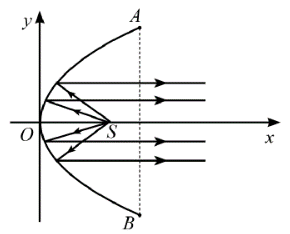
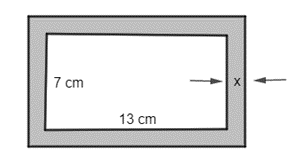
Hà dự định làm một khung ảnh hình chữ nhật sao cho phần trong của khung là hình chữ nhật có kích thước 7 cm × 13 cm, độ rộng viền xung quanh là x cm (như hình vẽ). Diện tích của viền khung ảnh không vượt quá 44 cm2. Hỏi độ rộng viền khung ảnh lớn nhất là bao nhiêu xen-ti-mét?