Bộ 5 đề thi giữa kì 2 Toán 10 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Đề 3
21 câu hỏi
Cho \(f\left( x \right) = a{x^2} + bx + c,\left( {a \ne 0} \right)\) có \(\Delta = {b^2} - 4ac < 0\). Khẳng định nào sau đây là đúng?
\(f\left( x \right)\) không đổi dấu trên \(\mathbb{R}\).
\(f\left( x \right) > 0,\forall x \in \mathbb{R}\).
Tồn tại \(x\) để \(f\left( x \right) = 0\).
\(f\left( x \right) < 0,\forall x \in \mathbb{R}\).
Cho các bất phương trình \(4{x^2} - 3x + 9 < 0;{x^2} - 5x < 0;4x - 3 > 0;4{x^2} + 1 > {x^3}\). Số lượng bất phương trình bậc hai một ẩn là:
\(3\).
\(2\).
\(1\).
\(4\).
Giá trị \(x = 2\) là nghiệm của phương trình nào sau đây?
\(x + 2 = \sqrt {x - 1} \).
\(x - 1 = \sqrt {x - 3} \).
\(x + 2 = 2\sqrt {3x - 2} \).
\(\sqrt {{x^2} - x - 4} = \sqrt {x - 4} \).
Trong mặt phẳng tọa độ \(Oxy\), tìm tọa tọa độ của \(\overrightarrow i \).
\(\overrightarrow i = \left( {0;1} \right)\).
\(\overrightarrow i = \left( { - 1;0} \right)\).
\(\overrightarrow i = \left( {0;0} \right)\).
\(\overrightarrow i = \left( {1;0} \right)\).
Cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 3 - 5t\\y = 1 + 4t\end{array} \right.\). Một vectơ chỉ phương của \(\Delta \) là:
\(\overrightarrow {{u_1}} = \left( {3;1} \right)\).
\(\overrightarrow {{u_2}} = \left( { - 5;4} \right)\).
\(\overrightarrow {{u_3}} = \left( {4;5} \right)\).
\(\overrightarrow {{u_4}} = \left( {1;3} \right)\).
Góc \(\varphi \) giữa hai đường thẳng \({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) và \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) được xác định theo công thức
\(\cos \varphi = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} + \sqrt {a_1^2 + b_1^2} }}\).
\(\cos \varphi = \sqrt {\frac{{{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}}}{{{a^2} + {b^2}}}} \).
\(\cos \varphi = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} \sqrt {a_2^2 + b_2^2} }}\).
\(\cos \varphi = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {a_1^2 + b_1^2} \sqrt {a_2^2 + b_2^2} }}\).
Đường tròn tâm \(I\left( {3; - 2} \right)\) và \(R = 5\) có phương trình là
\({\left( {x + 3} \right)^2} + {\left( {y - 2} \right)^2} = 5\).
\({\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} = 25\).
\({\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} = 5\).
\({\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} = 25\).
Cho elip \(\left( E \right)\) có phương trình chính tắc \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\). Tổng khoảng cách từ một điểm \(M\) bất kì trên \(\left( E \right)\) đến hai tiêu điểm là
\(6\).
\(4\).
\(3\).
\(9\).
Tập nghiệm của bất phương trình \( - {x^2} + 5x + 6 > 0\) là
\(\left( { - 1;6} \right)\).
\(\left\{ { - 1;6} \right\}\).
\(\left[ { - 1;6} \right]\).
\(\left( { - \infty ; - 1} \right) \cup \left( {6; + \infty } \right)\).
Tổng tất cả các nghiệm của phương trình \(\sqrt {{x^2} + 2x - 3} = \sqrt {15 - 5x} \) là
\(7\).
\( - 7\).
\(6\).
\(4\).
Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \[\Delta :\left\{ \begin{array}{l}x = 2 + 3t\\y = - 1 + t\end{array} \right.\left( {t \in \mathbb{R}} \right)\] và điểm \(M\left( { - 1;6} \right)\). Phương trình đường thẳng đi qua \(M\) và vuông góc với \(\Delta \) là:
\(x - 3y + 19 = 0\).
\(x + 3y - 17 = 0\).
\(3x - y + 9 = 0\).
\(3x + y - 3 = 0\).
Trong mặt phẳng \(Oxy\), đường tròn \(\left( C \right)\) đi qua hai điểm \(A\left( {5; - 1} \right),B\left( { - 3;7} \right)\). Đường tròn có đường kính \(AB\) có phương trình là
\({x^2} + {y^2} - 2x - 6y - 22 = 0\).
\({x^2} + {y^2} - 2x - 6y + 22 = 0\).
\({x^2} + {y^2} - 2x - y + 1 = 0\).
\({x^2} + {y^2} + 6x + 5y + 1 = 0\).
Cho tam thức bậc hai \(f\left( x \right) = - {x^2} + 11x - 24\).
a) Tam thức bậc hai đã cho có biệt thức \(\Delta = - 71\).
b) Tam thức bậc hai có hai nghiệm \(x = - 3\); \(x = - 8\).
c) \(f\left( x \right)\) nhận giá trị âm khi \(x \in \left( { - \infty ;3} \right) \cup \left( {8; + \infty } \right)\).
d) Có 6 giá trị nguyên của \(x\) để \(f\left( x \right)\) nhận giá trị không âm.
Trong mặt phẳng \(Oxy\), cho đường tròn \(\left( C \right)\) có phương trình \({x^2} + {y^2} - 6x + 2y + 6 = 0\) và hai điểm \(A\left( {1; - 1} \right),B\left( {1;3} \right)\).
a) Điểm \(A\) thuộc đường tròn.
b) Điểm \(B\) nằm trong đường tròn.
c) \(x = 1\) phương trình tiếp tuyến của \(\left( C \right)\) tại điểm \(A\).
d) Qua \(B\) kẻ được hai tiếp tuyến với \(\left( C \right)\) có phương trình lần lượt là \(x = 1\) và \(3x + 4y - 12 = 0\).
Bất phương trình \({x^2} - 8x + 16 \le 0\) có bao nhiêu nghiệm nguyên?
Trong mặt phẳng tọa độ \(Oxy\), cho parabol \(\left( P \right):{y^2} = 2px\left( {p > 0} \right)\). Biết khoảng cách từ tiêu điểm \(F\) đến đường thẳng \(\Delta :x + y - 12 = 0\) bằng \(2\sqrt 2 \). Tính tổng các giá trị của \(p\) thỏa mãn đề bài.
Một cửa hàng pháo hoa Bộ Quốc Phòng nhân dịp Tết Nguyên Đán đã đồng loạt giảm giá các sản phẩm pháo hoa. Trong đó có chương trình nếu mua một hộp pháo hoa thứ hai trở đi sẽ được giảm 10% so với giá ban đầu. Biết giá hộp đầu là 400000 đồng. Bác An có 5000000 đồng. Hỏi Bác An có thể mua tối đa bao nhiêu hộp pháo.
Trong mặt phẳng tọa độ \(\left( {Oxy} \right),\) cho điểm \(I\left( { - 2;\;1} \right)\) và đường thẳng \(\Delta :4x + 3y + 1 = 0.\) Tìm bán kính của đường tròn có tâm \(I\) và cắt đường thẳng \(\Delta \) tại hai điểm \(A,B\) sao cho tam giác \(IAB\) vuông (kết quả làm tròn đến hàng phần trăm).
Viết phương trình tham số của đường thẳng \(d\) đi qua \(A\left( {1;1} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {2;3} \right)\).
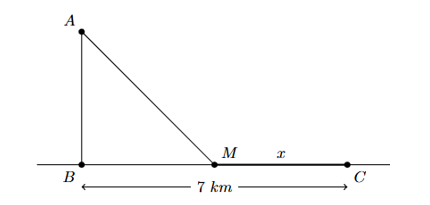
Người thứ nhất chèo thuyền với vận tốc 6 (km/h) vào bờ biển từ một ngọn hải đăng đặt tại vị trí \(A\) cách bờ biển một khoảng \(AB = 4\left( {{\rm{km}}} \right)\). Trên bờ biển, người thứ hai đi xe máy với vận tốc 10 (km/h) từ một nhà kho ở vị trí C cách \(B\) một khoảng \(BC = 7\)(km) (hình vẽ bên dưới). Xác định vị trí hai người gặp nhau ở vị trí \(M\) đến \(C\), biết hai người xuất phát cùng một lúc (kết quả làm tròn đến hàng phần chục).
Một elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > b > 0} \right)\) với bán trục lớn \(a\), bán tiêu cự \(c\) thì tỉ số \(e = \frac{c}{a}\) được gọi là tâm sai của elip. Quỹ đạo của trái đất quay quanh mặt trời là một elip \(\left( E \right)\), trong đó mặt trời là một trong các tiêu điểm. Biết khoảng cách nhỏ nhất và lớn nhất giữa mặt trời và trái đất lần lượt là 147 triệu km và 152 triệu km. Tìm tâm sai của elip \(\left( E \right)\).