Bộ 5 đề thi giữa kì 2 Toán 10 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Đề 4
21 câu hỏi
Cho tam thức bậc hai \(f\left( x \right) = - {x^2} + 6x - 5\) có bảng xét dấu như sau:

Mệnh đề nào sau đây đúng?
\(f\left( x \right) > 0,\forall x \in \left( { - \infty ;1} \right) \cup \left( {5; + \infty } \right)\).
\(f\left( x \right) < 0,\forall x \in \left( { - \infty ;1} \right) \cup \left( {5; + \infty } \right)\).
\(f\left( x \right) > 0,\forall x \in \mathbb{R}\).
\(f\left( x \right) < 0,\forall x \in \left( {1;5} \right)\).
Bất phương trình nào là bất phương trình bậc hai một ẩn?
\(2023x - 2022 < 0\).
\({x^2} - 2023x + 2022 \ge 0\).
\(\frac{{2023}}{{{x^2}}} + 2022x + 1 \ge 0\).
\({x^2} - \frac{{2023}}{x} + 2022 < 0\).
Kết quả nào dưới đây không phải là nghiệm của phương trình \(\sqrt {3{x^2} - 6x + 1} = \sqrt { - 2{x^2} - 9x + 1} \)?
\(x = 0\).
\(x = 0\)và \(x = - \frac{3}{5}\).
\(x = \frac{3}{5}\).
\(x = - \frac{3}{5}\)
Trong hệ tọa độ \(Oxy\), cho \(\overrightarrow u = \frac{1}{2}\overrightarrow i - 5\overrightarrow j \). Tọa độ vectơ \(\overrightarrow u \) là
\(\overrightarrow u = \left( {\frac{1}{2};5} \right)\).
\(\overrightarrow u = \left( {\frac{1}{2}; - 5} \right)\).
\(\overrightarrow u = \left( { - 1;10} \right)\).
\(\overrightarrow u = \left( {1; - 10} \right)\).
Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \(d:\left\{ \begin{array}{l}x = - 2t\\y = 4 + t\end{array} \right.\). Trong các vectơ sau, vectơ nào là vectơ pháp tuyến của \(d\)?
\(\overrightarrow {{n_1}} = \left( {1; - 2} \right)\).
\(\overrightarrow {{n_2}} = \left( { - 2;1} \right)\).
\(\overrightarrow {{n_3}} = \left( {3;6} \right)\).
\(\overrightarrow {{n_4}} = \left( {4;2} \right)\).
Đường thẳng nào sau đây song song với đường thẳng \(\Delta :2x + 3y - 1 = 0\)?
\(x - 2y + 5 = 0\).
\(2x + 3y + 1 = 0\).
\(2x - 3y + 3 = 0\).
\(4x - 6y - 2 = 0\).
Tìmtọa độ tâm \(I\) và bán kính \(R\) của đường tròn \(\left( C \right):{\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} = 8\).
\(I\left( { - 1;3} \right),R = 8\).
\(I\left( {1; - 3} \right),R = 8\).
\(I\left( { - 1;3} \right),R = 2\sqrt 2 \).
\(I\left( {1; - 3} \right),R = 2\sqrt 2 \).
Phương trình nào sau đây là phương trình chính tắc của đường hypebol?
\(\frac{{{x^2}}}{3} - \frac{{{y^2}}}{4} = 1\).
\(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{6} = 1\).
\(\frac{{{x^2}}}{{25}} - \frac{{{y^2}}}{{16}} = 0\).
\(\frac{{{y^2}}}{{16}} - \frac{{{x^2}}}{9} = 1\).
Cho đồ thị của hàm số bậc hai \(y = f\left( x \right)\) như hình vẽ
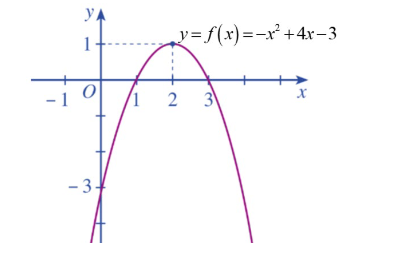
\(f\left( x \right) > 0 \Leftrightarrow x \in \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\).
\(f\left( x \right) > 0 \Leftrightarrow x \in \left[ {1;3} \right]\).
\(f\left( x \right) > 0 \Leftrightarrow x \in \left( {1;3} \right)\).
\(f\left( x \right) > 0 \Leftrightarrow x \in \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)\).
Số nghiệm nguyên dương của phương trình \(\sqrt {x - 1} = x - 3\) là
\(0\).
\(1\).
\(2\).
\(3\).
Tìm \(m\) để 2 đường thẳng \({\Delta _1}:2x - y + 1 = 0\) và \({\Delta _2}:4x - my + 7 = 0\) vuông góc với nhau?
\(m = 2\).
\(m = - 2\).
\(m = - 8\).
\(m = 8\).
Trong mặt phẳng \(Oxy\), đường tròn tâm \(I\left( { - 1;2} \right)\) và đi qua điểm \(M\left( {2;1} \right)\) có phương trình là:
\({x^2} + {y^2} + 2x - 4y - 5 = 0\).
\({x^2} + {y^2} + 2x - 4y - 3 = 0\).
\({x^2} + {y^2} - 2x - 4y - 5 = 0\).
\({x^2} + {y^2} + 2x + 4y - 5 = 0\)
Cho biểu thức \(f\left( x \right) = \left( {m - 2} \right){x^2} - 2\left( {m - 1} \right)x + 3\).
a) \(f\left( x \right)\) là tam thức bậc hai khi \(m \ne 2\).
b) Khi \(m = 3\) thì \(f\left( x \right) > 0\) với mọi \(x \in \mathbb{R}\).
c) \(f\left( x \right) < 0\) với mọi \(x \in \mathbb{R}\) khi và chỉ khi \(m < 2\) và \(\Delta < 0\).
d) Khi \(m = 2,f\left( x \right) > 0,\forall x \in \mathbb{R}\).
Cho hai đường thẳng \({\Delta _1}:4x - 5y + 8 = 0\) và \({\Delta _2}:10x + 8y - 4 = 0\).
a) Vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) lần lượt là \(\overrightarrow {{n_1}} = \left( {4; - 5} \right),\overrightarrow {{n_2}} = \left( { - 5; - 4} \right)\).
b) Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) vuông góc với nhau.
c) Góc giữa hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) nhỏ hơn 60 độ.
d) Điểm \(M\) thuộc giao điểm của \({\Delta _1}\) và trục hoành. Khoảng cách từ điểm \(M\) đến \({\Delta _2}\) là \(d\left( {M,{\Delta _2}} \right) = \frac{a}{{\sqrt b }}\left( {a,b \in \mathbb{Z}} \right)\) sao cho \(a,b\) là phân số tối giản. Khi đó \(\sqrt {a + b} > 7\).
Phương tình \(\sqrt {2{x^2} + 7x + 1} = \sqrt {3{x^2} + 4x - 9} \) có tổng các nghiệm là bao nhiêu?
Trong mặt phẳng \(Oxy\), cho hyperbol \(\left( H \right):\frac{{{x^2}}}{{32}} - \frac{{{y^2}}}{{{b^2}}} = 1\) (trong đó \(b > 0\) là hằng số). Biết rằng hypebol \(\left( H \right)\) đi qua điểm \(M\left( {8; - 3} \right)\). Tìm giá trị của \(b\).
Một công ty du lịch thông báo giá tiền cho chuyến đi tham quan của môt nhóm khách như sau 50 khách đầu tiên có giá 300000 đồng/người. Nếu có nhiều hơn 50 người đăng kí thì cứ có thêm một người, giá vé sẽ giảm 5000 đồng/người cho toàn bộ hành khách. Biết chi phí thực sự của chuyến đi là 15 080 000 đồng. Số người của nhóm khách du lịch nhiều nhất là bao nhiêu để công ty không bị lỗ.
Một vật chuyển động tròn đều chịu tác động của lực hướng tâm, quỹ đạo chuyển động của vật trong mặt phẳng tọa độ \(Oxy\) là đường tròn có phương trình \({x^2} + {y^2} = 100\). Vật chuyển động đến điểm \(M\left( {8;6} \right)\) thì bị bay ra ngoài. Trong những giây đầu tiên sau khi vật bay ra ngoài, vật chuyển động trên đường thẳng là tiếp tuyến của đường tròn. Biết phương trình tiếp tuyến đó có dạng \(ax + by - c = 0\) với \(a,b,c\) là các số nguyên dương và \(a,b\) nguyên tố cùng nhau. Giá trị của \(a + b + c\) bằng bao nhiêu?
Cho biểu thức \(f\left( x \right) = {x^2} + x - 42\). Hỏi \(x = 4\) có là nghiệm của phương trình \(\sqrt {f\left( x \right)} = \sqrt {2x - 30} \) không?
Trong mặt phẳng gắn hệ trục tọa độ \(Oxy\), hai tàu chuyển động đều, cùng xuất phát từ điểm \(O\). Sau 2 giờ, tàu một di chuyển đến vị trí điểm \(B\left( {15;20} \right)\), tàu hai di chuyển đến vị trí điểm \(C\left( {30; - 40} \right)\) (đơn vị trục tọa độ là km, kết quả làm tròn đến hàng phần trăm). Khoảng cách giữa hai tàu sau 2 giờ là bao nhiêu km? (kết quả làm tròn đến hàng phần trăm).
Trong mặt phẳng \(Oxy\), cho điểm \(M( - 1;2)\)và 2 đường thẳng\({d_1}:x + 2y + 1 = 0;\,{d_2}:2x + y + 2 = 0\). Viết phương trình đường thẳng \(\Delta \) qua \(M( - 1;2)\)và cắt \({d_1},{d_2}\) lần lượt tại \(A,B\)sao cho \(MA = 2MB\).








