Đề kiểm tra Giá trị lượng giác của góc lượng giác (có lời giải) - Đề 3
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cung có số đo \[250^\circ \] thì có số đo theo đơn vị radian là:
\[\frac{{25\pi }}{{12}}\].
\[\frac{{25\pi }}{{18}}\].
\[\frac{{25\pi }}{9}\].
\[\frac{{35\pi }}{{18}}\].
Trên đường tròn bán kính bằng 5, cho một cung tròn có độ dài bằng 10. Số đo rađian của cung tròn đó là
\(2\).
\(3\).
\(1\).
\(4\).
Một đường tròn có bán kính 30cm. Tính độ dài của cung tròn trên đường tròn đó có số đo \(2,5\).
\(7,5cm\).
\(0,83cm\).
\(75cm\).
\(12cm\).
Trong các hệ thức sau đây, hệ thức nào đúng?
\({\sin ^2}x + {\cos ^2}x = 1\).
\(\sin {x^2} + \cos {x^2} = 1\).
\(\sin 2x + \cos 2x = 1\).
\({\sin ^2}x + \cos {x^2} = 1\).
Cho \(\frac{{7\pi }}{4} < \alpha < 2\pi \).Xét câu nào sau đây đúng?
\(\cos \alpha > 0\).
\(\sin \alpha > 0\).
\(\tan \alpha > 0\).
\(\cot \alpha > 0\).
Cho \(0 < \alpha < \frac{\pi }{2}.\) Khẳng định nào sau đây đúng?
\(\tan \alpha > 0,\cot \alpha > 0.\)
\(\tan \alpha > 0,\cot \alpha < 0.\)
\(\tan \alpha < 0,\cot \alpha < 0.\)
\(\tan \alpha < 0,\cot \alpha > 0.\)
Đơn giản biểu thức \(A = \cos \left( {\alpha - \frac{\pi }{2}} \right)\), ta được:
\[\cos \alpha \].
\[\sin \alpha \].
\[--\cos \alpha \].
\[ - \sin \alpha \].
Giá trị của biểu thức \(S = 3 - {\sin ^2}90^\circ + 2{\cos ^2}60^\circ - 3{\tan ^2}45^\circ \) bằng
\(\frac{1}{2}\).
\( - \frac{1}{2}\).
\(1\).
\(3\)
Cho \(a\) là số thực bất kỳ. Chọn khẳng định đúng trong các khẳng định sau:
\[\sin a + \cos a = 1\].
\[{\sin ^3}a + {\cos ^3}a = 1\].
\[{\sin ^4}a + {\cos ^4}a = 1\].
\[{\sin ^2}a + {\cos ^2}a = 1\].
Các đẳng thức nào sau đây đồng thời xảy ra?
\(\sin \alpha = \frac{{\sqrt 2 }}{3}\);\[{\rm{cos}}\alpha {\rm{ = }}\frac{{\sqrt 5 }}{3}\].
\(\sin \alpha = \frac{{\sqrt 2 }}{5}\);\[{\rm{cos}}\alpha {\rm{ = }}\frac{{\sqrt 5 }}{5}\].
\(\sin \alpha = \frac{4}{5}\);\[{\rm{cos}}\alpha {\rm{ = }}\frac{{ - 3}}{5}\].
\(\sin \alpha = \frac{{\sqrt 3 }}{4}\);\[{\rm{cos}}\alpha {\rm{ = }}\frac{1}{4}\].
Cho \(\tan \alpha = \frac{1}{2}\). Giá trị của biểu thức \(P = \frac{{\sin \alpha }}{{2{{\sin }^3}\alpha + 3{{\cos }^3}\alpha }}\) là
\(\frac{5}{{26}}\).
\(\frac{1}{3}\).
\( - \frac{5}{{26}}\).
\( - \frac{1}{3}\).
Cho góc \(\alpha \) thỏa \({\rm{cot}}\alpha = \frac{3}{4}\) và \({0^O} < \alpha < {90^O}.\) Khẳng định nào sau đây đúng?
\[{\rm{cos}}\alpha = \frac{4}{5}\].
\(\sin \alpha = \frac{4}{5}\).
\({\rm{sin}}\alpha = - \frac{4}{5}\).
\[{\rm{cos}}\alpha = - \frac{4}{5}\].
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.Đổi số đo các góc sang đơn vị radian:
a)
b)
c)
d)
Tính được các giá trị lượng giác của góc \(\alpha = \frac{\pi }{3} + k2\pi \)(biết \(k \in \mathbb{Z}\)). Khi đó:
a) \(\sin \alpha = - \frac{{\sqrt 3 }}{2}\)
b) \(\cos \alpha = - \frac{1}{2}\)
c) \(\tan \alpha = \sqrt 3 \)
d) \(\cot \alpha = - \frac{{\sqrt 3 }}{3}\)
Tính được các giá trị lượng giác còn lại của góc \(x\), biết: \(\sin x = - \frac{3}{5}\) với \(\pi < x < \frac{{3\pi }}{2}\). Khi đó:
Cho \(\cot x = 2\). Tính được các biểu thức \({B_1} = \frac{{2\sin x + 3\cos x}}{{3\sin x - 2\cos x}},{B_2} = \frac{2}{{{{\cos }^2}x - \sin x\cos x}}\), khi đó:
a) Vì \(\cot x = 2\) nên \(\sin x \ne 0\).
b) \({B_1} = - 8\)
c) \({B_2} = - 5\)
d) \({B_1} + {B_2} = - 13\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
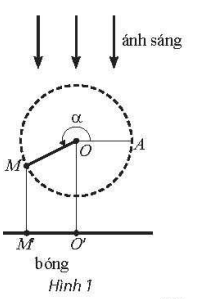
Thanh \(OM\) quay ngược chiều kim đồng hồ quanh gốc \(O\) của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như hình bên. Vị trí ban đầu của thanh là \(OA\). Hỏi độ dài bóng \(O'M\) của \(OM\) khi thanh quay được \(\frac{{60}}{{13}}\) vòng là bao nhiêu, biết độ dài thanh \(OM\) là \(10{\rm{\;cm}}\)? Kết quả làm tròn đến hàng phần mười.
Độ dài của ngày từ lúc Mặt Trời mọc đến lúc Mặt Trời lặn ở một thành phố \(X\) trong ngày thứ \(t\) của năm được tính xấp xỉ bởi công thức \(d\left( t \right) = 4{\rm{sin}}\left[ {\frac{{2\pi }}{{365}}\left( {t - 80} \right)} \right] + 12{\rm{\;}}\left( {t \in \mathbb{Z}{\rm{\;v\`a \;}}1 \le t \le 365} \right).\)
Thành phố \(X\) vào ngày 31 tháng 1 có bao nhiêu giờ có Mặt Trời chiếu sáng? Làm tròn kết quả đến hàng phần mười.
Một vệ tinh được định vị tại vị trí \(A\) trong không gian. Từ vị trí \(A\), vệ tinh bắt đầu chuyển động quanh Trái Đất theo quỹ đạo là đường tròn với tâm là tâm \(O\) của Trái Đất. Giả sử vệ tinh chuyển động hết một vòng của quỹ đạo trong \(2{\rm{\;h}}\) theo chiều kim đồng hồ. Khi vệ tinh chuyển động được \(3{\rm{\;h}}\), bán kính của vòng quay quét một góc lượng giác có số đo bằng bao nhiêu? (Tính theo đơn vị radian).
Một vòng quay Mặt Trời quay mỗi vòng khoảng 15 phút. Tại vị trí quan sát, bạn Linh thấy vòng quay chuyển động theo chiều kim đồng hồ. Khi vòng quay chuyển động được 10 phút, bán kính của vòng quay quét một góc lượng giác có số đo bằng bao nhiêu? (Tính theo đơn vị radian).
Bánh xe của người đi xe đạp quay được 12 vòng trong 6 giây.
a) Tính góc (theo độ và rađian) mà bánh xe quay được trong 1 giây.
b) Tính quãng đường mà người đi xe đã đi được trong 1 phút, biết rằng đường kính bánh xe đạp là \(860{\rm{\;mm}}\).
Kim giờ dài \(6{\rm{\;cm}}\) và kim phút dài \(11{\rm{\;cm}}\) của đồng hồ chỉ 4 giờ. Hỏi thời gian ít nhất để 2 kim vuông góc với nhau là bao nhiêu? Lúc đó tổng quãng đường hai đầu mút kim giờ và kim phút đi được là bao nhiêu?








