Đề kiểm tra Giá trị lượng giác của góc lượng giác (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Đổi số đo góc \({105^{\rm{o}}}\) sang rađian bằng
\(\frac{{5\pi }}{{12}}.\)
\(\frac{{7\pi }}{{12}}.\)
\(\frac{{9\pi }}{{12}}\)
\(\frac{{5\pi }}{8}.\)
Cho đường tròn lượng giác gốc \(A\) và điểm \(M\)nằm trên đường tròn lượng giác sao cho \[\widehat {MOx}\, = \,\widehat {MOy}\, = \,{45^o}\]. Mệnh đề nào sau đây đúng?
.
.
.
.
Góc có số đo \[{120^0}\] đổi sang rađian là
\(\frac{{2\pi }}{3}\).
\(\frac{{3\pi }}{2}\).
\(\frac{\pi }{4}\).
\(\frac{\pi }{{10}}\).
Cho đường tròn có bán kính \(6\) cm. Tìm số đo (rad) của cung có độ dài \(3\) cm.
\(1\).
\(0,5\).
\(2\).
\(3\).
Một bánh xe có \[72\] răng. Số đo góc mà bánh xe đã quay được khi di chuyển \[10\] răng là
\[30^\circ \].
\[40^\circ \].
\[50^\circ \].
\[60^\circ \].
Bánh xe đạp có đường kính \(55\,{\rm{cm}}\) ( kể cả lốp). Nếu chạy với vận tốc \(40\,{\rm{km}}\,{\rm{/}}\,{\rm{h}}\) thì trong \(25\,{\rm{s}}\) bánh xe quay được số vòng gần bằng với kết quả nào dưới đây?
\(52\).
\(161\).
\(322\).
\(200\).
Tìm khẳng định sai? (với điều kiện các hệ thức đã xác định)
\(\tan \left( {\pi + \alpha } \right) = \tan \alpha \).
\(\cos \left( {\frac{\pi }{2} + \alpha } \right) = \sin \alpha \).
\(\cot \left( { - \alpha } \right) = - \cot \alpha \).
\(\sin \left( {\pi - \alpha } \right) = \sin \alpha \).
Cho góc \(\alpha \) thỏa mãn \(2\pi < \alpha < \frac{{5\pi }}{2}\). Khẳng định nào sau đây sai?
\(\tan \alpha < 0\).
\(\cot \alpha > 0\).
\(\sin \alpha > 0\).
\(\cos \alpha > 0\).
Cho \(\frac{\pi }{2} < \alpha < \pi \). Kết quả đúng là
\(\sin \alpha > 0,\)\[\cos \alpha > 0\].
\(\sin \alpha < 0,\)\[\cos \alpha < 0\].
\(\sin \alpha > 0,\)\[\cos \alpha < 0\].
\(\sin \alpha < 0,\)\[\cos \alpha > 0\].
Cho \(0 < \alpha < \frac{\pi }{2}\). Mệnh đề nào sau đây sai?
\(\sin (\alpha \, + \,\pi ) < 0\).
\(\cos (\alpha \, + \,\pi ) > 0\).
\(\tan (\pi \, - \,\alpha ) > 0\).
\(\cot (\pi \, - \,\alpha ) < 0\).
Trong các đẳng thức sau, đẳng thức nào đúng?
\[\cos 150^\circ = \frac{{\sqrt 3 }}{2}\].
\[\cot 150^\circ = \sqrt 3 \].
\[\tan 150^\circ = - \frac{1}{{\sqrt 3 }}\].
\[\sin 150^\circ = - \frac{{\sqrt 3 }}{2}\].
Giá trị của \[\tan \frac{\pi }{6}\] là
\[\frac{{\sqrt 3 }}{3}\].
\[ - \frac{{\sqrt 3 }}{3}\].
\[\sqrt 3 \].
\[ - \sqrt 3 \].
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Tính được giá trị các biểu thức. Khi đó:
a)
b)
c) \(C = 2\sin \frac{\pi }{6} + \sqrt 3 \cos \frac{\pi }{6} = \frac{5}{2}\)
d) \(D = \frac{{\tan \frac{\pi }{4} + 1}}{{\frac{1}{{\sqrt 2 }}\cot \frac{\pi }{2} - 2}} = \frac{6}{5}\).
Cho . Xét được dấu của các biểu thức sau. Khi đó:
a)
b)
c)
d)
Cho \(\tan x = - 2\). Tính được các biểu thức \({A_1} = \frac{{5\cot x + 4\tan x}}{{5\cot x - 4\tan x}},{A_2} = \frac{{2\sin x + \cos x}}{{\cos x - 3\sin x}}\), khi đó:
a) \(\cot x = - \frac{1}{2}\)
b) Vì \(\tan x = - 2\) nên \(\cos x = 0\)
c) \({A_1} = - \frac{{21}}{{11}}\)
d) \({A_2} = \frac{3}{7}\)
Từ một vị trí ban đầu trong không gian, vệ tinh \(X\) chuyển động theo quỹ đạo là một đường tròn quanh Trái Đất và luôn cách tâm Trái Đất một khoảng bằng \(9200\;km\). Sau 2 giờ thì vệ tinh \(X\) hoàn thành hết một vòng di chuyển.
a) Quãng đường vệ tinh \(X\) chuyển động được sau 1 giờ là: \( \approx 28902,65(\;km){\rm{. }}\)
b) Quãng đường vệ tinh \(X\) chuyển động được sau 1,5 giờ là: \( \approx 43353,98(\;km)\)
c) Sau khoảng 5,3 giờ thì \(X\) di chuyển được quãng đường \(240000\;km\)
d) Giả sử vệ tinh di chuyển theo chiều dương của đường tròn, sau 4,5 giờ thì vệ tinh vẽ nên một góc \(\frac{{9\pi }}{2}\)rad?
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một đồng hồ treo tường, kim giờ dài \(10,57\;cm\) và kim phút dài \(13,34\;cm\). Trong 30 phút mũi kim giờ vạch lên cung tròn có độ dài bằng bao nhiêu?
Một chiếc đồng hồ có kim giờ và kim phút được cho như trong hình vẽ sau. Xét tia \(Ou\) là kim giờ, \(Ov\) là kim phút. Xét chiều quay của góc là chiều kim đồng hồ, hãy viết công thức số đo tổng quát của góc lượng giác \((Ou,Ov)\) trong trường hợp sau:
Một bánh xe có đường kính kể cả lốp xe là \(55\;cm\). Nếu xe chạy với tốc độ \(50\;km/h\) thì trong một giây bánh xe quay được bao nhiêu vòng? (Kết quả được làm tròn đến hàng phần trăm).
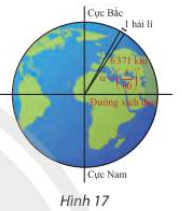
Hải lí là một đơn vị chiều dài hàng hải, được tính bằng độ dài một cung chắn một góc \(\alpha = {\left( {\frac{1}{{60}}} \right)^ \circ }\) của đường kinh tuyến (Hình 17). Đồi số đo \(\alpha \) sang radian và cho biết 1 hải lí bằng khoảng bao nhiêu kilômét, biết bán kính trung bình của Trái Đất là \(6371{\rm{\;km}}\). Làm tròn kết quả đến hàng phần trăm.
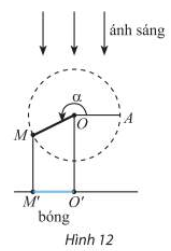
Thanh \(OM\) quay ngược chiều kim đồng hồ quanh trục\(O\)của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như Hình 12. Vị trí ban đầu của thanh là \(OA\). Hỏi độ dài bóng\(O'M\)của \(OM\)khi thanh quay được \(3\frac{1}{{10}}\) vòng là bao nhiêu, biết độ dài thanh\(OM\)là \(15{\rm{\;cm}}\)? Kết quả làm tròn đến hàng phần mười.
Khi xe đạp di chuyển, van \(V\)của bánh xe quay quanh trục \(O\) theo chiều kim đồng hồ với tốc độ góc không đổi là \(11{\rm{ rad}}/{\rm{s}}\) (Hình 13). Ban đầu van nằm ở vị trí \(A\). Hỏi sau một phút di chuyển, khoàng cách từ van đến mặt đất là bao nhiêu, biết bán kính \(OA = 58{\rm{\;cm}}\)? Già sử độ dày của lốp xe không đáng kể. Kết quả làm tròn đến hàng phần mười.









