Đề kiểm tra cuối học kỳ 2 Toán 10 Chân trời sáng tạo có đáp án - Đề 2
38 câu hỏi
Giá trị x nào sau đây là nghiệm của phương trình \(\sqrt {2{x^2} + 3x - 5} = x + 1\)?
x = –3;
x = 2;
Cả A và B đều đúng;
Cả A và B đều sai.
Tập nghiệm của bất phương trình (2x – 5)(x + 2) ≥ x2 – 4 là:
[–2; 3);
(–∞; –2) ∪ (3; +∞).;
ℝ;
(–∞; –2] ∪ [3; +∞).
Bất phương trình nào sau đây là bất phương trình bậc hai một ẩn?
3x2 – 12x + 1 ≤ 0;
2x3 + 5 > 0;
x2 + x – 1 = 0;
–x + 7 > 0.
Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0). Khẳng định nào sau đây đúng?
Nếu ∆ > 0 thì f(x) luôn cùng dấu với hệ số a, ∀x ∈ ℝ;
Nếu ∆ < 0 thì f(x) luôn trái dấu với hệ số a, ∀x ∈ ℝ;
Nếu ∆ = 0 thì f(x) luôn cùng dấu với hệ số a, ∀x ∈ ℝ \ \(\left\{ { - \frac{b}{{2a}}} \right\}\);
Nếu ∆ < 0 thì f(x) luôn cùng dấu với hệ số b, ∀x ∈ ℝ.
Cho kiểu gen AaBb. Giả sử quá trình giảm phân tạo giao tử bình thường và không xảy ra đột biến. Sơ đồ hình cây biểu thị sự hình thành giao tử được biểu diễn như hình bên.
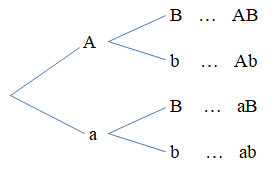
Từ sơ đồ cây, số loại giao tử của kiểu gen AaBb là:
4;
2;
8;
16.
Trong một hộp chứa 6 quả cầu trắng được đánh số từ 1 đến 6 và ba quả cầu đen được đánh số 7; 8; 9. Có bao nhiêu cách chọn một trong các quả cầu ấy?
27;
9;
6;
3.
Trên bàn có 8 cây bút chì khác nhau, 6 cây bút bi khác nhau và 10 cuốn tập khác nhau. Một học sinh muốn chọn một đồ vật duy nhất (một cây bút chì hoặc một cây bút bi hoặc một cuốn tập) thì số cách chọn khác nhau là:
24;
480;
48;
60.
Cho tập hợp X gồm n phần tử (n ≥ 1) và số nguyên k (1 ≤ k ≤ n). Một chỉnh hợp chập k của n phần tử là:
Một kết quả bất kì của sự sắp xếp k phần tử bất kì của tập hợp X;
Một kết quả của việc lấy k phần tử từ n phần tử của tập X và sắp xếp chúng theo một thứ tự nào đó;
Một số được tính bởi công thức: n(n – 1)(n – 2)…(n – k + 1);
Một kết quả của việc lấy k phần tử từ n phần tử của tập X.
Giá trị của \(A_{12}^4\) bằng:
12.11.10.9.8.7.6.5.4;
4.3.2.1;
12.11.10.9;
8!.
Trong một trường có 4 học sinh giỏi lớp 12, 3 học sinh giỏi lớp 11 và 5 học sinh giỏi lớp 10. Cần chọn 5 học sinh giỏi để tham gia một cuộc thi với các trường khác sao cho khối 12 có 3 em và mỗi khối 10, 11 có đúng 1 em. Vậy số tất cả các cách chọn là
60;
180;
330;
90.
Tổng số mũ của a và b trong mỗi hạng tử khi khai triển biểu thức (a + 2b)5 bằng
4;
5;
6;
7.
Số hạng chứa x3y trong khai triển \({\left( {xy + \frac{1}{y}} \right)^5}\) là:
3x3y;
5x3y;
10x3y;
4x3y.
Số hạng không chứa x trong khai triển \(P\left( x \right) = {\left( {{x^3} - \frac{1}{{{x^2}}}} \right)^5}\) (x ≠ 0) (theo chiều số mũ của x giảm dần) là số hạng thứ:
3;
6;
4;
5.
Tổng \(S = C_5^0 + 3C_5^1 + {3^2}C_5^2 + {3^3}C_5^3 + {3^4}C_5^4 + {3^5}C_5^5\) bằng:
S = 35;
S = 25;
S = 3.25;
S = 45.
Trong mặt phẳng tọa độ Oxy cho \(\overrightarrow a = \left( {3;4} \right)\). Độ dài của vectơ \(\overrightarrow a \) là:
\(\left| {\overrightarrow a } \right| = 5\);
\(\left| {\overrightarrow a } \right| = 3\);
\(\left| {\overrightarrow a } \right| = 7\);
\(\left| {\overrightarrow a } \right| = 1\).
Trong mặt phẳng tọa độ Oxy cho 2 điểm A(2; 5) và B(6; 7). Tọa độ C là trung điểm của AB là
C = (4; 6);
C = (5; 6);
C = (4; 5);
C = (5; 6);
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow {OA} = \left( {2;10} \right)\). Đâu là tọa độ của điểm A?
(0; 0);
(10; 2);
(‒ 10; ‒ 2);
(2; 10).
Trong mặt phẳng tọa độ Oxy cho 4 điểm A(1; 2), B(2; 3), C(1; ‒1) và D(4; 5). Khẳng định nào là đúng?
\(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng;
\(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) ngược hướng;
\(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) vuông góc với nhau;
\(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) tạo với nhau một góc 30°.
Phương trình tham số của đường thẳng nào sau đâycó vectơ chỉ phương \(\overrightarrow u = \left( {1;3} \right)?\)
\(\left\{ \begin{array}{l}x = t + 1\\y = 3t + 2\end{array} \right.\);
\(\left\{ \begin{array}{l}x = t + 1\\y = 2t + 3\end{array} \right.\);
\(\left\{ \begin{array}{l}x = t + 2\\y = t + 3\end{array} \right.\);
\(\left\{ \begin{array}{l}x = t + 3\\y = 2t + 1\end{array} \right.\).
Góc giữa 2 đường thẳng có thể có số đo nào sau đây?
135°;
67°;
91°;
180°.
Phương trình đường thẳng d có vectơ chỉ phương \(\overrightarrow u = \left( {1;3} \right)\) và đi qua điểm M(3; 4) là
3x – y – 5 = 0;
x + 3y – 15 =0;
x + 3y + 15 = 0;
3x – y + 15 = 0.
Đường thẳng d đi qua 2 điểm A(1; 3) và B(2; 5). Viết phương trình đoạn chắn của đường thẳng d.
\(\frac{x}{{ - \frac{1}{2}}} - \frac{y}{1} = 1\);
\(\frac{x}{{ - 2}} + \frac{y}{1} = 1\);
\(\frac{x}{{ - \frac{1}{2}}} + \frac{y}{1} = 1\);
\(\frac{x}{2} + \frac{y}{1} = 1\).
Phương trình tiếp tuyến của đường tròn tâm I(a; b) tại điểm M(x0; y0) nằm trên đường tròn có dạng:
(a – x0)(x – x0) – (b – y0)(y – y0) = 0;
(a – x0)(x – x0) + (b – y0)(y – y0) = 0;
(a + x0)(x – x0) – (b + y0)(y – y0) = 0;
(a + x0)(x – x0) + (b + y0)(y – y0) = 0.
Tiếp tuyến của đường tròn có tính chất nào sau đây?
Cắt đường tròn tại 2 điểm phân biệt;
Tiếp tuyến có vectơ chỉ phương là vectơ nối giữa tâm và tiếp điểm;
Tiếp tuyến có vectơ pháp tuyến là vectơ nối giữa tâm và tiếp điểm;
Cả A, B, C đều đúng.
Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?
x2 + y2 + 2x – 4y + 9 = 0;
x2 + y2 – 6x + 4y + 13 = 0;
2x2 + 2y2 – 8x – 4y + 2 = 0;
5x2 + 4y2 + x – 4y + 1 = 0.
Cho phương trình Hypebol \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\). Độ dài trục thực của Hypebol đó là:
3;
4;
6;
8.
Đường chuẩn của Parabol y2 = 14x là:
\(x + \frac{7}{2} = 0;\)
\(x - \frac{7}{2} = 0;\)
\(x + 7 = 0;\)
\(x - 7 = 0.\)
Viết phương trình chính tắc của Elip có độ dài trục lớn và trục nhỏ lần lượt là 20 và 10.
\(\frac{{{x^2}}}{{20}} + \frac{{{y^2}}}{{10}} = 1\) ;
\(\frac{{{x^2}}}{{{{20}^2}}} + \frac{{{y^2}}}{{{{10}^2}}} = 1\);
\(\frac{{{x^2}}}{{{{10}^2}}} + \frac{{{y^2}}}{{{5^2}}} = 1\);
\(\frac{{{x^2}}}{{20}} + \frac{{{y^2}}}{{10}} = 0\).
Viết phương trình đường tròn tâm I đi qua 3 điểm A(1; 1), B(2; 3) và C(4; 6).
x2 + y2 – 5x + y + 26 = 0;
x2 + y2 – 4x + 17y + 26 = 0;
x2 + y2 – 45x + 17y + 26 = 0;
x2 + y2 – 5x + 27y + 56 = 0.
Một hoạt động mà ta không thể biết trước được kết quả của nó thì được gọi là:
Không gian mẫu;
Phép thử;
Phép thử ngẫu nhiên;
Cả B, C đều đúng.
Biến cố là:
Một hoạt động mà ta không thể biết trước được kết quả của nó;
Tập con của không gian mẫu;
Tập hợp tất cả các kết quả có thể có của phép thử ngẫu nhiên;
Một kết quả thuận lợi.
Cho 3 hộp, mỗi hộp đựng 5 cái thẻ được đánh số từ 1 đến 5. Rút ngẫu nhiên từ mỗi hộp một tấm thẻ. Biến cố nào sau đây là biến cố chắc chắn?
X: “Tổng các số ghi trên ba tấm thẻ rút ra đều lớn hơn hoặc bằng 3”;
Y: “Tổng các số ghi trên ba tấm thẻ rút ra không nhỏ hơn 4”;
Z: “Tổng các số ghi trên ba tấm thẻ rút ra bằng 8”;
T: “Tổng các số ghi trên ba tấm thẻ luôn lớn hơn 15”.
Xác suất của biến cố H được xác định bởi công thức:
P(H) = n(H);
\[P\left( H \right) = \frac{{n\left( \Omega \right)}}{{n\left( H \right)}}\];
P(H) = n(H).n(Ω);
\[P\left( H \right) = \frac{{n\left( H \right)}}{{n\left( \Omega \right)}}\].
Có ba chiếc hộp. Mỗi hộp chứa 5 tấm thẻ được đánh số từ 1 đến 5. Lấy ngẫu nhiên từ mỗi hộp một thẻ rồi cộng các số trên 3 tấm thẻ vừa rút ra lại với nhau. Xác suất để kết quả thu được là số chẵn là:
\(\frac{1}{6}\);
\(\frac{{99}}{{125}}\);
\(\frac{1}{2}\);
\(\frac{{26}}{{125}}\).
Xét các số tự nhiên gồm 5 chữ số khác nhau được lập từ các số 1; 3; 5; 7; 9. Xác suất để tìm được một số không có dạng \[\overline {135xy} \] là:
\(\frac{5}{6}\);
\(\frac{1}{{60}}\);
\(\frac{{59}}{{60}}\);
\(\frac{1}{6}\).
Trong mặt phẳng Oxy, cho hai điểm A(3; 1) và B(– 2; 4). Viết phương trình đường tròn (C) có tâm I thuộc trục hoành và đi qua hai điểm A, B.
Hai hộp chứa các quả cầu. Hộp thứ nhất chứa 3 quả đen và 2 quả trắng, hộp thứ hai chứa 4 quả đen và 6 quả trắng.
a) Lấy ngẫu nhiên từ hộp thứ nhất 1 quả. Tính xác suất để lấy được 1 quả đen.
b) Lấy ngẫu nhiên từ mỗi hộp một quả. Tính xác suất để lấy được 2 quả cùng màu.
Có 5 bưu thiếp khác nhau và 6 bì thư khác nhau. Cần chọn 3 bưu thiếp bỏ vào 3 bì thư, mỗi bì thư một bưu thiếp và gửi cho 3 người bạn mỗi bạn một bưu thiếp. Hỏi có mấy cách thực hiện?








