15 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Cho tam giác \(ABC\) có có \(a = 8\), \(c = 3\) và \(\widehat B = 60^\circ \). Độ dài cạnh \(b\) bằng
\(49\).
\(\sqrt {{\rm{97}}} \).
\(\sqrt {61} \).
\(7\).
Cho tam giác \(ABC\) có \(AB = 7\), \(AC = 8\) và \(\widehat A = 60^\circ \). Độ dài của cạnh \(BC\) bằng
\(7\).
\(47\).
\(\sqrt {57} \).
\(2\sqrt {57} \).
Cho \(\Delta ABC\) có \(AB = 13\,,\,\,AC = 8\) và \(BC = 7\). Tính số đo của góc \(\widehat {ACB}\).
\(30^\circ \).
\(90^\circ \).
\(60^\circ \).
\(120^\circ \).
Tam giác \(ABC\) có \(\widehat B = 60^\circ \), \(\widehat C = 45^\circ \) và \(AB = 3\). Tính độ dài cạnh \(AC\).
\(3\sqrt 6 \).
\(\frac{{3\sqrt 6 }}{2}\).
\(\sqrt 6 \).
\(\frac{{3\sqrt 6 }}{4}\).
Cho tam giác ABC có BC = a, AC = b, AB = c. Gọi p là nửa chu vi của tam giác, r là bán kính đường tròn nội tiếp tam giác và S là diện tích tam giác đó. Mệnh đề nào sau đây đúng?
\(S = p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)\).
\(S = 2bc\sin A\).
\(S = pr\).
\(S = \frac{{abc}}{{4r}}\).
Tam giác \(ABC\) có \(AB = 4\,,\,\,AC = 6\) và \(\widehat {BAC} = 30^\circ \). Tính diện tích tam giác \(ABC\).
\(6\).
\(3\).
\(6\sqrt 3 \).
\(3\sqrt 3 \).
Một tam giác có ba cạnh là 10, 12, 18. Diện tích tam giác bằng bao nhiêu?
\(42\sqrt 2 \).
\(40\sqrt 2 \).
\(40\sqrt 3 \).
\(41\sqrt 3 \).
Cho tam giác \(ABC\) có cạnh \(AB = 2\,{\rm{cm}}\), \(\widehat {ABC} = 60^\circ \) và \(\widehat {BAC} = 75^\circ \)(như hình vẽ bên dưới).
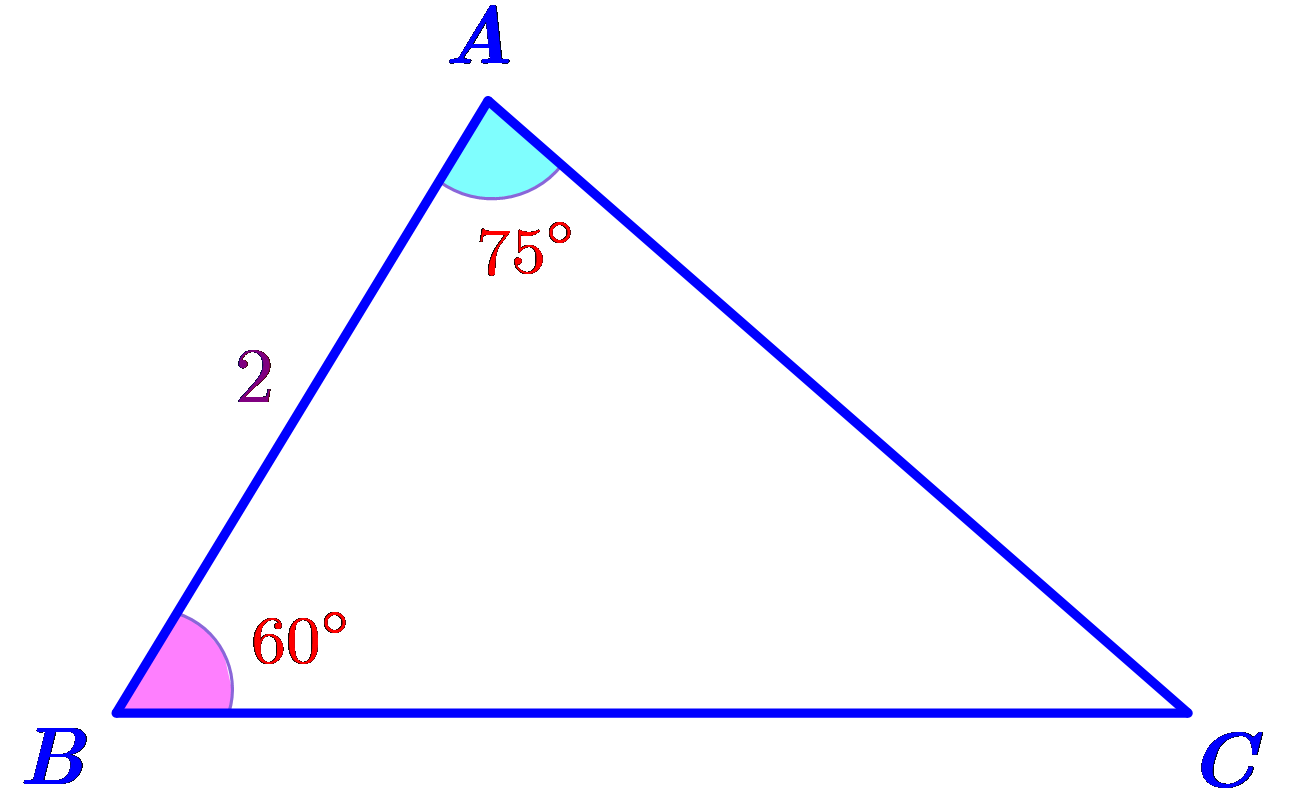
Diện tích tam giác \(ABC\) gần nhất với giá trị nào sau đây?
\(2,37\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
\(0,63\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
\(2,45\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
\(1,58\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Cho tam giác \(ABC\) biết \(\widehat B = 45^\circ \) và \(\widehat C = 60^\circ \). Tỉ số \(\frac{{AB}}{{AC}}\) bằng
\(\frac{{\sqrt 6 }}{2}\).
\(\frac{{\sqrt 6 }}{3}\).
\(\sqrt 6 \).
\(\frac{6}{5}\).
Cho tam giác nhọn \(ABC\) có \(\widehat A = 30^\circ \) và \(BC = 4\). Bán kính \(R\) của đường tròn ngoại tiếp tam giác \(ABC\) bằng
\[R = 2\].
\[R = 3\].
\[R = 4\].
\[R = 5\].
Cho tam giác ABC có BC = a, AC = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 3 lần và giảm cạnh AB đi 2 lần, đồng thời giữ nguyên góc B thì khi đó diện tích tam giác mới được tạo thành bằng
\[2S\].
\[\frac{3}{2}S\].
\[6S\].
\[\frac{2}{3}S\].
Cho tam giác \(ABC\) có \(AB = 3\), \(BC = 5\) và độ dài đường trung tuyến \(BM = \sqrt {13} \). Bán kính \(r\) của đường tròn nội tiếp \[\Delta ABC\] bằng
\(2\).
\(\frac{1}{2}\).
\(1\).
\(\sqrt 2 \).
Tam giác \[ABC\] có \[BC = 12\], \[CA = 9\] và \[AB = 6\]. Trên cạnh \[BC\] lấy điểm \[M\] sao cho \[BM = 8\]. Tính độ dài đoạn thẳng \[AM\].
\(34\).
\(17\).
\(\sqrt {34} \).
\(\sqrt {43} \).
Trên biển một con thuyền thả neo ở vị trí A. Một người đứng ở vị trí K trên bờ biển muốn đo khoảng cách từ người đó đến con thuyền, người đó đã chọn một điểm H trên bờ với K và đo được KH = 380 m, \(\widehat {AKH} = 50^\circ ,\widehat {AHK} = 45^\circ \). Khoảng cách KA từ người đó đến con thuyền bằng
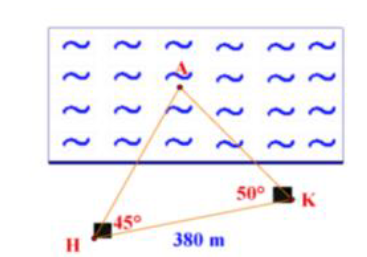
\(KA \approx 270\;{\rm{m}}\).
\(KA \approx 280\;{\rm{m}}\).
\(KA \approx 290\;{\rm{m}}\).
\(KA \approx 300\;{\rm{m}}\).
Cho tam giác ABC có AB = 5, AC = 8 và \(\widehat {BAC} = 60^\circ \). Khi đó, bán kính đường tròn nội tiếp tam giác ABC bằng
\(1\).
\(2\).
\(\sqrt 3 \).
\(2\sqrt 3 \).
