10 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Tính \(\cos 150^\circ \).
\(\frac{1}{2}\).
\[\frac{{\sqrt 3 }}{2}\].
\( - \frac{1}{2}\).
\( - \frac{{\sqrt 3 }}{2}\).
Cho hình bình hành \(ABCD\) như hình vẽ bên dưới. Biết rằng \(\cos \alpha = \frac{3}{5}\). Khi đó \(\cos \beta \) bằng
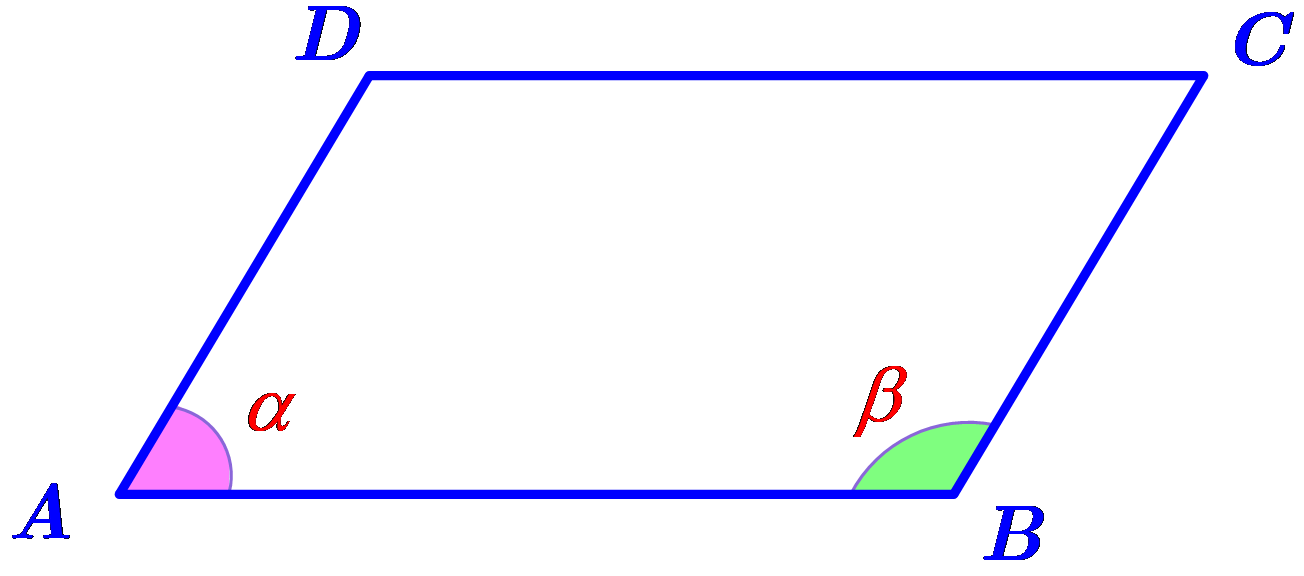
\(\frac{2}{5}\).
\[ - \frac{3}{5}\].
\(\frac{4}{5}\).
\(\frac{3}{5}\).
Cho góc \(90^\circ < \alpha < 180^\circ \). Biết rằng \(\sin \alpha = \frac{1}{3}\). Tính giá trị của \(\cos \alpha \).
\(\cos \alpha = \frac{2}{3}\).
\(\cos \alpha = - \frac{2}{3}\).
\(\cos \alpha = \frac{{2\sqrt 2 }}{3}\).
\(\cos \alpha = \frac{{ - 2\sqrt 2 }}{3}\).
Biết rằng điểm \(M\left( {a\,;\,b} \right)\) thoả mãn \[\widehat {MOx} = 30^\circ \] (hình vẽ minh hoạ). Khi đó giá trị của \(a\) bằng
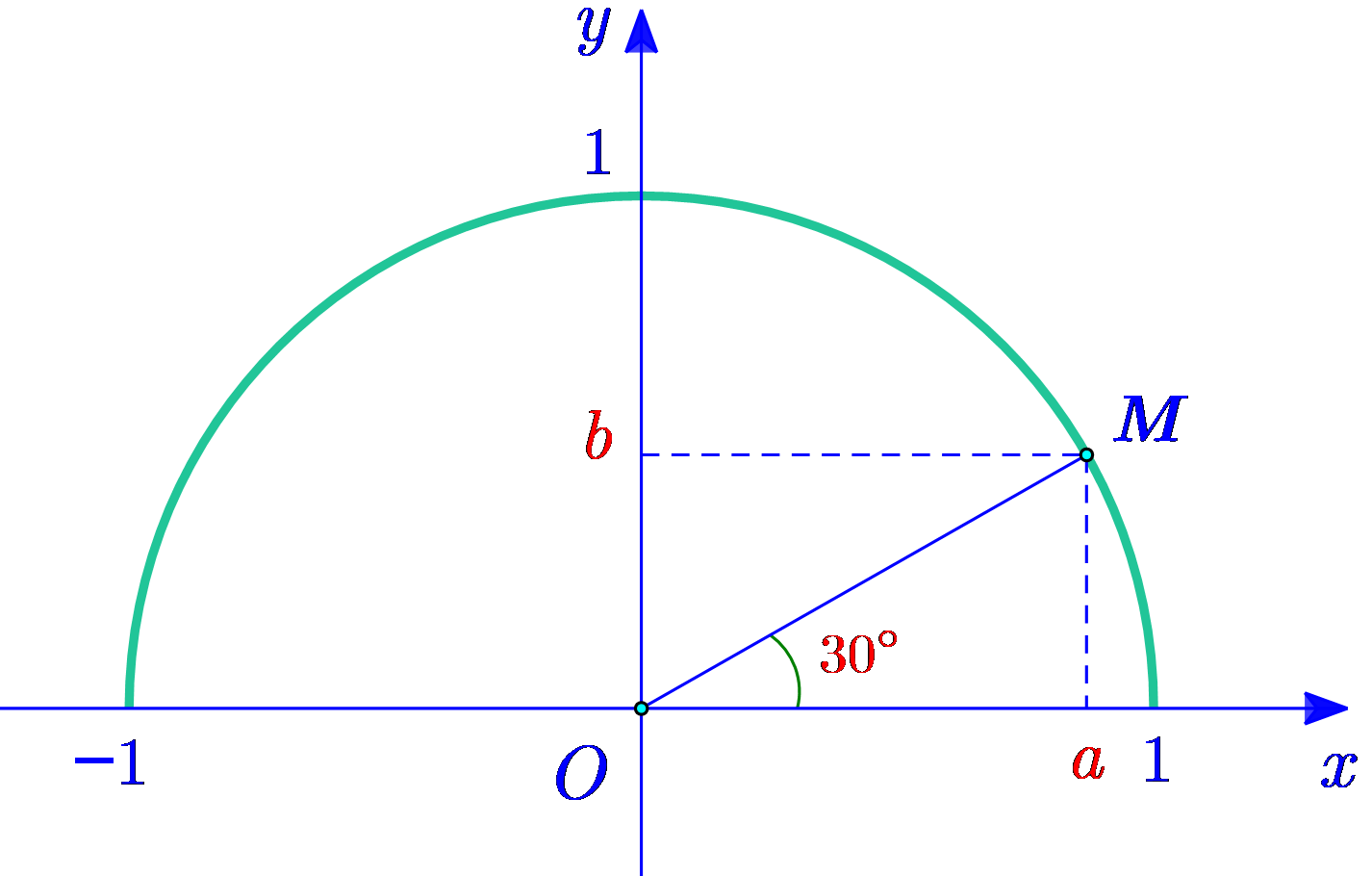
\(\frac{3}{5}\).
\(\frac{1}{2}\).
\(\frac{{\sqrt 3 }}{2}\).
\(\frac{4}{5}\).
Cho 2 góc nhọn \(\alpha \) và \(\beta \) thoả mãn \(\alpha + \beta = 90^\circ \). Đẳng thức nào sau đây sai?
\(\sin \alpha = \cos \beta \).
\(\cos \alpha = - \sin \beta \).
\(\tan \alpha = \cot \beta \).
\(\cot \alpha = \tan \beta \).
Cho góc \(\alpha \) thoả mãn \(\sin \alpha = \frac{3}{5}\) và \(0^\circ < \alpha < 90^\circ \). Khi đó giá trị \(\cot \left( {180^\circ - \alpha } \right)\) bằng
\[\frac{4}{3}\].
\[\frac{3}{4}\].
\[ - \frac{4}{3}\].
\[ - \frac{3}{4}\].
Cho góc \(\alpha \) thỏa mãn \(0^\circ \le \alpha \le 180^\circ \). Khẳng định nào sau đây đúng?
\(\sin \left( {180^\circ - \alpha } \right) = \sin \alpha \).
\(\cos \left( {180^\circ - \alpha } \right) = \cos \alpha \).
\(\tan \left( {180^\circ - \alpha } \right) = \tan \alpha \).
\(\cot \left( {180^\circ - \alpha } \right) = \cot \alpha \).
Biết rằng \[\cos \alpha = \frac{1}{3}\]. Giá trị của biểu thức \(P = {\sin ^2}\alpha + 3{\cos ^2}\alpha \) là
\[\frac{1}{3}\].
\[\frac{{10}}{9}\].
\[\frac{{11}}{9}\].
\[\frac{4}{3}\].
Cho góc \(\alpha \) thỏa mãn \(\tan \alpha = 4\). Tính giá trị của biểu thức \[A = \frac{{\sin \alpha + \cos \alpha }}{{\sin \alpha - 3\cos \alpha }}\].
\(A = 1\).
\(A = \frac{1}{2}\).
\(A = \frac{1}{5}\).
\(A = 5\).
Kết quả rút gọn của biểu thức \({\left( {\frac{{\sin \alpha + \tan \alpha }}{{\cos \alpha + 1}}} \right)^2} + 1\) bằng
\(2\).
\(1 + \tan \alpha \).
\(\frac{1}{{{{\cos }^2}\alpha }}\).
\(\frac{1}{{si{n^2}\alpha }}\).
