10 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Trong các cặp số \(\left( {x\,;y} \right)\) sau đây, cặp nào là nghiệm của bất phương trình \[2x + y < 1\]?
\[\left( { - 2\,;1} \right)\].
\[\left( {0\,;1} \right)\].
\[\left( {3\,;7} \right)\].
\[\left( {2\,; - 1} \right)\].
Cặp số \[\left( {3\,;2} \right)\] không là nghiệm của bất phương trình nào sau đây?
\[x + y--3 > 0\].
\[--x--y < 0\].
\[x + 3y + 1 < 0\].
\[--x--3y--1 < 0\].
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
\(2{x^2} + 3{y^2} < 0\).
\(2xy - y > 0\).
\(2x + 3{y^2} > 0\).
\(2x + 3y < 0\).
Miền nghiệm của bất phương trình \[3x + 2\left( {y - 3} \right) \ge 4\left( {x - 2} \right) - y - 1\] là nửa mặt phẳng chứa điểm nào sau đây?
\[\left( {2\,; - 2} \right)\].
\[\left( { - 3\,;1} \right)\].
\[\left( {4\,;0} \right)\].
\[\left( {0\,; - 2} \right)\].
Miền nghiệm của bất phương trình \(3x - 2y \ge - 6\) được biểu diễn bởi phần không gạch chéo trong hình nào được cho dưới đây ?
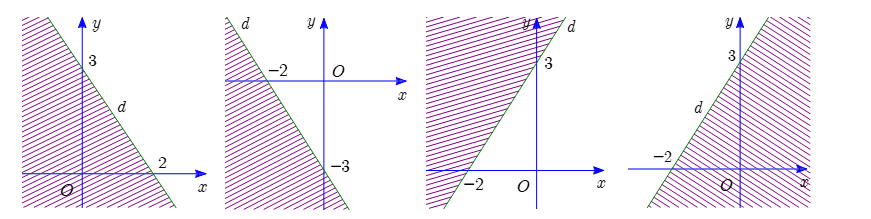
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Miền không bị gạch (không tính đường thẳng) được cho bởi hình sau là miền nghiệm của bất phương trình nào?

\[2x + y - 6 > 0\].
\[2x + y - 6 < 0\].
\[x + 2y - 6 < 0\].
\[x + 2y - 6 > 0\].
Phần không bị gạch (kể cả bờ) trong hình vẽ là miền nghiệm của bất phương trình nào sau đây?
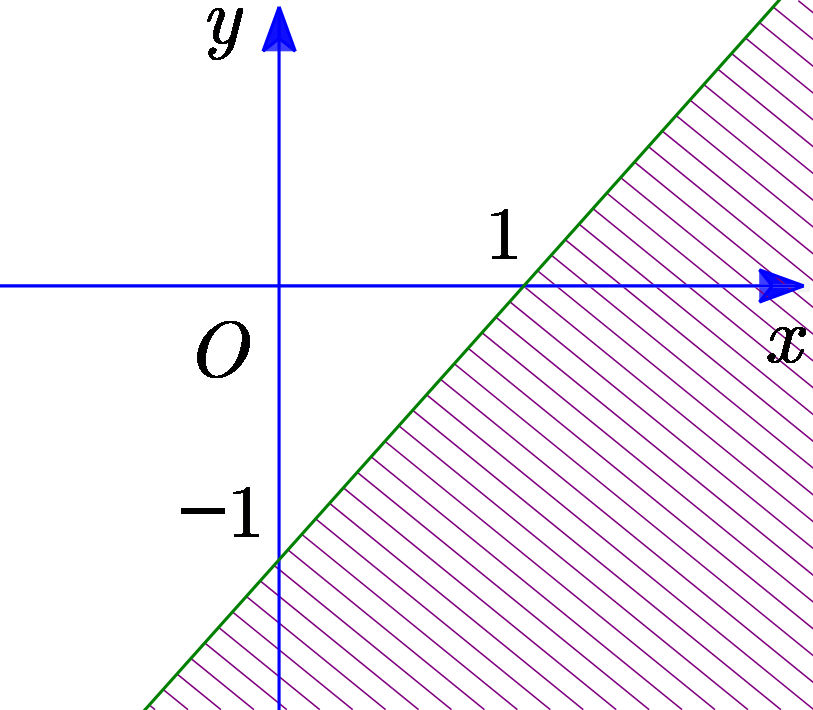
\(x + y > 1\).
\(x - y < 1\).
\(x + y \le 1\).
\(x - y \le 1\).
Bất phương trình nào sau đây có miền nghiệm được biểu diễn bởi phần không gạch sọc (tính cả biên) trong hình vẽ bên dưới?
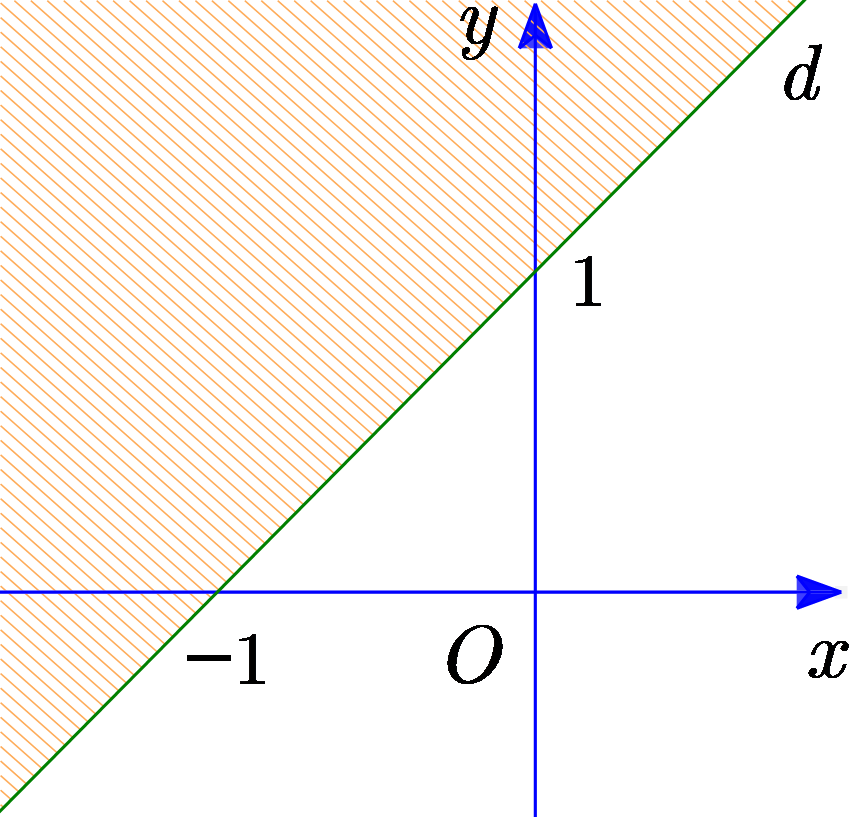
\(2x - y + 1 \le 0\).
\(2x - y + 1 > 0\).
\(x - y + 1 \ge 0\).
\(x - y + 1 < 0\).
Miền không gạch chéo (không kể bờ \(d\)) trong hình sau là miền nghiệm của bất phương trình nào trong các bất phương trình dưới đây?
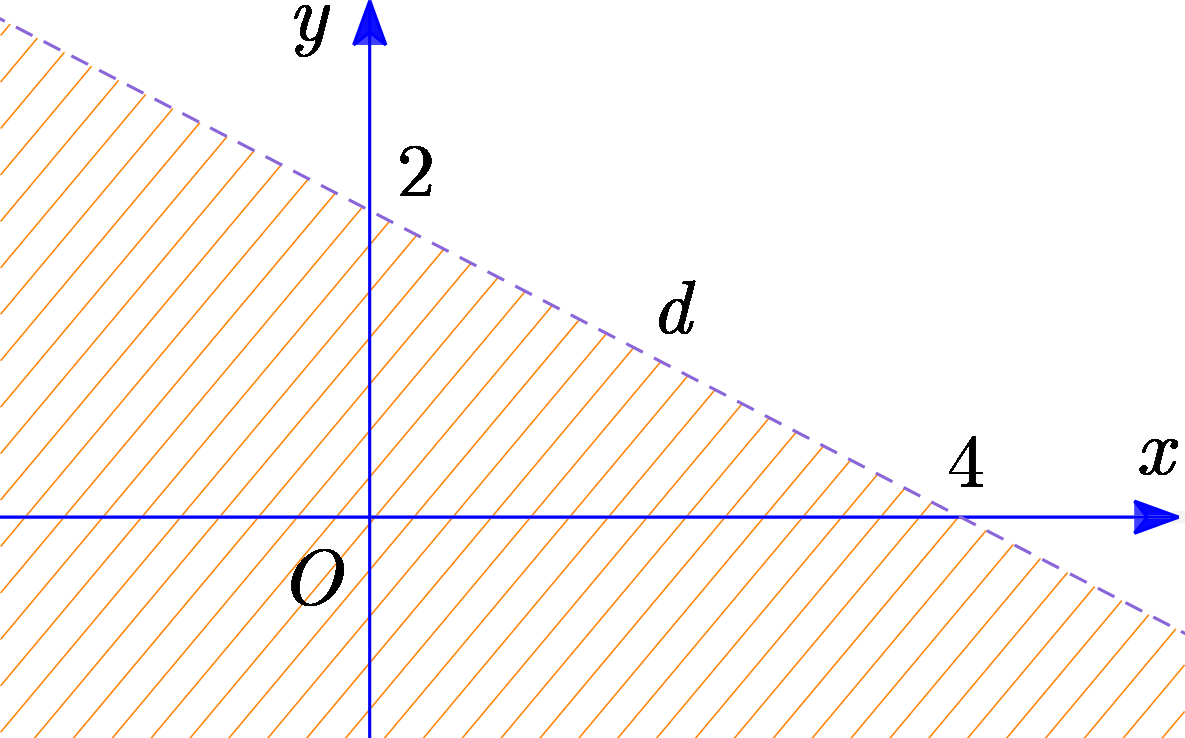
\[x + 2y < 4\].
\[2x + y \ge 4\].
\[x + 2y \ge 4\].
\[x + 2y > 4\].
Bạn Việt mang \(100\,000\) đồng ra chợ mua hoa cúc và hoa hồng. Một bông hoa cúc có giá \(3\,000\) đồng, một bông hoa hồng có giá \(6\,000\) đồng. Gọi \(x\) và \(y\) lần lượt là số bông hoa cúc và số bông hoa hồng bạn Việt mua. Bất phương trình bậc nhất hai ẩn \(x,\,\,y\) để biểu diễn số tiền Việt mua hoa cúc và hoa hồng là
\(3x + 6y \le 100\).
\(6x + 3y \le 100\).
\(3x + 6y \ge 100\).
\(6x + 3y \ge 100\).
