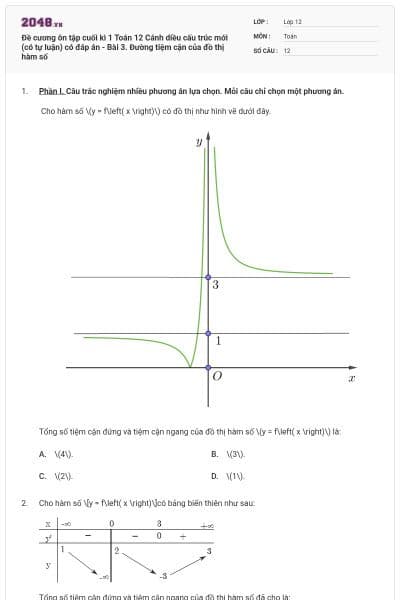
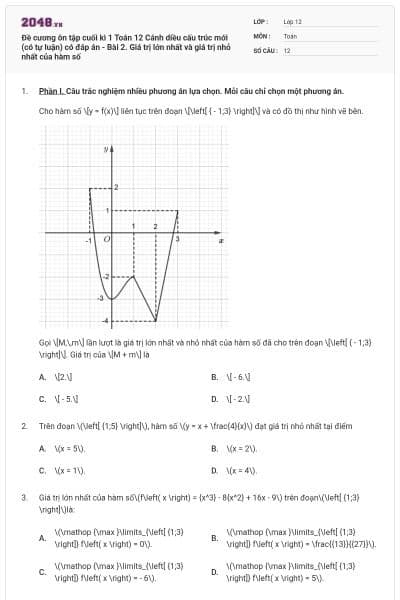
Đề cương ôn tập cuối kì 1 Toán 12 Cánh diều (có tự luận) có đáp án - Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
11 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
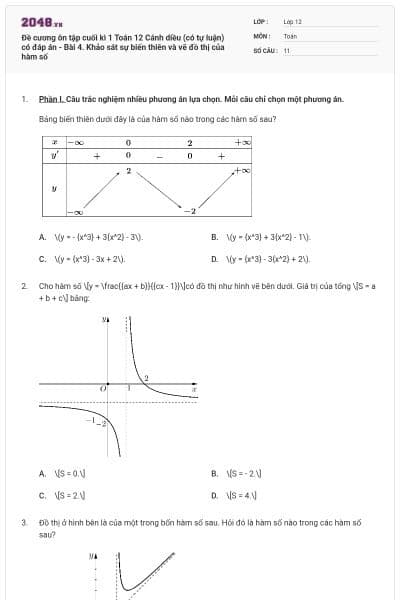
Bảng biến thiên dưới đây là của hàm số nào trong các hàm số sau?
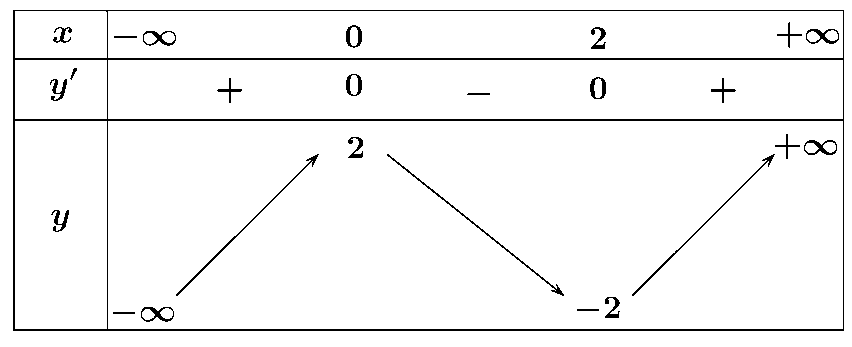
\(y = - {x^3} + 3{x^2} - 3\).
\(y = {x^3} + 3{x^2} - 1\).
\(y = {x^3} - 3x + 2\).
\(y = {x^3} - 3{x^2} + 2\).
Cho hàm số \[y = \frac{{ax + b}}{{cx - 1}}\]có đồ thị như hình vẽ bên dưới. Giá trị của tổng \[S = a + b + c\] bằng:
![Cho hàm số \[y = \frac{{ax + b}}{{cx - 1}}\] có đồ thị như hình vẽ bên dưới. Giá trị của tổng \[S = a + b + c\] bằng: A. \[S = 0.\] B. \[S = - 2.\] C. \[S = 2.\] D. \[S = 4.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/5-1761390678.png)
\[S = 0.\]
\[S = - 2.\]
\[S = 2.\]
\[S = 4.\]
Đồ thị ở hình bên là của một trong bốn hàm số sau. Hỏi đó là hàm số nào trong các hàm số sau?
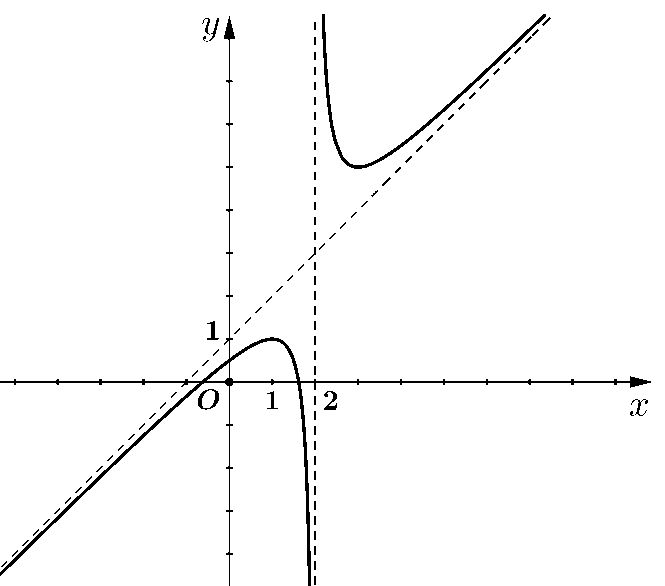
\[y = \frac{{{x^2} - x - 1}}{{x - 2}}\].
\[y = \frac{{{x^2} + x - 1}}{{x - 2}}\].
\[y = \frac{{{x^2} - 2x - 1}}{{x - 2}}\].
\[y = \frac{{{x^2} + x + 1}}{{x - 2}}\].
Đường cong hình bên là đồ thị hàm số \(y = {\rm{a}}{x^3} + b{x^2} + cx + d\).
![Đường cong hình bên là đồ thị hàm số \(y = {\rm{a}}{x^3} + b{x^2} + cx + d\). Xét các phát biểu sau: 1. \(a = - 1\) 2. \(ad < 0\) 3. \(ad > 0\) 4. \(d = - 1\) 5.\(a + c = b + 1\) Số phát biểu sai là: A. \[2\]. B. \[3\]. C. \[1\]. D. \[4\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/7-1761390753.png)
Xét các phát biểu sau:
1. \(a = - 1\)
2. \(ad < 0\)
3. \(ad > 0\)
4. \(d = - 1\)
5.\(a + c = b + 1\)
Số phát biểu sai là:
\[2\].
\[3\].
\[1\].
\[4\].
Cho hàm số \(y = \frac{{ax - 1}}{{cx + d}}\) có tiệm cận đứng \(x = 1\), tiệm cận ngang \(y = - 2\) và đi qua điểm \(A\left( {2; - 3} \right)\). Lúc đó hàm số \(y = \frac{{ax - 1}}{{cx + d}}\) là hàm số nào trong bốn hàm số sau:
\[y = \frac{{ - 3}}{5}.\frac{{2x + 1}}{{x - 1}}.\]
\(y = \frac{{2x - 1}}{{1 - x}}\).
\(y = \frac{{ - 2x - 1}}{{ - x + 1}}.\)
\(y = \frac{{2x - 1}}{{x - 1}}.\)
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Nhà máy\(A\) chuyên sản xuất một loại sản phẩm cho nhà máy\(B\). Hai nhà máy thỏa thuận rằng, hằng tháng \(A\) cung cấp cho \(B\) số lượng sản phẩm theo đơn đặt hàng của \(B\) (tối đa \(100\) tấn sản phẩm). Nếu số lượng đặt hàng là \(x\) tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm được biểu diễn bởi công thức: \(P\left( x \right) = 45 - 0,001{x^2}\) (triệu đồng). Cho phí để \(A\) sản xuất \(x\) tấn sản phẩm trong một tháng là \(C\left( x \right) = 100 + 30x\) triệu đồng (gồm \(100\)triệu đồng chi phí cố định và \(30\) triệu đồng cho mỗi tấn sản phẩm).
a) Chi phí để \(A\) sản xuất \(10\) tấn sản phẩm trong một tháng là \(400\)triệu đồng.
b) Số tiền \(A\) thu được khi bán \(10\) tấn sản phẩm cho \(B\) là \(600\)triệu đồng.
c) Lợi nhuận mà \(A\) thu được khi bán \(x\) tấn sản phẩm \(\left( {0 \le x \le 100} \right)\) cho \(B\) được biểu diễn bởi công thức \(H\left( x \right) = - 0,001{x^3} + 15x - 100\).
d) Bên \(A\) bán cho \(B\) khoảng \(70,7\) tấn sản phẩm mỗi tháng thì thu được lợi nhuận lớn nhất.
Cho hàm số \(y = \frac{{ - {x^2} - 3x + 4}}{{x - 3}}\) có đồ thị là \(\left( C \right)\).
a) Đồ thị \(\left( C \right)\) có tiệm cận xiên là \(y = - x - 6\).
b) Đồ thị \(\left( C \right)\) nhận giao điểm \(I\left( {3\,;\, - 9} \right)\) làm tâm đối xứng.
c) Đồ thị \(\left( C \right)\) có hai điểm cực trị nằm 2 phía đối với \(Oy\).
d) Đồ thị không cắt trục \(Ox\).
Cho hàm số \[y = f\left( x \right) = {x^3} - 6{x^2} - 15x + 20\].
a) Đồ thị hàm số \(y = f\left( x \right)\) cắt trục tung tại điểm có tung độ bằng \(20\).
b) Hàm số đồng biến trên khoảng \(\left( { - \infty \,;\, - 1} \right) \cap \left( {5\,;\, + \infty } \right)\).
c) Tâm đối xứng của đồ thị hàm số có toạ độ \(I\left( {2\,;\, - 26} \right)\).
d) Giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên khoảng \(\left( { - 4\,;\, + \infty } \right)\) bằng \( - 80\).
Phần III. Trắc nghiệm trả lời ngắn
Gọi \(S\) là tập hợp các giá trị \(m\) để tiệm cận xiên của đồ thị hàm số \(y = \frac{{m{x^2} + x - 3}}{{x - 1}}\) tạo với hai trục hệ tọa độ \(Oxy\) một tam giác có diện tích bằng \(2\). Khi đó tổng các giá trị của \(S\) bằng bao nhiêu?
Cho hàm số \(f\left( x \right) = \frac{{ax + 1}}{{bx + c}}\) \(\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:
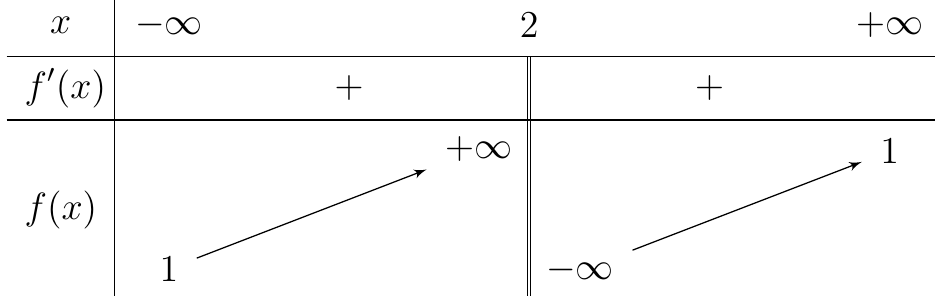
Trong các số \(a,b\) và \(c\) có bao nhiêu số dương?
Một chuyển động xác định bởi phương trình \(S\left( t \right) = a{t^3} + b{t^2} + ct + d\left( {a,b,c,d \in \mathbb{R}} \right)\) trong đó \(t\) tính bằng giây và \(S\) tính bằng mét. Biết rằng đồ thị của hàm số \(S\left( t \right)\) là đường cong như hình.
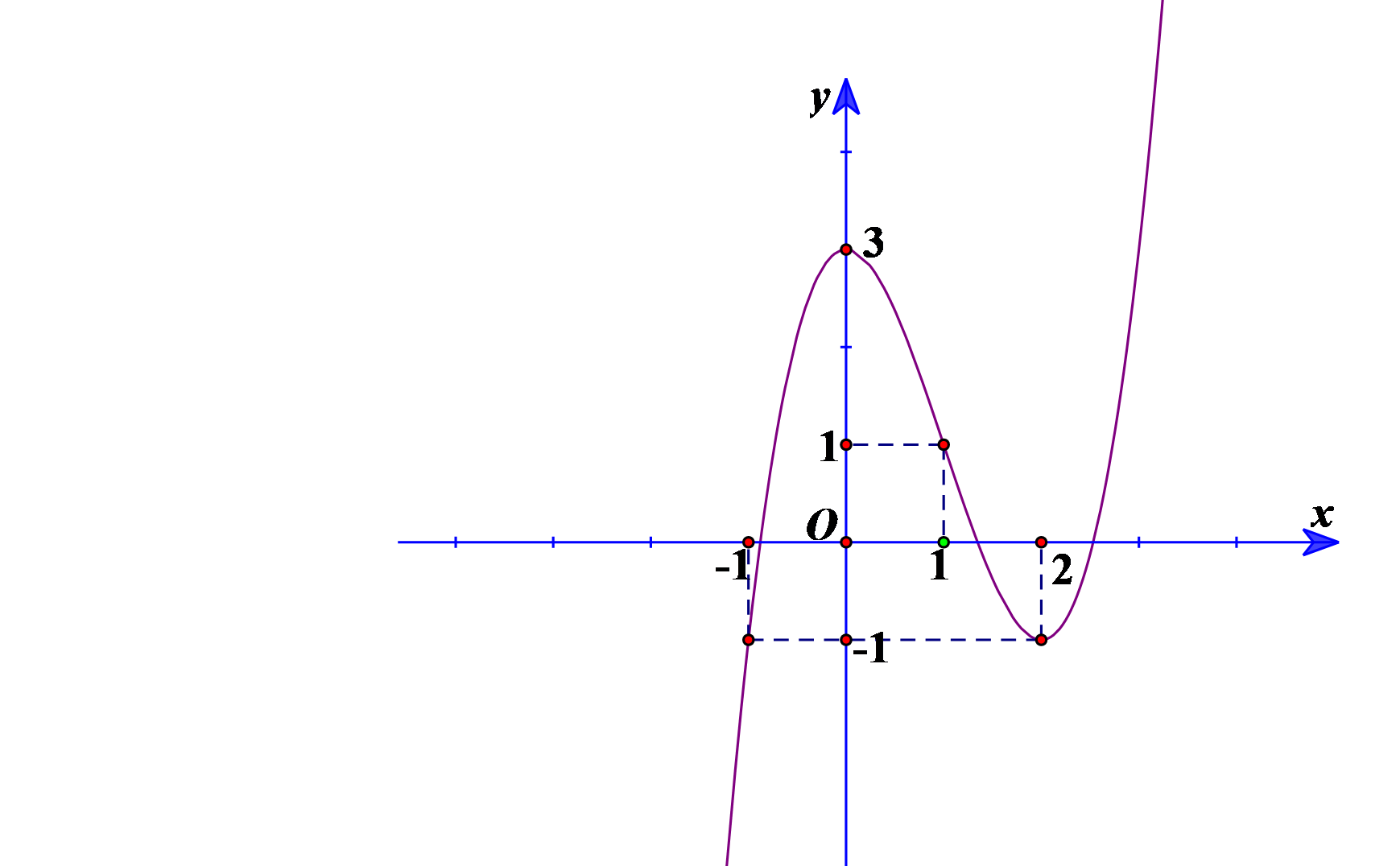
Tính vận tốc (m/s) của chuyển động tại thời điểm gia tốc bằng 12 m/s2.