Đề cương ôn tập cuối kì 1 Toán 12 Cánh diều (có tự luận) có đáp án - Bài 1. Vectơ và các phép toán vectơ trong không gian
12 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Trong không gian cho 3 điểm \[M,{\rm{ }}N,{\rm{ }}P\] phân biệt. Tính \(\overrightarrow {PM} + \overrightarrow {MN} \).
\[\overrightarrow {NM} \].
\[\overrightarrow {MN} \].
\[\overrightarrow {NP} \].
\[\overrightarrow {PN} \].
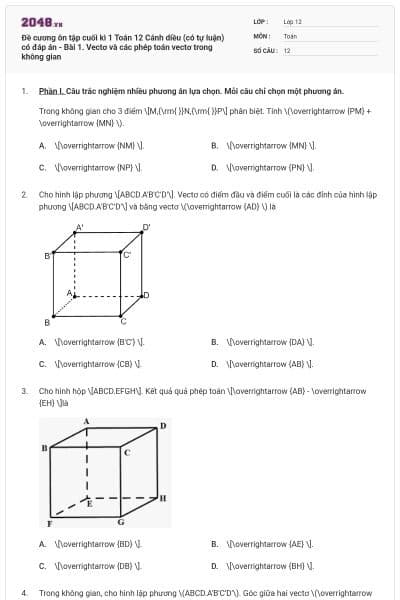
Cho hình lập phương \[ABCD.A'B'C'D'\]. Vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương \[ABCD.A'B'C'D'\] và bằng vectơ \(\overrightarrow {AD} \) là
![Do \[ABCD.A'B'C'D'\] là hình l (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/11-1761391014.png)
\[\overrightarrow {B'C'} \].
\[\overrightarrow {DA} \].
\[\overrightarrow {CB} \].
\[\overrightarrow {AB} \].
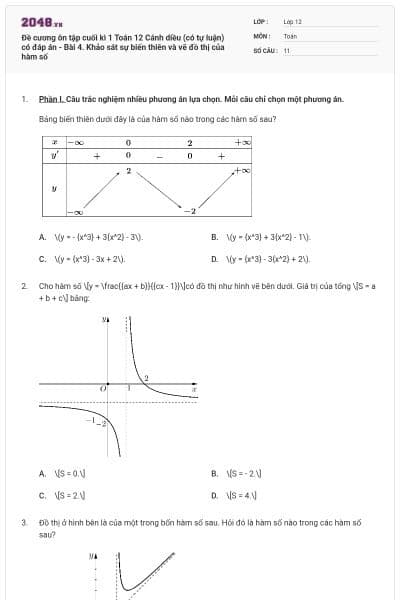
Cho hình hộp \[ABCD.EFGH\]. Kết quả quả phép toán \[\overrightarrow {AB} - \overrightarrow {EH} \]là
![Cho hình hộp \[ABCD.EFGH\]. Kết quả quả phép toán \[\overrightarrow {AB} - \overrightarrow {EH} \] là A. \[\overrightarrow {BD} \]. B. \[\overrightarrow {AE} \]. C. \[\overrightarrow {DB} \]. D. \[\overrightarrow {BH} \]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/12-1761391058.png)
\[\overrightarrow {BD} \].
\[\overrightarrow {AE} \].
\[\overrightarrow {DB} \].
\[\overrightarrow {BH} \].
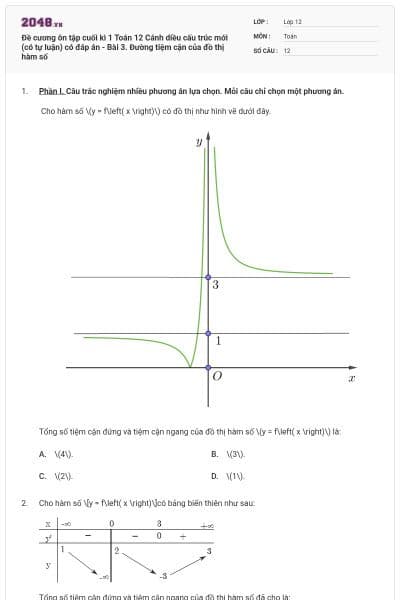
Trong không gian, cho hình lập phương \(ABCD.A'B'C'D'\). Góc giữa hai vectơ \(\overrightarrow {BD} \,,\,\overrightarrow {B'C} \)bằng
\(30^\circ \).
\(45^\circ \).
\(60^\circ \).
\(90^\circ \).
Cho \(\left| {\overrightarrow a } \right| = 2;\;\left| {\overrightarrow b } \right| = 6\), góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) bằng \(120^\circ \). Khẳng định nào dưới đây đúng?
\(\overrightarrow a .\overrightarrow b = 12\).
\[\overrightarrow a .\overrightarrow b = 40\].
\[\overrightarrow a .\overrightarrow b = - 6\].
\[\overrightarrow a .\overrightarrow b = 6\sqrt 3 \].
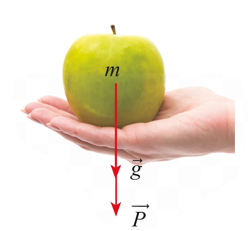
Nếu một vật có khối lượng \(m\;\left( {{\rm{kg}}} \right)\) thì lực hấp dẫn \(\vec P\) của Trái Đất tác dụng lên vật được xác định theo công thức \(\vec P = m\vec g\), trong đó \(\vec g\) là gia tốc rơi tự do có độ lớn \(g = 9,8\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}\). Tính độ lớn của lực hấp dẫn của Trái Đất tác dụng lên một quả táo có khối lượng 102 gam (Hình).
\(0,9996{\rm{N}}\).
\(0,5996{\rm{N}}\).
\(0,9196{\rm{N}}\).
\(0,8996{\rm{N}}\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông, \(SA\)vuông góc với mặt phẳng \((ABCD)\). Gọi \[I,J\] lần lượt là trung điểm của \[SA,SC\]. \[G\]là trọng tâm tam giác \[SBD\].
![Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là h (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/15-1761392134.png)
a) \(\overrightarrow {AC} - \overrightarrow {AB} = \overrightarrow {AD} \).
b) \(\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AG} \).
c) \[\overrightarrow {{\rm{IJ}}} .\overrightarrow {BD} = \overrightarrow 0 \].
d) \({\overrightarrow {AG} ^2} = {\overrightarrow {AS} ^2} + {\overrightarrow {AB} ^2} + {\overrightarrow {AD} ^2}\).
Cho hình lập phương \[ABCD.A'B'C'D'\], có cạnh \(a\).
a)\[\overrightarrow {AD'} .\overrightarrow {CC'} = {a^2}\].
b) \[\overrightarrow {AD'} .\overrightarrow {AB'} = {a^2}\].
c)\[\overrightarrow {AB'} .\overrightarrow {CD'} = 0\].
d) \[\left| {\overrightarrow {AC'} } \right| = a\sqrt 3 \].
Một vật nặng O được kéo từ ba hướng như hình vẽ và chịu tác dụng của 3 lực \[\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \] có độ lớn lần lượt là \(24N,12N,6N\). Biết góc tạo bởi 2 lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) là 120° và lực thứ ba vuông góc với hai lực đầu tiên.
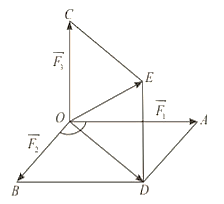
a)\(\overrightarrow {BO} + \overrightarrow {BA} = \overrightarrow {BD} \).
b) \(\overrightarrow {OE} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} \).
c) Độ dài của vectơ \(\overrightarrow {OD} \) là \(\left| {\overrightarrow {OD} } \right| = 12\sqrt 7 \).
d) Độ lớn hợp lực tác dụng vào vật \(O\) là \(6\sqrt {13} \) N.
Phần III. Trắc nghiệm trả lời ngắn
Cho tứ diện \(ABCD\). Gọi \(E\) là trung điểm \(AD\), \(F\) là trung điểm \(BC\). Khi đó \[\overrightarrow {AB} + \overrightarrow {DC} = k\overrightarrow {EF} \]. Tìm \(k\).
Chohình lập phương \(ABCD.A'B'C'D'\). Góc giữa hai véctơ \(\overrightarrow {A'B} \) và \(\overrightarrow {AC'} \) bằng bao nhiêu độ?
Cho tứ diện đều \(ABCD\) có độ dài cạnh bằng 1, gọi \(M\) là trung điểm cạnh \(CD\). Tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AM} \) bằng bao nhiêu?