Đề cương ôn tập cuối kì 1 Toán 12 Cánh diều (có tự luận) có đáp án - Bài 2. Tọa độ của vectơ

Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.

Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' biết rằng các điểm có toạ độ \[A\left( {2;1;0} \right),C\left( {0;3;0} \right),C'\left( { - 1;2;1} \right),D'\left( {0; - 2;0} \right)\].

a) Tọa độ các điểm \[A',B'\]là \[A'\left( {1;0; - 1} \right),B'\left( {0;4;2} \right)\].

b) Tọa độ các điểm \[B,D\]là \[B\left( {1;5;1} \right),D\left( {1; - 1; - 1} \right)\].

c) Tọa độ vectơ \[\overrightarrow {AB} \]là\[\overrightarrow {AB} = \overrightarrow i + 4\overrightarrow j + \overrightarrow k \].

d) Tọa độ vectơ \[\overrightarrow {B'D} \]là\[\overrightarrow {B'D} = \overrightarrow i - 5\overrightarrow j - 3\overrightarrow k \].

Trong không gian Oxyz, cho \(\vec a = \left( {2;2;0} \right),\vec b = \)\(2\vec j + 2\vec k\). Dựng \(\overrightarrow {OA} = \vec a\) và\(\overrightarrow {OB} = \vec b\).

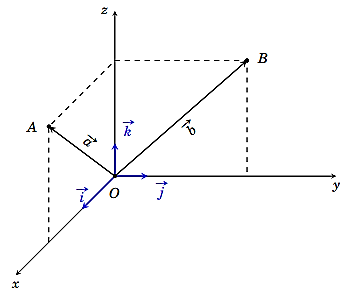
a) \(\vec a = 2\vec i + 2\vec k\).                             

b) Toạ độ \(\vec b = \left( {0;2;2} \right)\).

c) Toạ độ \(\overrightarrow {AB} = \left( { - 2;2;0} \right)\).                                                                                

d) Góc \(\widehat {AOB} = 45^\circ \).

Trong không gian Oxyz, cho các điểm \(A\left( {1;0;3} \right),B\left( {2;3; - 4} \right),C\left( { - 3;1;2} \right)\).

a) Điểm \(A\) thuộc mặt phẳng \(\left( {Oxz} \right)\).

b) \(\overrightarrow {BC} = 5\overrightarrow i + 2\overrightarrow j - 6\overrightarrow k \).

c) Điểm \(D\) thỏa mãn \(\overrightarrow {AB} = \overrightarrow {CD} \) là \(D\left( { - 2;4; - 5} \right)\).

d) Điểm \(P\) thỏa mãn \(PABC\) là hình bình hành là \(P\left( { - 4; - 2; - 9} \right)\).

Phần III. Trắc nghiệm trả lời ngắn

Trong không gian Oxyz, cho mặt phẳng hình hộp OABC.O'A'B'C' có \(A\left( {2\,;\,1\,;\, - 1} \right)\), \(B\left( {0\,;\,3\,;1} \right)\) và \(C'\left( {2\,;\, - 3\,;\,5} \right)\). Toạ độ điểm\(O'\left( {a;b;c} \right)\). Tính \(a + b + c\).

Trong không gian với một hệ trục toạ độ cho trước (đơn vị đo lấy theo km), ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm \(A\left( {800;500;7} \right)\) đến điểm \(B\left( {940;550;8} \right)\) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy bay sau 10 phút tiếp theo \(D\left( {x;y;z} \right)\). Tính \(x + y + z\).

Trong không gian Oxyz, cho điểm \(A\left( {10;7;24} \right)\). Gọi \(M\left( {a;b;c} \right)\) là điểm trên mặt phẳng \(\left( {Oyz} \right)\). Khi độ dài đoạn \(AM\) ngắn nhất, tính giá trị biểu thức \(T = a - 2b + c\).