Đề cương ôn tập cuối kì 1 Toán 12 Cánh diều (có tự luận) có đáp án - Bài 2. Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm
12 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Tuổi các học viên của một lớp tiếng Anh buổi tối ở một trung tâm ghi lại trong bảng tần số ghép lớp sau
Lớp | Tần số |
[15;20) | 10 |
[20;25) | 12 |
[25;30) | 14 |
[30;35) | 9 |
[35;40) | 5 |
Tính số trung bình.
26,2.
27,3.
28,4.
29,5.
Bảng dưới đây thống kê số giờ tự học ở nhà của 21 học sinh lớp 12 được hỏi ngẫu nhiên tại một trường THPT của Thành phố Hà Nội.
Nhóm(Số giờ tự học) | Tần số |
[0;2) | 6 |
[2;4) | 3 |
[4;6) | 7 |
[6;8) | 5 |
| 21 |
Khi đó phương sai của mẫu số liệu ghép nhóm trên là
\(5,19\).
\(5,29\).
\(5,91\).
\(2,28\).
Đo chiều cao (tính bằng\[{\rm{cm}}\]) của \[500\] học sinh trong một trường THPT ta thu được kết quả như sau:
![Đo chiều cao (tính bằng \[{\rm{cm}}\]) của \[500\] học sinh trong một trường THPT ta thu được kết quả như sau: Độ lệch chuẩn của mẫu số liệu trên là: A. \(s = 161,4\). B. \(s = 14,48\). C. \(s = 8,2\). D. \(s = 3,85\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/10-1761395174.png)
Độ lệch chuẩn của mẫu số liệu trên là:
\(s = 161,4\).
\(s = 14,48\).
\(s = 8,2\).
\(s = 3,85\)
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Bảng sau biểu diễn mẫu số liệu về số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua trà sữa ở một cửa hàng trong một buổi sáng.
Nhóm | \(\left[ {30;40} \right)\) | \(\left[ {40;50} \right)\) | \(\left[ {50;60} \right)\) | \(\left[ {60;70} \right)\) | \(\left[ {70;80} \right)\) |
Số khách hàng | 5 | 8 | 25 | 20 | 2 |
a) Số trung bình cộng của mẫu số liệu trên là 56 (nghìn đồng).
b) Khoảng biến thiên của mẫu số liệu trên là 50 (nghìn đồng).
c) Khoảng tứ phân vị của mẫu số liệu trên là 12,7 (nghìn đồng).
d) Phương sai của mẫu số liệu trên lớn hơn 93 (nghìn đồng).
Khối lượng của 30 củ khoai tây được thu hoạch ở một nông trại được thống kê như bảng sau:
Lớp khối lượng (gam) | Giá trị đại diện | Tần số |
\[\left[ {70;80} \right)\] | \[75\] | \[3\] |
\[\left[ {80;90} \right)\] | \[85\] | \[6\] |
\[\left[ {90;100} \right)\] | \[95\] | \[12\] |
\[\left[ {100;110} \right)\] | \[105\] | \[6\] |
\[\left[ {110;120} \right)\] | \[115\] | \[3\] |
|
| \[n = 30\] |
a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là \[50\].
b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là \[10\].
c) Số trung bình cộng của mẫu số liệu ghép nhóm trên là \[90\].
d) Phương sai của mẫu số liệu ghép nhóm trên là \[120\].
Số xe ô tô đi qua một trạm thu phí mỗi phút trong khoảng thời gian từ 10 giờ đến 10 giờ 20 phút sáng được thống kê như bảng sau:
Số xe | Giá trị đại diện | Tần số |
\[\left[ {6;10} \right)\] | \[8\] | \[5\] |
\[\left[ {10;14} \right)\] | \[12\] | \[9\] |
\[\left[ {14;18} \right)\] | \[16\] | \[3\] |
\[\left[ {18;22} \right)\] | \[20\] | \[9\] |
\[\left[ {22;26} \right)\] | \[24\] | \[4\] |
|
| \[n = 30\] |
a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là \[20\].
b) Số trung bình cộng của mẫu số liệu ghép nhóm trên là \[15,73\].
c) Phương sai của mẫu số liệu ghép nhóm trên là \[25,73\].
d) Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là \[4,36\].
Phần III. Trắc nghiệm trả lời ngắn
Kết quả khảo sát thời gian sử dụng liên tục (đơn vị: giờ) từ lúc sạc đầy cho đến khi hết của pin một số máy vi tính cùng loại được mô tả bằng biểu đồ bên.
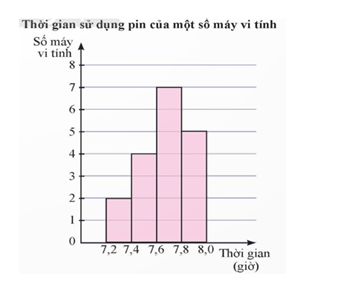
Xác định phương sai của thời gian sử dụng pin (làm tròn đến hàng phần trăm).
Các bạn học sinh lớp 12A trả lời 40 câu hỏi trong một bài kiểm tra. Kết quả được thống kê ở bảng sau:

Tính giá trị trung bình số câu trả lời đúng.
Sau khi điều tra về cân nặng của 40 học sinh trong lớp 12A ở một trường THPT X thu được kết quả trong mẫu ghép nhóm sau:
Nhóm | Tần số |
\[\left[ {30;40} \right)\] | \[2\] |
\[\left[ {40;50} \right)\] | \[10\] |
\[\left[ {50;60} \right)\] | \[16\] |
\[\left[ {60;70} \right)\] | \[8\] |
\[\left[ {70;80} \right)\] | \[2\] |
\[\left[ {80;90} \right)\] | \[2\] |
| \[n = 40\] |
Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên ( làm tròn kết quả đến hàng phần chục).
B. TỰ LUẬN
Tìm các khoảng đơn điệu và cực trị của các hàm số sau:
a) \(f(x) = - {x^3} + 3{x^2}\); b)\(g(x) = x + \frac{1}{x}\); c) \(h(x) = {x^3}\).
Tìm tất cả các giá thực của tham số \(m\) sao cho hàm số \(y = 2{x^3} - 3{x^2} - 6mx + m\) nghịch biến trên khoảng \(\left( { - 1;\,1} \right)\).
Với giá trị nào của tham số \(m\) để đồ thị hàm số \(y = {x^3} - 3{x^2} + m\) có hai điểm cực trị \(A\), \(B\) thỏa mãn \(OA = OB\) (\(O\) là gốc tọa độ)?