Đề cương ôn tập cuối kì 1 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
12 câu hỏi
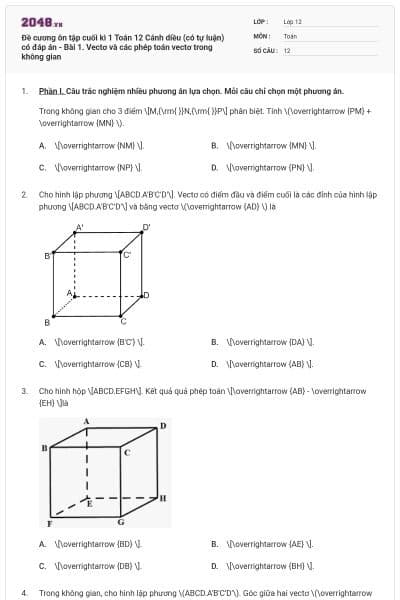
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
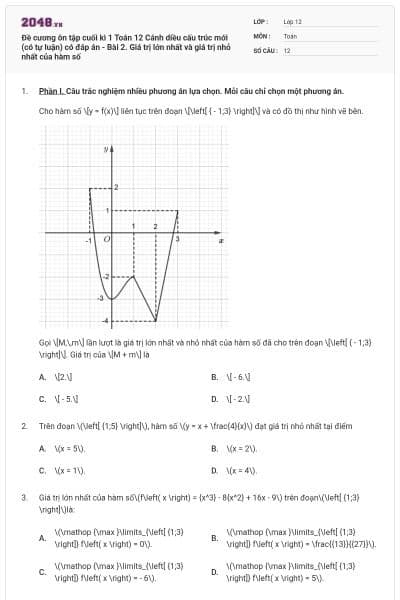
Cho hàm số \[y = f(x)\] liên tục trên đoạn \[\left[ { - 1;3} \right]\] và có đồ thị như hình vẽ bên.
![Từ đồ thị ta có: \[\left\{ \begin{array}{l}m = \mathop {\min }\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( { - 2} \right) = - 4\\M = \mathop {\max }\limits_{\left[ { - 1 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/10-1761388534.png)
Gọi \[M,\,m\] lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \[\left[ { - 1;3} \right]\]. Giá trị của \[M + m\] là
\[2.\]
\[ - 6.\]
\[ - 5.\]
\[ - 2.\]
Trên đoạn \(\left[ {1;5} \right]\), hàm số \(y = x + \frac{4}{x}\) đạt giá trị nhỏ nhất tại điểm
\(x = 5\).
\(x = 2\).
\(x = 1\).
\(x = 4\).
Giá trị lớn nhất của hàm số\(f\left( x \right) = {x^3} - 8{x^2} + 16x - 9\) trên đoạn\(\left[ {1;3} \right]\)là:
\(\mathop {\max }\limits_{\left[ {1;3} \right]} f\left( x \right) = 0\).
\(\mathop {\max }\limits_{\left[ {1;3} \right]} f\left( x \right) = \frac{{13}}{{27}}\).
\(\mathop {\max }\limits_{\left[ {1;3} \right]} f\left( x \right) = - 6\).
\(\mathop {\max }\limits_{\left[ {1;3} \right]} f\left( x \right) = 5\).
Tìm giá trị nhỏ nhất của hàm số \(f\left( x \right) = \left( {x - 3} \right){e^{2x}}\).
\[\mathop {\min }\limits_\mathbb{R} f\left( x \right) = - \frac{{{e^5}}}{2}\].
\[\mathop {\min }\limits_\mathbb{R} f\left( x \right) = \frac{{{e^5}}}{2}\].
\[\mathop {\min }\limits_\mathbb{R} f\left( x \right) = {e^5}\].
Không tồn tại.
Một vật chuyển động theo quy luật \[s = \frac{1}{3}{t^3} - {t^2} + 9t\], vớit (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường đi được trong thời gian đó. Hỏi trong khoảng thời gian 10 giây kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
\[89\left( {{\rm{m/s}}} \right).\]
\[71\left( {{\rm{m/s}}} \right).\]
\[109\left( {{\rm{m/s}}} \right).\]
\[\frac{{25}}{3}\left( {{\rm{m/s}}} \right)\].
Đồ thị bên dưới là tốc độ của một chiếc xe đua trên đoạn đường đua bằng phẳng dài 3 km.
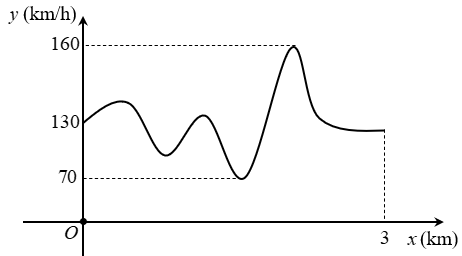
Tốc độ nhỏ nhất của xe đua trên đoạn đường này bằng
\(3\,\)(km/h).
\(160\,\)(km/h).
\(130\,\)(km/h).
\(70\,\)(km/h).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hàm số \(y = f\left( x \right) = {\log _2}\left( {{x^2} - 3x + 2} \right)\). a) Hàm số có giá trị lớn nhất trên khoảng \(\left( {2; + \infty } \right)\).
b) Hàm số luôn có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn \(\left[ { - 1;0} \right]\).
c) Trên đoạn \(\left[ { - 1;0} \right]\) hàm số có giá trị nhỏ nhất bằng 1.
d) Gọi \({m_0}\) là giá trị của tham số \(m\) để hàm số \(g\left( x \right) = {2^{f\left( x \right)}} + m\) có giá trị nhỏ nhất trên đoạn \(\left[ {3;4} \right]\) bằng \( - 3\). Khi đó \({m_0} \in \left( { - 5;0} \right)\).
Cho hàm số\(y = \sqrt {5 - 4x} \) trên đoạn\(\left[ { - 1;1} \right]\).
a)Giá trị lớn nhất và giá trị nhỏ nhất của hàm số là \(\mathop {\max }\limits_{\left[ { - 1;1} \right]} y = \sqrt 5 \)và \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} y = 0\).
b)Giá trị lớn nhất và giá trị nhỏ nhất của hàm số là\(\mathop {\max }\limits_{\left[ { - 1;1} \right]} y = 1\)và \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} y = - 3\).
c) Giá trị lớn nhất và giá trị nhỏ nhất của hàm số là\(\mathop {\max }\limits_{\left[ { - 1;1} \right]} y = 3\)và \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} y = 1\).
d)Giá trị lớn nhất và giá trị nhỏ nhất của hàm số là\(\mathop {\max }\limits_{\left[ { - 1;1} \right]} y = 0\)và \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} y = - \sqrt 5 \).
Cho hàm số \(y = f(x)\) xác định và liên tục trên \(\mathbb{R}\), có đồ thị như hình vẽ bên: 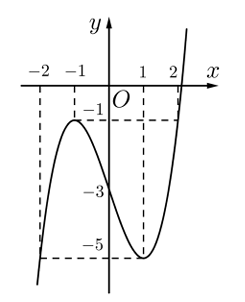
a) Giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 2;2} \right]\) là \( - 1\).
b) Giá trị nhỏ nhất của hàm số trên \(\left[ {0; + \infty } \right)\) là \( - 5\).
c) Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên \(\left( { - \infty ;1} \right]\) là 2.
d) Hàm số đạt giá trị nhỏ nhất trên đoạn \(\left[ { - 1;2} \right]\) tại điểm \(x = 1\).
Phần III. Trắc nghiệm trả lời ngắn
Tìm giá trị nhỏ nhất của hàm số \(f(x) = \frac{{{x^2} + 9}}{x}\) trên khoảng \((0; + \infty )\).
Một ông nông dân có \(240\)m hàng rào và muốn rào lại cánh đồng hình chữ nhật tiếp giáp với một con sông. Ông không cần rào cho phía giáp bờ sông. Hỏi ông có thể rào được cánh đồng với diện tích lớn nhất là bao nhiêu?
Một chất điểm chuyển động theo phương trình \(s\left( t \right) = - {t^3} + 6{t^2} + t + 3\), trong đó \(t\) tính bằng giây kể từ lúc chất điểm bắt đầu chuyển động và \(s\) tính bằng mét. Tính quãng đường chất điểm đi được kể từ lúc bắt đầu chuyển động đến khi chất điểm có vận tốc tức thời lớn nhất.