25 câu hỏi
Cho hàm số y = 2\(\sqrt x - x\)với x > 0. Tính y'(1) có kết quả là
3
2
0
1
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA ^ (ABC). Chọn khẳng định đúng
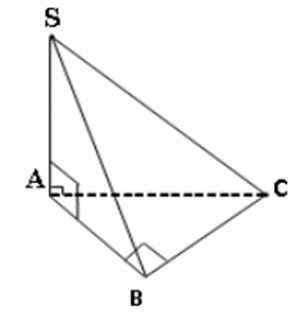
SA ^ SC
AB ^ AC
AB ^ SB
SA ^ BC
Mệnh đề nào sau đây đúng?
lim n = 0
lim \(\frac{{ - 1}}{n}\) = +¥
lim \(\frac{1}{{{n^3}}}\) = +¥
lim \({\left( {\frac{1}{4}} \right)^n}\)= 0
Tổng S = 1 + \(\frac{1}{2}\)+ \(\frac{1}{4}\)+ … + \(\frac{1}{{{2^n}}}\)+ … có giá trị là
S = \(\frac{3}{4}\)
S = \(\frac{3}{2}\)
S = 3
S = 2
Đạo hàm của hàm số y = 3sin2x + 2 là
y' = 6cos2x
y' = −6cos2x + 1
y' = 3cos2x – 2x
y' = 3cos2x + 2x
Mệnh đề nào sau đây sai?
\(\left( {\sqrt x } \right)' = \frac{1}{{\sqrt x }}(x > 0).\)
(c)' = 0 (c là hằng số).
(xn)' = n.xn – 1 (n Î ℕ, n > 1).
(x)' = 1.
bằng:
2.
\(\frac{5}{2}\).
+¥.
−¥.
Hàm số nào sau đây gián đoạn tại x0 = 1?
y = \(\frac{{{x^2} + 2x - 3}}{{x - 1}}\)
y = x2 – 1.
y = (x – 1)2
y = \(\frac{{x - 6}}{{x + 1}}\)
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính \(\overrightarrow {AB} .\overrightarrow {EG} \) bằng
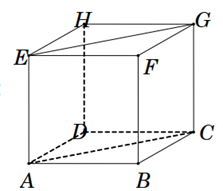
\({a^2}\frac{{\sqrt 2 }}{2}\)
a2
\({a^2}\sqrt 2 \)
\({a^2}\sqrt 3 \)
Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{3x + 1\,\,\,\,\,\,\,\,khi\,x \ne 1}\\{2x + 2a\,\,\,\,khi\,x = 1}\end{array}} \right.\). Giá trị của a để hàm số f(x) liên tục trên ℝ là
−2
1
−1
2
Cho hình chóp S.ABC có SA ^ (ABC).
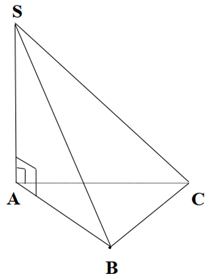
Góc giữa đường thẳng SC và mặt phẳng (ABC) là
SCB
SAC
SCA
CSA
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết rằng SA = SC, SB = SD. Khẳng định nào sau đây là đúng?
CD ^ AC
SO ^ (ABCD)
AB ^ (SAC)
CD ^ (SBD)
Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Đẳng thức đúng là
(uv)' = u'v + uv'
(uv)' = u'v'
(uv)' = u'v – uv'
(uv)' = uv
Cho hình hộp ABCD.A’B’C’D’. Khẳng định nào đúng?
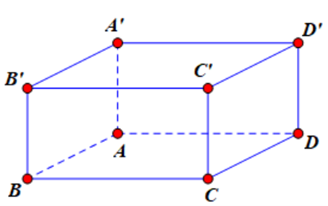
\(\overrightarrow {CB} + \overrightarrow {CD} + \overrightarrow {C'C} = \overrightarrow {CA'} \)
\(\overrightarrow {CB} + \overrightarrow {CD} + \overrightarrow {CC'} = \overrightarrow {CA'} \)
\(\overrightarrow {CB} + \overrightarrow {CD} + \overrightarrow {CC'} = \overrightarrow {CA} \)
\(\overrightarrow {CB} + \overrightarrow {CD} + \overrightarrow {CC'} = \overrightarrow {C'A'} \)
Cho hình lập phương ABCD.A’B’C’D’. Bộ ba vectơ nào sau đây đồng phẳng?
\(\overrightarrow {D'C'} ,\overrightarrow {D'D} ,\overrightarrow {AC} \)
\(\overrightarrow {B'C'} ,\overrightarrow {AD} ,\overrightarrow {A'B'} \)
\(\overrightarrow {CB} ,\overrightarrow {CD} ,\overrightarrow {CC'} \)
\(\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {AA'} \)
Trong các mệnh đề sau, mệnh đề nào sai?
\(\mathop {\lim }\limits_{x \to {0^ - }} \frac{1}{{{x^2}}} = - \infty \)
\(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{{x^3}}} = + \infty \)
\(\mathop {\lim }\limits_{x \to {0^ - }} \frac{1}{{{x^4}}} = + \infty \)
\(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{ - 1}}{{{x^4}}} = - \infty \)
Giới hạn \(\mathop {\lim }\limits_{x \to - 3} \frac{{{x^2} + 4x + 3}}{{x + 3}}\) có kết quả là:
−2
1
3
5
Cho hai hàm số f(x), g(x) thỏa mãn \(\mathop {\lim }\limits_{x \to 1} f(x)\)= −6 và \(\mathop {\lim }\limits_{x \to 1} g(x)\)= 3. Giá trị của \(\mathop {\lim }\limits_{x \to 1} \left[ {f(x) - g(x)} \right]\) bằng:
−3
−9
9
3
Hàm số nào sau đây liên tục trên ℝ?
y = \(\frac{{x + 1}}{{{x^2} + x - 2}}\)
y = \(\frac{{x - 1}}{{x + 1}}\)
y = x3 + cotx
y = x3 + 3x2
Giới hạn \(\mathop {\lim }\limits_{x \to - 2} ({x^2} + x + 1)\) có kết quả là giá trị nào sau đây?
5
7
1
3
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính d(AB,(EFGH)).
4a
2a
a
3a
Hàm số y = sinx có đạo hàm cấp hai là
y" = cosx
y" = sinx
y" = −cosx
y" = −sinx
Trong bốn giới hạn sau đây, giới hạn nào là −1?
un = \(\frac{{{n^2} + n}}{{ - 2n - {n^2}}}\)
un = \(\frac{{{n^3}}}{{{n^2} + 3}}\)
un = \(\frac{{2n + 3}}{{2 - 3n}}\)
un = \(\frac{{{n^2} - {n^3}}}{{2{n^3} + 1}}\)
Tính đạo hàm của hàm số y = \(\frac{{x + 1}}{{x - 2}}.\) Kết quả là
y' = \(\frac{3}{{{{(x - 2)}^2}}}\)
y' = \( - \frac{3}{{{{(x - 2)}^2}}}\)
y' = \( - \frac{1}{{{{(x - 2)}^2}}}\)
y' = \(\frac{1}{{{{(x - 2)}^2}}}\)
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \)và \(\overrightarrow {DH} \)?
60°
45°
90°
120°
