Bộ 5 đề thi học kì 1 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 3
21 câu hỏi
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Dãy số nào sau đây không phải là dãy các số hữu tỉ?
\( - 0,5;{\rm{ 3}}\frac{1}{5};{\rm{ }} - 2,75;{\rm{ 10}}{\rm{.}}\)
\(\frac{0}{3};{\rm{ }}\frac{{ - 1}}{6};{\rm{ 75\% ; }} - 10.\)
\(\sqrt 4 ;{\rm{ }}0;{\rm{ }}75\% ;{\rm{ }}5,12.\)
\( - 3\frac{1}{5};{\rm{ }}\frac{3}{4};{\rm{ }}\sqrt 3 ;{\rm{ }} - 10.\)
Kết quả của phép tính \(0,{6^5}:0,{6^3}\) là
\(0,{6^8}.\)
\(0,{6^2}.\)
\(0,{6^{15}}.\)
\(0,{6^3}.\)
Phân số nào dưới đây viết được dưới dạng số thập phân vô hạn tuần hoàn?
\(\frac{{15}}{{42}}.\)
\(\frac{{19}}{4}.\)
\(\frac{5}{8}.\)
\(\frac{8}{{25}}.\)
Một số dương \(a\) có căn bậc hai số học là
\(\sqrt a .\)
\( - \sqrt a .\)
\(\sqrt a \) và \( - \sqrt a .\)
\({a^2}.\)
Giá trị tuyệt đối của \( - 3,14\) là
\(3,14.\)
\( - 3,14.\)
\(0.\)
\({\left( { - 3,14} \right)^2}.\)
Với hai số thực \(a,b\) thỏa mãn \(2025a = 2024b,{\rm{ }}\left( {a,b \ne 0} \right)\). Khẳng định sai là
\(\frac{a}{b} = \frac{{2024}}{{2025}}.\)
\(\frac{{2024}}{a} = \frac{{2025}}{b}.\)
\(\frac{a}{{2025}} = \frac{b}{{2024}}.\)
\(\frac{b}{{2025}} = \frac{a}{{2024}}.\)
Biết hai đại lượng \(x\) và \(y\) tỉ lệ thuận với nhau khi \(x = 4\) thì \(y = 8,\) khi đó hệ số tỉ lệ \(k\) của \(y\) đối với \(x\) là
\(8.\)
\(32.\)
\(0,5.\)
\(2.\)
Biết hai đại lượng \(x\) và \(y\) tỉ lệ nghịch theo hệ số tỉ lệ là \(a\). Nếu \(x = - 3\) thì \(y = - 12\). Vậy hệ số tỉ lệ \(a\) là
\(4.\)
\( - 4.\)
\(36.\)
\( - 36.\)
Cho các kích thước của hình hộp chữ nhật \(ABCD.EFGH\) như sau: \(HG = 38{\rm{ cm; }}BF = 26{\rm{ cm}}{\rm{.}}\)
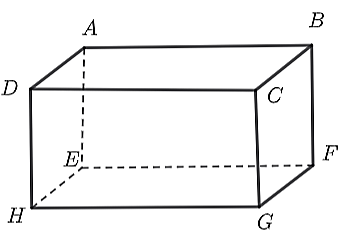
Hỏi độ dài của \(AB\) và \(CG\) là bao nhiêu cm?
\(AB = 26{\rm{ cm; }}CG = 38{\rm{ cm}}{\rm{.}}\)
\(AB = 28{\rm{ cm; }}CG = 64{\rm{ cm}}{\rm{.}}\)
\(AB = 12{\rm{ cm; }}CG = 38{\rm{ cm}}{\rm{.}}\)
\(AB = 38{\rm{ cm; }}CG = 26{\rm{ cm}}{\rm{.}}\)
Hình hộp chữ nhật, hình lập phương, hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác có chung đặc điểm nào dưới đây?
Đều có 6 măt.
Đều có 8 đỉnh.
Các mặt đáy song song với nhau.
Mỗi đỉnh có 3 góc vuông.
Cho tia \(Ot\) là tia phân giác của \(\widehat {xOy}\). Nếu \(\widehat {xOt} = 35^\circ \) thì \(\widehat {yOt}\) bằng
\(35^\circ .\)
\(90^\circ .\)
\(180^\circ .\)
\(70^\circ .\)
Cho ba đường thẳng phân biệt \(a,b,c.\) Khẳng định nào sau đây là đúng?
Nếu \(a\parallel b;{\rm{ }}b\parallel c\) thì \(a \bot c.\)
Nếu \(a \bot b;{\rm{ }}b \bot c\) thì \(a \bot c.\)
Nếu \(a \bot b;{\rm{ }}b\parallel c\) thì \(a\parallel c.\)
Nếu \(a\parallel b;{\rm{ }}b\parallel c\) thì \(a\parallel c.\)
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Một cửa hàng nhập về 100 cái áo với giá gốc \(200{\rm{ }}000\) đồng/cái. Cửa hàng đã bán 60 cái áo với giá mỗi cái lãi \(25\% \) so với giá gốc; 40 cái còn lại bán lỗ \(5\% \) so với giá gốc.
a) Khi bán 60 cái đầu, mỗi cái áo lãi \(50{\rm{ }}000\) đồng.
b) Khi bán 40 cái còn lại, mỗi cái lỗ \(10{\rm{ }}000\) đồng.
c) Số tiền thu về khi bán 100 cái áo nhỏ hơn \(22\) triệu đồng.
d) Cửa hàng đã lãi \(1,5\) triệu đồng.
Nhà ông An thuê thợ làm một cái gờ bằng bê tông để xe máy lên xuống bậc thêm có hình dạng giống như hình lăng trụ đứng tam giác dưới đây.
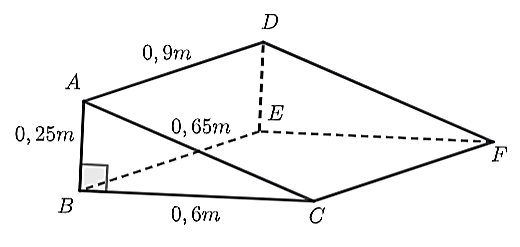
Biết rằng \(AB = 0,25{\rm{ m; }}BC = 0,6{\rm{ m; }}AC{\rm{ = 0,65 m; }}AD = 0,9{\rm{ m}}\). Cho biết, tiền quét vôi các mặt xung quanh (trừ hai mặt đáy) của gờ là \(300{\rm{ 000}}\) đồng và tiền đổ bê tông là \(1{\rm{ d}}{{\rm{m}}^3}\) giá \(50{\rm{ 000}}\) đồng.
a) Diện tích được quét vôi của cái gờ là \(1,35\) m2.
b) Thể tích của gờ lớn hơn \(0,05{\rm{ }}{{\rm{m}}^3}.\)
c) Số tiền mua bê tông làm chiếc gờ này nhỏ hơn \(3,3\) triệu đồng.
d) Tổng số tiền ông An phải trả là \(3,5\) triệu đồng.
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Ta có \(a = \sqrt 3 = 1,7320508.....\) Hãy làm tròn số \(a\) đến chữ số thập phân thứ hai sau dấu phẩy.
Tìm \(x,\) biết: \(\frac{1}{4}x + \frac{5}{4} = \sqrt {\frac{9}{{16}}} \).
Cho một hình trụ đứng tam giác vuông \(ABC.A'B'C'\) có \(AB = 40{\rm{ cm,}}\) \(AC = 60{\rm{ cm,}}\) \(CC' = 50{\rm{ cm}}{\rm{.}}\) Hỏi thể tích của hình lăng trụ đứng tam giác này bằng bao nhiêu mét khối?
Trong hình vẽ có \(xy\parallel mn\). Tia \(BC\) là tia phân giác của \(\widehat {ABn}.\) Biết \(\widehat {BAx} = 70^\circ \).
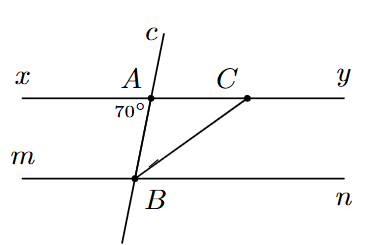
Hỏi số đo \(\widehat {ACB}\) bằng bao nhiêu độ?
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Ba đội máy cày, cày ba cánh đồng có cùng diện tích. Đội thứ nhất cày trong 5 ngày, đội thứ hai cày trong 4 ngày và đội thứ ba cày trong 6 ngày. Hỏi mỗi đội có bao nhiêu máy cày, biết rằng ba đội có tất cả \(37\) máy? (Năng suất các máy là như nhau).
(1,5 điểm) Cho hình vẽ bên , biết: \(\widehat {FDC} = 135^\circ ;\widehat {{\rm{ }}CBx} = 45^\circ ;\widehat {{\rm{ }}DCz} = 135^\circ ,{\rm{ }}Dy\parallel Bx,{\rm{ }}Dy \bot BF\) tại điểm \(F.\)
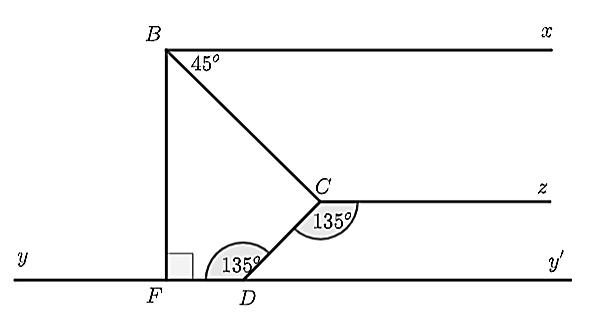
a) Chứng minh \(Cz\parallel Dy.\)
b) Chứng minh \(BC\) là tia phân giác của \(\widehat {FBx}.\)
c) Kẻ tia \(Ct\) là tia đối của tia \(Cz\). Chứng minh \(Ct\) là tia phân giác của \(\widehat {DCB}\).
(0,5 điểm) Cho \(S = \frac{1}{4} + \frac{2}{{{4^2}}} + \frac{3}{{{4^3}}} + \frac{4}{{{4^4}}} + .... + \frac{{2023}}{{{4^{2023}}}}\). Chứng minh \(S < \frac{1}{2}.\)








