Bộ 5 đề thi học kì 1 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 1
21 câu hỏi
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Số đối của số \(\frac{{ - 7}}{4}\) là
\(\frac{{ - 4}}{7}.\)
\(\frac{4}{7}.\)
\(\frac{7}{4}.\)
\(\frac{7}{{ - 4}}.\)
Kết quả của phép tính \({\left( {\frac{2}{3}} \right)^7}:{\left( {\frac{2}{3}} \right)^3}\) là
\({\left( {\frac{2}{3}} \right)^4}.\)
\({\left( {\frac{2}{3}} \right)^5}.\)
\({\left( {\frac{2}{3}} \right)^{10}}.\)
\({\left( {\frac{2}{3}} \right)^{21}}.\)
Số thập phân \( - 0,375\) được viết dưới dạng phân số tối giản là
\( - \frac{{375}}{{1000}}.\)
\( - \frac{3}{8}.\)
\( - \frac{{71}}{{200}}.\)
\( - \frac{{125}}{{1273}}.\)
Khẳng định nào sau đây là đúng?
\(\sqrt {0,04} = 0,16.\)
\(\sqrt {0,04} = - 0,16.\)
\(\sqrt {0,04} = - 0,2.\)
\(\sqrt {0,04} = 0,2.\)
Khẳng định đúng là
\(\left| { - 3,7} \right| = - 3,7.\)
\(\left| { - 3,7} \right| = 3,7.\)
\(\left| { - 3,7} \right| = \pm 3,7.\)
\(\left| { - 3,7} \right| > 3,7.\)
Chọn câu sai. Nếu \(a.d = b.c\) và \(a,b,c,d \ne 0\) thì
\(\frac{a}{c} = \frac{b}{d}.\)
\(\frac{a}{b} = \frac{c}{d}.\)
\(\frac{a}{b} = \frac{d}{c}.\)
\(\frac{d}{c} = \frac{b}{a}.\)
Nếu \(a,b,c\) tỉ lệ với các số \(2;3;5\) ta viết
\(\frac{a}{2} = \frac{b}{5} = \frac{c}{3}.\)
\(\frac{a}{2} = \frac{b}{3} = \frac{c}{5}.\)
\(\frac{a}{3} = \frac{b}{2} = \frac{c}{5}.\)
\(\frac{a}{5} = \frac{b}{3} = \frac{c}{2}.\)
Công thức nào sau đây cho biết \(y\) tỉ lệ nghịch với \(x\) theo hệ số tỉ lệ \(2025\)?
\(y = 2025x.\)
\(y = \frac{x}{{2025}}.\)
\(y = \frac{{2025}}{x}.\)
\(x = 2025y.\)
Các mặt bên của hình lăng trụ đứng tứ giác là
Các hình bình hành.
Các hình chữ nhật.
Các hình vuông.
Các hình thang cân.
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(BB' = 7{\rm{ cm}}{\rm{.}}\) Khẳng định nào sau đây là đúng?
\(A'D' = 7{\rm{ cm}}{\rm{.}}\)
\(CC' = 7{\rm{ cm}}{\rm{.}}\)
\(D'C' = 7{\rm{ cm}}{\rm{.}}\)
\(AC' = 7{\rm{ cm}}{\rm{.}}\)
Chứng minh định lí là
dùng hình vẽ để từ giả thiết suy ra kết luận.
dùng lập luận để từ giả thiết suy ra kết luận.
dùng hình vẽ và đo đạc thực tế để từ giả thiết suy ra kết luận.
dùng đo đạc thực tế để từ giả thiết suy ra kết luận.
Theo tiên đề Euclid được phát biểu: “Qua một điểm \(M\) nằm ngoài đường thẳng \(a\)….”
có duy nhất một đường thẳng đi qua \(M\) và song song với \(a.\)
có hai đường thẳng song song với \(a.\)
có ít nhất một đường thẳng song song với \(a.\)
có vô số đường thẳng song song với \(a.\)
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Bạn An đọc một cuốn sách trong 4 ngày. Ngày thứ nhất đọc được \(\frac{1}{6}\) quyển sách, ngày thứ hai đọc được \(\frac{1}{4}\) quyển sách, ngày thứ ba đọc được \(\frac{1}{5}\) quyển sách.
a) Trong ba ngày đầu, An đọc được \(\frac{{37}}{{60}}\) quyển sách.
b) Ngày thứ tư An đọc được ít hơn \(\frac{1}{3}\) phần quyển sách.
c) Ngày thứ tư An đọc được nhiều trang sách nhất.
d) Hai ngày đầu An đọc được nhiều hơn hai ngày sau.
Một xe container có thùng hàng dạng hình hộp chữ nhật, kích thước lòng trong thùng hàng dài \(5,8{\rm{ m,}}\) rộng \(3,2{\rm{ m,}}\) cao \(2{\rm{ m}}{\rm{.}}\) Người ta xếp vào thùng container những thùng hàng có dạng hình hộp chữ nhật có chiều dài \(50{\rm{ cm,}}\) chiều rộng \({\rm{40 cm,}}\) chiều cao\(20{\rm{ cm}}{\rm{.}}\) Biết rằng cứ 10 thùng hàng thì xe container nhận \(5{\rm{ 000}}\) đồng tiền công.
a) Thể tích của lòng thùng container là \(37,12{\rm{ }}{{\rm{m}}^3}.\)
b) Thể tích của các thùng hàng là \({\rm{0,4 }}{{\rm{m}}^3}.\)
c) Xe container đó chở được nhiều hơn \(900\) thùng hàng.
d) Xe nhận được \(4{\rm{ }}640{\rm{ }}000\) đồng tiền công.
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Khi làm tròn số \(a = 2,34682\) với độ chính xác \(0,005\) thì ta được kết quả bằng bao nhiêu?
Tìm giá trị của \(x,\) biết: \(\left( {\frac{1}{2} - x} \right) + \frac{3}{4} = \sqrt {\frac{{16}}{{25}}} \) (Kết quả ghi dưới dạng số thập phân).
Một hình hộp chữ nhật có đáy là hình vuông và thể tích là \(150{\rm{ c}}{{\rm{m}}^3}\). Chiều cao của hình hộp bằng \(6{\rm{ cm}}{\rm{.}}\) Hỏi chu vi đáy của hình hộp chữ nhật đó bằng bao nhiêu centimet?
Cho hình vẽ sau, biết \(a\parallel n\parallel b\).
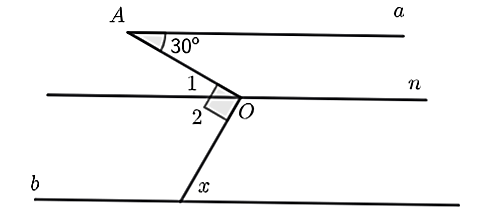
Hỏi số đo góc \(x\) bằng bao nhiêu độ?
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Trong đợt thi đua xây dựng Thư viện số của một trường THCS nhân dịp “Ngày chuyển đổi số quốc gia”, số quyển sách mà ba lớp 7A, 7B, 7C chuyển về dạng video ngắn lần lượt tỉ lệ thuận với \(13;17\) và \(22\). Biết tổng số quyển sách đã chuyển đối của hai lớp 7B và 7C nhiều hơn số quyển sách của lớp 7A là \(78\) quyển. Tính số quyển sách mỗi lớp đã chuyển về dạng video ngắn.
(1,5 điểm) Cho hình vẽ bên, biết \(Ay\) là phân giác của \(\widehat {xAC}.\)
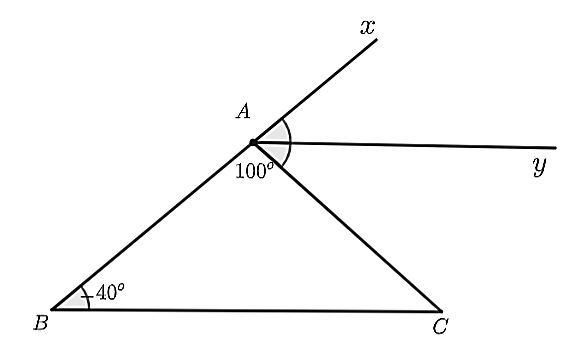
a) Vẽ lại hình (đúng số đo các góc ) và nêu giả thiết kết luận cho bài toán.
b) Chứng minh \(Ay\parallel BC\).
c) Kẻ tia \(Az\) nằm trong \(\widehat {BAC}\) sao cho \(\widehat {zAy} = 90^\circ \). Chứng minh tia \(Az\) là phân giác của \(\widehat {BAC}.\)
(0,5 điểm) Cho biểu thức \(A = - \frac{1}{3} + \frac{1}{{{3^2}}} - \frac{1}{{{3^3}}} + \frac{1}{{{3^4}}} - \frac{1}{{{3^5}}} + ... + \frac{1}{{{3^{100}}}}\). Tính giá trị của biểu thức \(B = 4\left| A \right| + \frac{1}{{{3^{100}}}}\).








