Bộ 5 đề thi giữa kì 2 Toán 6 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 4
21 câu hỏi
A. TRẮC NGHIỆM
Trong các cách viết sau đây, cách viết nào cho ta phân số?
\(\frac{4}{{ - 2,5}}.\)
\(\frac{{6,23}}{{1,68}}.\)
\(\frac{0}{{ - 2}}.\)
\(\frac{{ - 5}}{0}.\)
Hai phân số \(\frac{c}{d}\) và \(\frac{m}{n}\) (\(c,d,m,n\) là các số nguyên khác \(0\)) gọi là bằng nhau nếu
\(c.m = d.n.\)
\(c.n = d.m.\)
\(c.d = m.n.\)
\(c:n = d:m.\)
Phân số nào sau đây bằng phân số \(\frac{3}{2}\)?
\(\frac{{25}}{{20}}.\)
\(\frac{{24}}{{16}}.\)
\(\frac{{75}}{{10}}.\)
\(\frac{4}{6}.\)
Trong các phân số \(\frac{3}{9};\frac{4}{{ - 6}};\frac{2}{7};\frac{6}{{14}}\) phân số tối giản là
\(\frac{3}{9}.\)
\(\frac{4}{{ - 6}}.\)
\(\frac{2}{7}.\)
\(\frac{6}{{14}}.\)
Số đối của phân số \(\frac{{15}}{7}\) là
\( - \frac{{15}}{7}.\)
\(\frac{{15}}{7}.\)
\(\frac{7}{{15}}.\)
\(\frac{{ - 7}}{{15}}.\)
Hỗn số \(7\frac{3}{{11}}\) được viết dưới dạng phân số là
\(\frac{{77}}{{14}}.\)
\(\frac{{21}}{{11}}.\)
\(\frac{{10}}{{11}}.\)
\(\frac{{80}}{{11}}.\)
Chữ cái nào sau đây có trục đối xứng?
\({\rm{Q}}{\rm{.}}\)
\({\rm{P}}{\rm{.}}\)
\({\rm{E}}{\rm{.}}\)
\({\rm{N}}{\rm{.}}\)
Trong các câu sau, câu nào sai?
Hình lục giác là hình có sáu tâm đối xứng.
Hình tròn có một tâm đối xứng là tâm của đường tròn.
Hình bình hành có tâm đối xứng là giao điểm của hai đường chéo.
Hình thang cân không có tâm đối xứng.
Điểm \(M\) không thuộc đường thẳng \(d\) được kí hiệu là
\(M \in d.\)
\(M \notin d.\)
\(M \not\subset d.\)
\(d \in M.\)
Trong hình vẽ dưới đây, đường thẳng nào đi qua hai điểm \(M\) và \(N\).
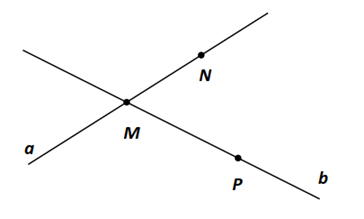
Đường thẳng \(b.\)
Đường thẳng \(MP.\)
Đường thẳng \(a.\)
Đường thẳng \(NP.\)
Đường thẳng \(a\) chứa những điểm nào?
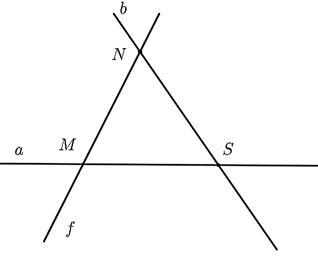
\(M,N.\)
\(M,S.\)
\(N,S.\)
\(M,N,S.\)
Chọn khẳng định sai trong các khẳng định sau.
Một điểm có thể thuộc đồng thời nhiều đường thẳng.
Với một đường thẳng \(a\) cho trước, có những điểm thuộc \(a\) và những điểm không thuộc \(a\).
Trên đường thẳng chỉ có duy nhất một điểm.
Một đường thẳng có thể đi qua nhiều điểm.
Hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d)
Lớp 6A của một trường THCS có \(40\) học sinh và được xếp loại: Giỏi, Khá, Trung bình. Biết số học sinh khá bằng \(\frac{3}{5}\) số học sinh cả lớp, số học sinh giỏi bằng \(\frac{3}{4}\) số học sinh còn lại.
a) Số học sinh Giỏi và Trung bình chiếm \(\frac{2}{5}\) số học sinh cả lớp.
b) Lớp 6A có \(24\) học sinh khá.
c) Số học sinh giỏi và trung bình của lớp 6A là \(12\) học sinh.
d) Lớp 6A có \(4\) học sinh trung bình.
Hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Cho hình vẽ sau.
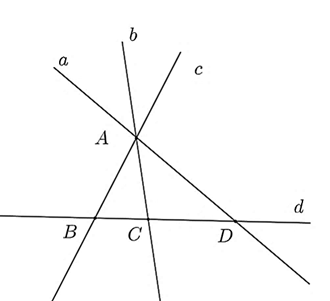
a) Điểm \(A\) thuộc các đường thẳng \(a,b,c\).
b) Điểm \(A\) không thuộc đường thẳng \(d\).
c) Có duy nhất một bộ ba điểm thẳng hàng trong hình vẽ trên.
d) Trên đường thẳng \(d\) lấy thêm bốn điểm phân biệt \(M,N,P,Q\) không trùng với điểm \(B,C,D.\). Khi đó, có tất cả \(8\) đường thẳng đi qua điểm \(A\) và một trong các điểm \(M,N,P,Q,B,C,D.\)
Hãyviết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Tìm giá trị của \(x,\) biết: \(\frac{{ - 4}}{5} = \frac{{16}}{x}.\)
Trả lời:
Hãyviết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Tìm giá trị của \(x,\) biết: \(x + \frac{3}{{10}} = \frac{{ - 7}}{{25}}:\frac{2}{5}\).
Trả lời:
Hãyviết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Một người đi xe đạp được \(5\frac{1}{4}{\rm{ km}}\) trong giờ đầu tiên. Giờ thứ hai đạp được \(\frac{{19}}{4}{\rm{ km}}{\rm{.}}\) Hỏi người đó phải đi quãng đường dài bao nhiêu kilomet nữa để đi hết đoạn đường, biết cả đoạn đường dài \(12{\rm{ km}}\).
Trả lời:
Hãyviết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Cho \(n\) đường, trong đó bất cứ hai đường thẳng nào cũng cắt nhau, không có ba đường thẳng nào cùng đi qua một điểm. Biết số giao điểm tạo thành là \(406\) giao điểm. Tính số đường thẳng.
Trả lời:
B. TỰ LUẬN
Thực hiện các phép tính sau (Tính hợp lí nếu có thể)
a) \(5\frac{3}{7} + \left( {1\frac{8}{{15}} - 4\frac{3}{7}} \right) - 4\frac{7}{{15}}.\)
b) \(\frac{1}{6} + \frac{1}{{12}} + \frac{1}{{20}} + \frac{1}{{30}} + \frac{1}{{42}}\).
2.1. Hãy vẽ tất cả các trục đối xứng của hình sau:
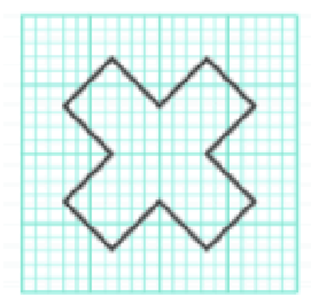
2.2. a) Vẽ ba điểm \(H,I,K\) không thẳng hàng, sau đó nối \(H\) với \(I\), nối \(I\) với \(K\), nối \(H\) với \(K\). Vẽ đường thẳng \(a\) cắt \(HI\) tại \(A\) (điểm \(A\) không trùng với \(H\) và \(I\)) và cắt đường thẳng \(HK\) tại \(B\) sao cho điểm \(K\) nằm giữa \(H\) và \(B\).
b) Từ hình vẽ câu a), hãy biểu diễn bằng kí hiệu các điểm thuộc và không thuộc đường thẳng \(a\).
Chứng tỏ rằng \(\frac{1}{{11}} + \frac{1}{{12}} + \frac{1}{{13}} + ... + \frac{1}{{70}} < \frac{5}{2}.\)








