Bộ 5 đề thi giữa kì 2 Toán 10 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Đề 3
20 câu hỏi
Biểu thức nào sau đây không là hàm số theo biến \(x\)?
\(y = \sqrt {{x^2} - 1} \).
\({y^4} = {x^3}\).
\(y = 5{x^2} - 3x + 4\).
\(y = x\).
Cho \(f\left( x \right) = a{x^2} + bx + c,\left( {a \ne 0} \right)\) có \(\Delta = {b^2} - 4ac < 0\). Khẳng định nào sau đây là đúng?
\(f\left( x \right)\) không đổi dấu trên \(\mathbb{R}\).
\(f\left( x \right) > 0,\forall x \in \mathbb{R}\).
Tồn tại \(x\) để \(f\left( x \right) = 0\).
\(f\left( x \right) < 0,\forall x \in \mathbb{R}\).
Giá trị \(x = 2\) là nghiệm của phương trình nào sau đây?
\(x + 2 = \sqrt {x - 1} \).
\(x - 1 = \sqrt {x - 3} \).
\(x + 2 = 2\sqrt {3x - 2} \).
\(\sqrt {{x^2} - x - 4} = \sqrt {x - 4} \).
Cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 3 - 5t\\y = 1 + 4t\end{array} \right.\). Một vectơ chỉ phương của \(\Delta \) là:
\(\overrightarrow {{u_1}} = \left( {3;1} \right)\).
\(\overrightarrow {{u_2}} = \left( { - 5;4} \right)\).
\(\overrightarrow {{u_3}} = \left( {4;5} \right)\).
\(\overrightarrow {{u_4}} = \left( {1;3} \right)\).
Góc \(\varphi \) giữa hai đường thẳng \({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) và \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) được xác định theo công thức
\(\cos \varphi = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} + \sqrt {a_1^2 + b_1^2} }}\).
\(\cos \varphi = \sqrt {\frac{{{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}}}{{{a^2} + {b^2}}}} \).
\(\cos \varphi = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} \sqrt {a_2^2 + b_2^2} }}\).
\(\cos \varphi = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {a_1^2 + b_1^2} \sqrt {a_2^2 + b_2^2} }}\).
Cho elip \(\left( E \right)\) có phương trình chính tắc \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\). Tổng khoảng cách từ một điểm \(M\) bất kì trên \(\left( E \right)\) đến hai tiêu điểm là
\(6\).
\(4\).
\(3\).
\(9\).
Cho hàm số \(y = a{x^2} + bx + c\) có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng?
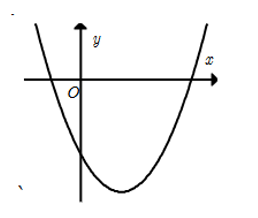
\(a > 0,b < 0,c < 0\).
\(a > 0,b < 0,c > 0\).
\(a > 0,b > 0,c > 0\).
\(a < 0,b < 0,c < 0\).
Tập nghiệm của bất phương trình \( - {x^2} + 5x + 6 > 0\) là
\(\left( { - 1;6} \right)\).
\(\left\{ { - 1;6} \right\}\).
\(\left[ { - 1;6} \right]\).
\(\left( { - \infty ; - 1} \right) \cup \left( {6; + \infty } \right)\).
Tổng tất cả các nghiệm của phương trình \(\sqrt {{x^2} + 2x - 3} = \sqrt {15 - 5x} \) là
\(7\).
\( - 7\).
\(6\).
\(4\).
Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \[\Delta :\left\{ \begin{array}{l}x = 2 + 3t\\y = - 1 + t\end{array} \right.\left( {t \in \mathbb{R}} \right)\] và điểm \(M\left( { - 1;6} \right)\). Phương trình đường thẳng đi qua \(M\) và vuông góc với \(\Delta \) là:
\(x - 3y + 19 = 0\).
\(x + 3y - 17 = 0\).
\(3x - y + 9 = 0\).
\(3x + y - 3 = 0\).
Trong mặt phẳng tọa độ \(Oxy\), góc tạo bởi hai đường thẳng \({d_1}:2x - y - 10 = 0\) và \({d_2}:x - 3y + 9 = 0\) có số đo bằng
\(60^\circ \).
\(30^\circ \).
\(135^\circ \).
\(45^\circ \).
Trong mặt phẳng \(Oxy\), đường tròn \(\left( C \right)\) đi qua hai điểm \(A\left( {5; - 1} \right),B\left( { - 3;7} \right)\). Đường tròn có đường kính \(AB\) có phương trình là
\({x^2} + {y^2} - 2x - 6y - 22 = 0\).
\({x^2} + {y^2} - 2x - 6y + 22 = 0\).
\({x^2} + {y^2} - 2x - y + 1 = 0\).
\({x^2} + {y^2} + 6x + 5y + 1 = 0\).
Cho hàm số \(y = a{x^2} + bx + c\left( {a,b,c \in \mathbb{R}} \right)\) có đồ thị như hình vẽ bên
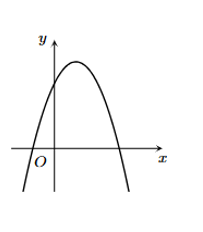
a) Hàm số đồng biến trên \(\left( { - \infty ;0} \right)\).
b) Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ dương.
c) \(c > 0\).
d)\(a < 0;b > 0\).
Trong mặt phẳng \(Oxy\), cho đường tròn \(\left( C \right)\) có phương trình \({x^2} + {y^2} - 6x + 2y + 6 = 0\) và hai điểm \(A\left( {1; - 1} \right),B\left( {1;3} \right)\).
a) Điểm \(A\) thuộc đường tròn.
b) Điểm \(B\) nằm trong đường tròn.
c)\(x = 1\) phương trình tiếp tuyến của \(\left( C \right)\) tại điểm \(A\).
d) Qua \(B\) kẻ được hai tiếp tuyến với \(\left( C \right)\) có phương trình lần lượt là \(x = 1\) và \(3x + 4y - 12 = 0\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên dưới. Giá trị của \(f\left( 2 \right)\)bằng bao nhiêu?
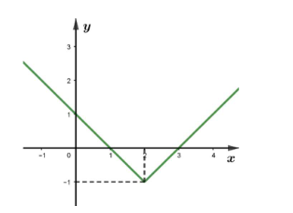
Trong mặt phẳng tọa độ \(Oxy\), cho parabol \(\left( P \right):{y^2} = 2px\left( {p > 0} \right)\). Biết khoảng cách từ tiêu điểm \(F\) đến đường thẳng \(\Delta :x + y - 12 = 0\) bằng \(2\sqrt 2 \). Tính tổng các giá trị của \(p\) thỏa mãn đề bài.
Một quả bóng được ném thẳng lên từ độ cao 1,6 m so với mặt đất với vận tốc 10 m/s. Độ cao của bóng so với mặt đất (tính bằng mét) sau t giây được cho bởi hàm số \(h\left( t \right) = - 4,9{t^2} + 10t + 1,6\). Hỏi bóng ở độ cao trên 5 m trong khoảng thời gian bao nhiêu giây? (làm tròn kết quả đến hàng phần trăm).
Một quả bóng được ném thẳng lên từ độ cao 1,6 m so với mặt đất với vận tốc 10 m/s. Độ cao của bóng so với mặt đất (tính bằng mét) sau t giây được cho bởi hàm số \(h\left( t \right) = - 4,9{t^2} + 10t + 1,6\). Hỏi bóng ở độ cao trên 5 m trong khoảng thời gian bao nhiêu giây? (làm tròn kết quả đến hàng phần trăm).
Trong mặt phẳng tọa độ \(\left( {Oxy} \right),\) cho điểm \(I\left( { - 2;\;1} \right)\) và đường thẳng \(\Delta :4x + 3y + 1 = 0.\) Tìm bán kính của đường tròn có tâm \(I\) và cắt đường thẳng \(\Delta \) tại hai điểm \(A,B\) sao cho tam giác \(IAB\) vuông (kết quả làm tròn đến hàng phần trăm).
Viết phương trình tham số của đường thẳng \(d\) đi qua \(A\left( {1;1} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {2;3} \right)\).








