Bộ 5 đề thi giữa kì 2 Toán 10 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Đề 2
20 câu hỏi
Cho bảng các giá trị tương ứng của hai đại lượng \(x,y\)

Tìm mệnh đề đúng
\(y\left( 5 \right) = - 7\).
\(y\left( { - 3} \right) = 1\).
\(y\left( 8 \right) = - 3\).
\(y\left( { - 1} \right) = 3\).
Cho parabol \(\left( P \right):y = {x^2} + 4x\). Trục đối xứng của đồ thị là
\(x = - 2\).
\(x = 0\).
\(x = 2\).
\(x = 4\).
Cho \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\). Điều kiện để \(f\left( x \right) > 0,\forall x \in \mathbb{R}\) là
\(\left\{ \begin{array}{l}a > 0\\\Delta < 0\end{array} \right.\).
\(\left\{ \begin{array}{l}a > 0\\\Delta \le 0\end{array} \right.\).
\(\left\{ \begin{array}{l}a > 0\\\Delta \ge 0\end{array} \right.\).
\(\left\{ \begin{array}{l}a < 0\\\Delta > 0\end{array} \right.\).
Đường thẳng \(d\) đi qua gốc tọa độ \(O\) và có vectơ chỉ phương \(\overrightarrow u = \left( { - 1;2} \right)\) có phương trình tham số là:
\(d:\left\{ \begin{array}{l}x = - 1\\y = 2\end{array} \right.\).
\(d:\left\{ \begin{array}{l}x = - t\\y = 2t\end{array} \right.\).
\(d:\left\{ \begin{array}{l}x = 2t\\y = t\end{array} \right.\).
\(d:\left\{ \begin{array}{l}x = - 2t\\y = t\end{array} \right.\).
Xét vị trí tương đối của hai đường thẳng \({d_1}:3x - 2y - 6 = 0\) và \({d_2}:6x - 2y - 8 = 0\).
Trùng nhau.
Song song.
Vuông góc với nhau.
Cắt nhau nhưng không vuông góc.
Tâm và bán kính của đường tròn \(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = 9\) là
\(I\left( {1; - 1} \right),R = 9\).
\(I\left( {1; - 1} \right),R = 3\).
\(I\left( { - 1;1} \right),R = 3\).
\(I\left( { - 1;1} \right),R = 9\).
Trong mặt phẳng \(Oxy\), parabol \(\left( P \right)\) có phương trình chính tắc \({y^2} = 8x\) có tọa độ tiêu điểm là
\(F\left( {0;2} \right)\).
\(F\left( {2;0} \right)\).
\(F\left( {4;0} \right)\).
\(F\left( {0;4} \right)\).
Hàm số nào sau đây có đồ thị như hình bên?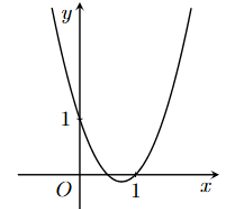
\(y = {x^2} - 3x + 1\).
\(y = - {x^2} + 3x - 1\).
\(y = - 2{x^2} + 3x - 1\).
\(y = 2{x^2} - 3x + 1\).
Tam thức bậc hai \(f\left( x \right) = {x^2} - 3x - 4\) âm khi
\(x \in \left( { - \infty ; - 1} \right] \cup \left[ {4; + \infty } \right)\).
\(x \in \left[ { - 4;2} \right]\).
\(x \in \left( { - 1;4} \right)\).
\(x \in \left( { - \infty ; - 4} \right] \cup \left[ {1; + \infty } \right)\).
Số nghiệm nguyên dương của phương trình \(\sqrt {x - 1} = x - 3\) là
\(1\).
\(3\).
\(2\).
\(0\).
Trong mặt phẳng với hệ trục tọa độ \(Oxy\), đường tròn \(\left( C \right)\) có tâm \(I\left( {1; - 2} \right)\) và tiếp xúc với trục \(Ox\) có phương trình là
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 1\).
\({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 4\).
\({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 1\).
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 4\).
Cho elip \(\left( E \right)\) đi qua 2 điểm \({A_1}\left( { - 3;0} \right),{B_1}\left( {0; - 2} \right)\). Phương trình nào là phương trình chính tắc của \(\left( E \right)\)?
\(\frac{{{x^2}}}{4} + \frac{{{y^2}}}{9} = 1\).
\(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\).
\(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{4} = 1\).
\(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{9} = 1\).
Cho đồ thị hàm số bậc hai \(y = f\left( x \right)\) như hình vẽ
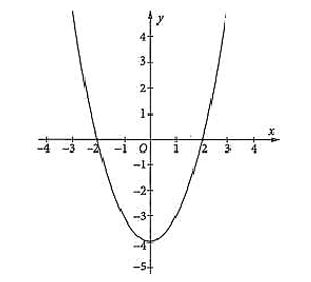
a) Hàm số đồng biến trên khoảng \(\left( { - \infty ;0} \right)\).
b) Tọa độ đỉnh của parabol là \(I\left( {0; - 4} \right)\).
c) Tam thức bậc hai \(f\left( x \right)\) có bảng xét dấu

d) \(f\left( x \right) > 0 \Leftrightarrow - 2 < x < 2\).
Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) với \(A\left( {0;3} \right),B\left( {1; - 2} \right),C\left( {5;3} \right)\). Gọi \(H\) là chân đường cao kẻ từ \(A\) xuống \(BC\). Khi đó
a) Một vectơ pháp tuyến của đường cao \(AH\) là \(\overrightarrow {CB} \).
b) Phương trình đường cao \(AH\) là \(4x + 5y - 16 = 0\).
c) Phương trình đường thẳng \(BC\) là \(5x - 4y - 13 = 0\).
d) Độ dài đường cao \(AH\) bằng \(\frac{{10}}{{\sqrt {41} }}\).
Cho hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}\frac{2}{{x - 1}},x \in \left( { - \infty ;2} \right]\\{x^2} - 1,x \in \left( {2;5} \right]\end{array} \right.\). Tính \(f\left( 3 \right)\).
Tính tổng các nghiệm của phương trình \(\sqrt {{x^2} + 2x + 4} = \sqrt {2 - x} \).
Tổng chi phí \(P\) (đơn vị: nghìn đồng) để sản xuất \(x\) sản phẩm được cho bởi biểu thức \(P = {x^2} + 30x + 3300\); giá bán một sản phẩm là \(170\) nghìn đồng. Gọi \(a;b\) lần lượt là số sản phẩm tối thiểu và tối đa mà nhà sản xuất cần sản xuất để không bị lỗ. Tính \(S = a + b\) (giả sử các sản phẩm được bán hết).
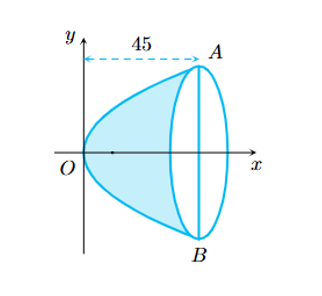
Một gương lõm có mặt cắt hình parabol (hình vẽ bên), có tiêu điểm cách đỉnh \(5\;{\rm{cm}}\). Cho biết bề sâu của gương là \(45\;{\rm{cm}}\). Tính khoảng cách \(AB\). (theo đơn vị cm).
Trong mặt phẳng \(Oxy\), cho đường tròn \(\left( C \right):{x^2} + {y^2} - 4x - 1 = 0\). Xác định tâm và bán kính của đường tròn đó.
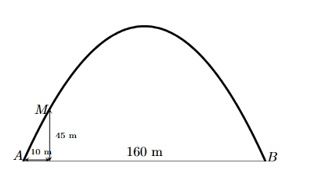
Cổng vào miền Tây (Gateway Arch) ở thành phố St.Louis, nước Mỹ, có hình dạng là một phần của parabol như hình vẽ. Khoảng cách giữa 2 chân cổng \(AB = 160\;{\rm{m}}\). Trên thành cổng, tại vị trí có độ cao 45 m so với mặt đất (tại điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10 m. Hãy tính khoảng cách từ mặt đất đến điểm cao nhất của cổng.