Bộ 5 đề thi giữa kì 2 Toán 10 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Đề 1
20 câu hỏi
Cho hàm số \(y = f\left( x \right)\) có tập xác định \(\left[ { - 3;3} \right]\) và đồ thị của nó được biểu diễn như hình dưới đây
![Cho hàm số \(y = f\left( x \right)\) có tập xác định \(\left[ { - 3;3} \right]\) và đồ thị của nó được biểu diễn như hình dưới đây (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid0-1737614150.png)
Hàm số đồng biến trên \(\left( {1;3} \right)\).
Hàm số đồng biến trên \(\left( { - 3;1} \right)\).
Hàm số đồng biến trên \(\left( { - 1;1} \right)\).
Hàm số đồng biến trên \(\left( {1;4} \right)\).
Cho \(f\left( x \right) = a{x^2} + bx + c,\left( {a \ne 0} \right)\) và \(\Delta = {b^2} - 4ac\). Cho biết dấu của \(\Delta \) khi \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\).
\(\Delta > 0\).
\(\Delta < 0\).
\(\Delta \ge 0\).
\(\Delta = 0\).
Cho phương trình \(\sqrt {2x - 3} = x - 3\). Chọn câu đúng.
\(x = 6\) là nghiệm của phương trình.
\(x = 2\) là nghiệm của phương trình.
\(x = 1\) là nghiệm của phương trình.
\(x = 3\)là nghiệm của phương trình.
Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \(d: - x + 2y + 7 = 0\). Một vectơ pháp tuyến của đường thẳng \(d\) là
\(\overrightarrow n = \left( {1;2} \right)\).
\(\overrightarrow n = \left( {2;1} \right)\).
\(\overrightarrow n = \left( {2; - 1} \right)\).
\(\overrightarrow n = \left( { - 1;2} \right)\).
Trong mặt phẳng \(Oxy\), đường thẳng \(d:x - 2y - 1 = 0\) song song với đường thẳng có phương trình nào sau đây?
\(x + 2y + 1 = 0\).
\( - x + 2y + 1 = 0\).
\(2x - y = 0\).
\( - 2x + 4y - 1 = 0\).
Phương trình đường tròn có tâm\(I\left( {a;b} \right)\) và bán kính \(R\) là
\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\).
\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = R\).
\({\left( {x + a} \right)^2} + {\left( {y + b} \right)^2} = {R^2}\).
\({\left( {x + a} \right)^2} + {\left( {y + b} \right)^2} = R\).
Phương trình nào sau đây là phương trình chính tắc của một elip?
\(\frac{{{x^2}}}{4} + \frac{{{y^2}}}{9} = 1\).
\(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 0\).
\(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\).
\(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{4} = 1\).
Tập xác định của hàm số \(y = \sqrt { - {x^2} + 2x + 3} \) là
\(\left[ { - 1;3} \right]\).
\(\left( {1;3} \right)\).
\(\left( { - \infty ; - 1} \right] \cup \left[ {3; + \infty } \right)\).
\(\left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\).
Tập nghiệm của phương trình \(\sqrt {2x + 7} = x - 4\) là
\(S = \left\{ {1;9} \right\}\).
\(S = \left\{ 1 \right\}\).
\(S = \left\{ 9 \right\}\).
\(S = \left\{ { - 1; - 9} \right\}\).
Phương trình đường thẳng đi qua hai điểm \(M\left( { - 1;0} \right),N\left( {3;1} \right)\) là
\(4x + y + 4 = 0\).
\(x - 4y - 1 = 0\).
\(4x + y - 4 = 0\).
\(x - 4y + 1 = 0\).
Cho đường tròn \(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 13\). Phương trình tiếp tuyến của \(\left( C \right)\) tại \(M\left( { - 2;5} \right)\) là:
\( - 2x + 5y + 16 = 0\).
\( - 2x + 5y - 16 = 0\).
\( - 3x + 2y - 16 = 0\).
\(3x - 2y - 16 = 0\).
Viết phương trình chính tắc của parabol đi qua điểm \(A\left( {1;4} \right)\).
\({y^2} = 8x\).
\(y = 4{x^2}\).
\({y^2} = 16x\).
\({y^2} = 32x\).
Cho hàm số bậc hai có đồ thị hàm số như hình vẽ
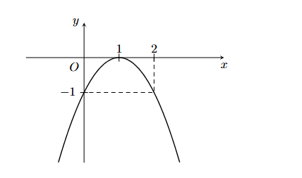
a) Tại \(x = - 1\) thì \(y = 0\).
b) Hàm số đồng biến trên khoảng \(\left( { - 1;0} \right)\).
c) Cho \(I\left( {a;b} \right)\) là đỉnh của đồ thị hàm số trên. Khi đó \(a - 2b = 1\).
d) Đồ thị biểu diễn trên là của hàm số \(y = - {x^2} + 2x - 1\).
Cho hai điểm \(A\left( {3; - 3} \right),B\left( { - 1; - 5} \right)\) và đường thẳng \(\left( d \right):4x - 3y - 2 = 0\).
a) Một vectơ pháp tuyến của đường thẳng \(d\) là \(\overrightarrow {{n_d}} = \left( {4; - 3} \right)\).
b) Đường thẳng đi qua điểm \(A\) và vuông góc với \(\left( d \right)\) có phương trình \(4x + 3y = 3\).
c) Khoảng cách từ \(A\) tới \(\left( d \right)\) nhỏ hơn khoảng cách từ \(B\) tới \(\left( d \right)\).
d) Cosin của góc tạo bởi \(\left( d \right)\) và đường thẳng \(AB\) bằng \(\frac{2}{{\sqrt 5 }}\).
Trong mặt phẳng \(Oxy\), đường tròn \(2{x^2} + 2{y^2} - 8x + 4y - 1 = 0\) có bán kính bằng bao nhiêu? (kết quả làm tròn đến hàng phần trăm).
Tập nghiệm của bất phương trình \( - {x^2} + 5x - 6 \ge 0\) có bao nhiêu giá trị nguyên?
Bảng giá cước gọi quốc tế của công ty viễn thông \(A\) được cho bởi bảng sau
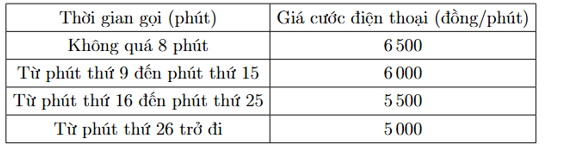
Ông An thực hiện 1 cuộc gọi quốc tế 31 phút, sau đó ông gặp sự cố bị ngắt kết nối nên ông phải thực hiện lại thêm 1 cuộc gọi quốc tế 12 phút nữa. Tổng số tiền cước ông An phải trả là bao nhiêu nghìn đồng?
Trong mặt phẳng tọa độ \(\left( {Oxy} \right)\), cho điểm \(M\left( {1; - 2} \right)\) và đường thẳng \(d:2x - 4y + 3 = 0\). Đường thẳng \(\Delta \) đi qua \(M\) và song song \(d\) có phương trình \(ax + by - 5 = 0\left( {a,b \in \mathbb{R}} \right)\). Tính giá trị biểu thức \({a^2} + {b^2}\).
Tìm tọa độ đỉnh của parabol \(y = {x^2} - 4x + 5\).
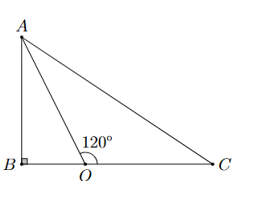
Một đài quan sát \(O\) cách ba vị trí \(A,B,C\) như hình vẽ dưới đây thỏa mãn \(OB = x\;{\rm{km}}\), \(OC = x + 1\;{\rm{km}}\) và \(OA = 2\;{\rm{km}}\). Tìm \(x\) biết khoảng cách từ vị trí \(A\) đến vị trí \(C\) gấp đôi khoảng cách từ vị trí \(A\) đến vị trí \(B\) và khoảng cách từ \(O\) đến \(B\) ngắn hơn khoảng cách từ \(O\) đến \(A\).