Bộ 5 đề thi giữa kì 2 Toán 10 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Đề 1
21 câu hỏi
Cho \(f\left( x \right) = a{x^2} + bx + c,\left( {a \ne 0} \right)\) và \(\Delta = {b^2} - 4ac\). Cho biết dấu của \(\Delta \) khi \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\).
\(\Delta > 0\).
\(\Delta < 0\).
\(\Delta \ge 0\).
\(\Delta = 0\).
Trong các bất phương trình dưới đây, bất phương trình nào là bất phương trình bậc hai một ẩn \(x\)?
\(x + 3 \ge 0\).
\( - {x^2} + 3x - 2 \ge 0\).
\({x^2} - x - 3 \ne 0\).
\(3{x^2} - 3\sqrt x - 3 > 0\).
Cho phương trình \(\sqrt {2x - 3} = x - 3\). Chọn câu đúng.
\(x = 6\) là nghiệm của phương trình.
\(x = 2\) là nghiệm của phương trình.
\(x = 1\) là nghiệm của phương trình.
\(x = 3\)là nghiệm của phương trình.
Trong mặt phẳng với hệ \(Oxy\), cho \(\overrightarrow {OM} = 7\overrightarrow i + 4\overrightarrow j \), tìm tọa độ của điểm \(M\)
\(M\left( {7;4} \right)\).
\(M\left( {4;7} \right)\).
\(M\left( { - 7; - 4} \right)\).
\(M\left( {7; - 4} \right)\).
Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \(d: - x + 2y + 7 = 0\). Một vectơ pháp tuyến của đường thẳng \(d\) là
\(\overrightarrow n = \left( {1;2} \right)\).
\(\overrightarrow n = \left( {2;1} \right)\).
\(\overrightarrow n = \left( {2; - 1} \right)\).
\(\overrightarrow n = \left( { - 1;2} \right)\).
Phương trình đường tròn có tâm\(I\left( {a;b} \right)\) và bán kính \(R\) là
\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\).
\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = R\).
\({\left( {x + a} \right)^2} + {\left( {y + b} \right)^2} = {R^2}\).
\({\left( {x + a} \right)^2} + {\left( {y + b} \right)^2} = R\).
Phương trình nào sau đây là phương trình chính tắc của một elip?
\(\frac{{{x^2}}}{4} + \frac{{{y^2}}}{9} = 1\).
\(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 0\).
\(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\).
\(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{4} = 1\).
Tập nghiệm của bất phương trình \(2{x^2} - 7x - 15 \ge 0\) là
\(\left( { - \infty ; - \frac{3}{2}} \right] \cup \left[ {5; + \infty } \right)\).
\(\left[ { - \frac{3}{2};5} \right]\).
\(\left( { - \infty ; - 5} \right] \cup \left[ {\frac{3}{2}; + \infty } \right)\).
\(\left[ { - 5;\frac{3}{2}} \right]\).
Tập nghiệm của phương trình \(\sqrt {2x + 7} = x - 4\) là
\(S = \left\{ {1;9} \right\}\).
\(S = \left\{ 1 \right\}\).
\(S = \left\{ 9 \right\}\).
\(S = \left\{ { - 1; - 9} \right\}\).
Phương trình đường thẳng đi qua hai điểm \(M\left( { - 1;0} \right),N\left( {3;1} \right)\) là
\(4x + y + 4 = 0\).
\(x - 4y - 1 = 0\).
\(4x + y - 4 = 0\).
\(x - 4y + 1 = 0\).
Cho đường tròn \(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 13\). Phương trình tiếp tuyến của \(\left( C \right)\) tại \(M\left( { - 2;5} \right)\) là:
\( - 2x + 5y + 16 = 0\).
\( - 2x + 5y - 16 = 0\).
\( - 3x + 2y - 16 = 0\).
\(3x - 2y - 16 = 0\).
Viết phương trình chính tắc của parabol đi qua điểm \(A\left( {1;4} \right)\).
\({y^2} = 8x\).
\(y = 4{x^2}\).
\({y^2} = 16x\).
\({y^2} = 32x\).
Cho hàm số \(f\left( x \right) = 20{x^2} + 56x + 36\).
a) Theo đề bài thì \(f\left( x \right)\) là một tam thức bậc hai.
b) Bất phương trình \(f\left( x \right) \ge 0 \Leftrightarrow \left( { - \infty ; - \frac{7}{5}} \right) \cup \left( { - 1; + \infty } \right)\).
c) Bất phương trình \(f\left( x \right) \le 0 \Leftrightarrow x \in \left( { - \frac{9}{5}; + \infty } \right)\).
d) Bất phương trình luôn nhận giá trị không âm với mọi \(x \in \mathbb{R}\).
Cho hai điểm \(A\left( {3; - 3} \right),B\left( { - 1; - 5} \right)\) và đường thẳng \(\left( d \right):4x - 3y - 2 = 0\).
a) Một vectơ pháp tuyến của đường thẳng \(d\) là \(\overrightarrow {{n_d}} = \left( {4; - 3} \right)\).
b)Ta có \(\overrightarrow {OA} = 3\overrightarrow j - 3\overrightarrow i \).
c) Khoảng cách từ \(A\) tới \(\left( d \right)\) nhỏ hơn khoảng cách từ \(B\) tới \(\left( d \right)\).
d) Cosin của góc tạo bởi \(\left( d \right)\) và đường thẳng \(AB\) bằng \(\frac{2}{{\sqrt 5 }}\).
Trong mặt phẳng \(Oxy\), đường tròn \(2{x^2} + 2{y^2} - 8x + 4y - 1 = 0\) có bán kính bằng bao nhiêu? (kết quả làm tròn đến hàng phần trăm).
Tập nghiệm của bất phương trình \( - {x^2} + 5x - 6 \ge 0\) có bao nhiêu giá trị nguyên?
Trên màn hình ra đa của đài kiểm soát không lưu (được coi như mặt phẳng tọa độ \(Oxy\) với đơn vị trên các trục tính theo kilômét), một máy bay trực thăng chuyển động thẳng đều từ thành phố A có tọa độ (600; 200) đến thành phố B có tọa độ (200; 500) và thời gian bay quãng đường AB là 3 giờ. Hãy tìm tung độ của máy bay trực thăng tại thời điểm sau khi xuất phát 1 giờ.
Trong mặt phẳng tọa độ \(\left( {Oxy} \right)\), cho điểm \(M\left( {1; - 2} \right)\) và đường thẳng \(d:2x - 4y + 3 = 0\). Đường thẳng \(\Delta \) đi qua \(M\) và song song \(d\) có phương trình \(ax + by - 5 = 0\left( {a,b \in \mathbb{R}} \right)\). Tính giá trị biểu thức \({a^2} + {b^2}\).
Tìm tất cả các giá trị của tham số \(m\) để biểu thức \(f\left( x \right) = \left( {m - 2024} \right){x^2} + 2mx + 3\) là một tam thức bậc hai.
Một đài quan sát \(O\) cách ba vị trí \(A,B,C\) như hình vẽ dưới đây thỏa mãn \(OB = x\;{\rm{km}}\), \(OC = x + 1\;{\rm{km}}\) và \(OA = 2\;{\rm{km}}\). Tìm \(x\) biết khoảng cách từ vị trí \(A\) đến vị trí \(C\) gấp đôi khoảng cách từ vị trí \(A\) đến vị trí \(B\) và khoảng cách từ \(O\) đến \(B\) ngắn hơn khoảng cách từ \(O\) đến \(A\).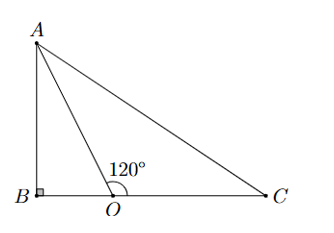
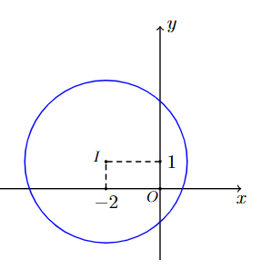
Hình vẽ bên mô phỏng một trạm thu phát sóng điện thoại di động đặt ở vị trí \(I\) có tọa độ \(\left( { - 2;1} \right)\) trong mặt phẳng tọa độ (đơn vị trên hai trục là kilômét). Tính theo đường chim bay, xác định khoảng cách ngắn nhất để một người ở vị trí có tọa độ \(\left( { - 3;4} \right)\) di chuyển được tới vùng phủ sóng theo đơn vị kilômét (làm tròn kết quả đến hàng phần trăm). Biết rằng trạm thu phát sóng đó được thiết kế với bán kính phủ sóng 3 (km).