Bộ 5 đề thi giữa kì 1 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 3
21 câu hỏi
Trong các số \(0,16;{\rm{ }} - 1\frac{2}{3};{\rm{ }}\frac{{ - 5}}{{ - 13}};{\rm{ }}0;{\rm{ 5; }}\frac{{25}}{4}\) có bao nhiêu số hữu tỉ dương?
1.
2.
3.
4.
Cho hai số hữu tỉ \(a\) và \(b\) được biểu diễn trên trục số như sau:

Chọn khẳng định đúng.
\(b > 0 > a.\)
\(b > a > 0.\)
\(b < a < 0.\)
\(b < 0 < a.\)
Giá trị của \({\left( {\frac{3}{5}} \right)^3}\) bằng
\(\frac{9}{{15}}.\)
\(\frac{{27}}{{125}}.\)
\(\frac{{ - 9}}{{15}}.\)
\(\frac{{ - 27}}{{125}}.\)
Thực hiện bỏ ngoặc biểu thức \(\left( {a + b} \right) - \left( {b - c - 1} \right)\) ta được
\(a - c - 1.\)
\(a + c + 1.\)
\(a + 2b + c + 1.\)
\(a + c - 1.\)
Số \(\sqrt 5 \) là
Số tự nhiên.
Số nguyên.
Số hữu tỉ.
Số vô tỉ.
Khẳng định nào sau đây là sai?
\(\sqrt {{{\left( { - 5} \right)}^2}} = - 5.\)
\(\sqrt {25} = 5.\)
\( - \sqrt 9 = - 3.\)
\(\sqrt {{x^2}} = \left| x \right|.\)
Khẳng định nào sau đây là đúng?
Hình lập phương có 8 đỉnh, 12 cạnh và 4 đường chéo.
Hình lập phương có 12 đỉnh, 8 cạnh và 4 đường chéo.
Hình lập phương có 8 đỉnh, 12 cạnh và 6 đường chéo.
Hình lập phương có 12 đỉnh, 8 đỉnh và 6 đường chéo.
Các mặt bên của hình lăng trụ đứng tứ giác là
Các hình bình hành.
Các hình chữ nhật.
Các hình vuông.
Các hình thang cân.
Cho hình lăng trụ đứng tứ giác như hình bên. Khẳng định nào sau đây là sai?
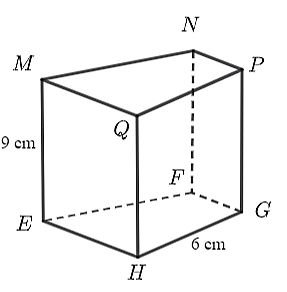
\(PG = 9{\rm{ cm}}{\rm{.}}\)
\(EH = 9{\rm{ cm}}{\rm{.}}\)
\(PQ = 6{\rm{ cm}}{\rm{.}}\)
Mặt đáy của lăng trụ đứng là tứ giác \(MNPQ.\)
Thể tích của hình hộp chữ nhật có chiều dài là \(a,\) chiều rộng là \(b,\) chiều cao là \(h\) (các kích thước cùng đơn vị đo) là
\(V = 2.\left( {a + b} \right).h\).
\(V = a.b.h.\)
\(V = 2.a.b.h.\)
\(V = \left( {a + b} \right).h.\)
Cho hình vẽ bên. Một góc kề của \(\widehat {bOc}\) là
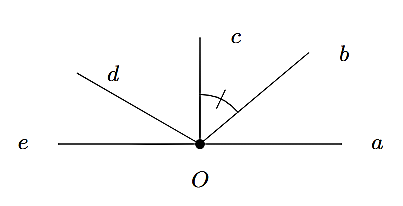
\(\widehat {dOe}.\)
\(\widehat {aOd}.\)
\(\widehat {aOb}.\)
\(\widehat {eOb}.\)
Khẳng định nào sau đây là đúng?
Hai góc đối đỉnh thì bù nhau.
Hai góc đối đỉnh thì bằng nhau.
Hai góc bằng nhau thì đối đỉnh.
Hai góc đối đỉnh thì phụ nhau.
Giá niêm yết của một thùng sữa milo là \(320{\rm{ 000}}\) đồng. Nhân ngày 1/6 cửa hàng giảm giá \(5\% \)/thùng và giảm thêm \(2\% \)/thùng trên giá niêm yết cho khách hàng thứ \(300\) của cửa hàng.
a) Số tiền 299 vị khách đầu tiên được giảm là \(16{\rm{ 000}}\) đồng.
b) Số tiền vị khách thứ 300 được giảm là \(23{\rm{ 000}}\) đồng.
c) Số tiền vị khách thứ 300 phải thanh toán khi mua thùng sữa trên nhỏ hơn \(300{\rm{ 000}}\) đồng.
d) Vị khách thứ 300 tiết kiệm được \(7{\rm{ }}000\) đồng so với khách hàng mua sữa khác.
Cho hình lăng trụ đứng tứ giác \(ABCD.A'B'C'D'\) có đáy là hình thang vuông như hình vẽ dưới đây.
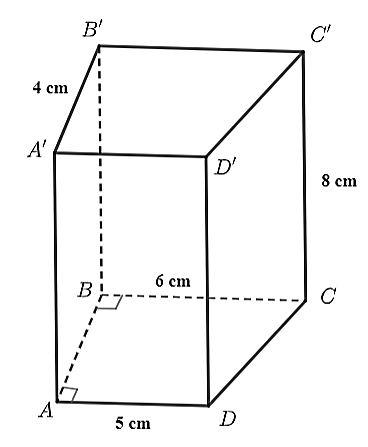
a) Các mặt đáy của hình lăng trụ là \(ABCD\) và \(A'B'C'D'\).
b) \(AB = A'B' = 4{\rm{ cm}}{\rm{.}}\)
c) Diện tích một đáy của hình lăng trụ là \(44{\rm{ c}}{{\rm{m}}^2}.\)
d) Thể tích của hình lăng trụ đó là \(352{\rm{ c}}{{\rm{m}}^3}.\)
Tìm giá trị của \(x,\) biết: \(\frac{2}{3}:x + \frac{1}{2} = \frac{4}{3}\) (kết quả ghi dưới dạng số thập phân).
Số đối của \( - \sqrt {\frac{{81}}{{16}}} \) là bao nhiêu (kết quả ghi dưới dạng số thập phân)?
Một hình lăng trụ đứng tam giác có độ dài cạnh bên bằng \(10{\rm{ cm,}}\) đáy là tam giác có độ dài một cạnh và chiều cao tương ứng lần lượt là \(3{\rm{ cm}}\) và \(5{\rm{ cm}}{\rm{.}}\) Tính thể tích của hình lăng trụ đứng tam giác đó. (đơn vị: cm3).
Cho \(\widehat {xOy} = 80^\circ \) và tia \(Oz\) nằm giữa hai tia \(Ox,Oy\) sao cho \(\widehat {yOz} = 40^\circ \). Vẽ tia \(Om\) là tia đối của tia \(Ox\). Hỏi góc \(mOz\) có số đo bằng bao nhiêu độ?
(1,5 điểm) Thực hiện phép tính:
a) \(\frac{{31}}{{23}} - \left( {\frac{7}{{32}} + \frac{8}{{23}}} \right)\);
b) \(\left( {1 - \frac{2}{3} - \frac{1}{4}} \right):{\left( {\frac{4}{5} - \frac{3}{4}} \right)^2}\);
c) \({\left( { - \frac{1}{2}} \right)^2}.\frac{2}{3} + \sqrt {81} .\left( {\frac{{ - 2}}{3}} \right) + 1\frac{1}{2}.\sqrt {\frac{4}{9}} \).
(1,0 điểm) Một chiếc bánh ngọt có dạng hình lăng trụ đứng tam giác có kích thước như hình dưới đây.
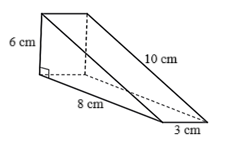
Người ta đặt chiếc bánh ngọt lên một tấm bìa cứng và muốn phủ một lớp kem lên toàn bộ các mặt của chiếc bánh. Biết mỗi cm2 kem cần \(0,25\) gam kem, mỗi gam kem có giá \(500\) đồng. Hỏi phủ kem chiếc bánh như vậy tốn hết bao nhiêu tiền?
(0,5 điểm) Cho \(\frac{1}{2}A = \frac{1}{{{3^2}}} + \frac{1}{{{5^2}}} + \frac{1}{{{7^2}}} + \frac{1}{{{9^2}}} + ... + \frac{1}{{{{2025}^2}}}\). Chứng minh rằng \(A < \frac{{506}}{{1013}}\).








