Bộ 5 đề thi cuối kì 1 Toán 8 Kết nối tri thức cấu trúc mới có đáp án - Đề 5
21 câu hỏi
Đa thức \(A = {x^2} + 2{y^5} - {x^4}{y^4} - 1\) có bao nhiêu hạng tử?
3.
4.
5.
6.
Cho các đơn thức \(A = \left( {0,3 + \pi } \right){x^2}y;\) \(B = \frac{1}{2}xy{x^2}z;\) \(C = - xyx{z^2}\) và \(D = \left( {\sqrt 2 + 1} \right)x{y^2}z.\) Hai đơn thức thu gọn trong các đơn thức đã cho là
\(A\) và \(B.\)
\(B\) và \(C.\)
\(A\) và \(D.\)
\(A\) và \(C.\)
Khẳng định nào sau đây là sai?
\({\left( {x + y} \right)^2} = {x^2} + 2xy + {y^2}\).
\({\left( {x + y} \right)^3} = {x^3} + 3{x^2}y + 3x{y^2} + {y^3}\).
\({x^3} - {y^3} = \left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)\).
\({\left( {x - y} \right)^3} = {x^3} - {y^3}\).
Với mọi giá trị \(x \in \mathbb{R}\) thì giá trị của biểu thức \({x^2} - 20x + 101\) là một số
dương.
không âm.
không dương.
âm.
Nhận định nào sau đây là sai?
Hình vuông là hình chữ nhật có hai cạnh bên bằng nhau.
Hình vuông là hình chữ nhật nhưng không là hình thoi.
Trong hình chữ nhật có hai đường chéo cắt nhau tại trung điểm mỗi đường.
Hình vuông có hai đường chéo là phân giác các góc trong hình vuông.
Hình bình hành \[ABCD\;\] là hình chữ nhật khi
\[AB = AD.\]
\(\widehat A = 90^\circ .\)
\[AB = 2AC\].
\(\widehat A = \widehat C.\)
Cho hình vẽ bên, biết \(BC\parallel ED\). Khẳng định nào sau đây là sai?
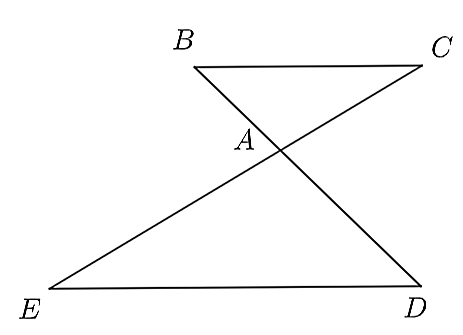
\(\frac{{AB}}{{AD}} = \frac{{BC}}{{DE}}.\)
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}.\)
\(\frac{{AB}}{{DB}} = \frac{{AC}}{{CE}} = \frac{{BC}}{{DE}}.\)
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}.\)
Cho tam giác \(ABC\) có \[BM\] là tia phân giác của \(\widehat {ABC}\,\,\left( {M \in AC} \right)\) thì
\(\frac{{AB}}{{BC}} = \frac{{MC}}{{MB}}\).
\(\frac{{AB}}{{BC}} = \frac{{MC}}{{AC}}\).
\(\frac{{AB}}{{BC}} = \frac{{MA}}{{MC}}\).
\(\frac{{AB}}{{BC}} = \frac{{MA}}{{AC}}\).
Dữ liệu về số người trong mỗi nhà của các nhà gần nhà em thuộc loại dữ liệu nào trong các loại dữ liệu sau?
Dữ liệu số rời rạc.
Dữ liệu không là số có thể sắp thứ tự.
Dữ liệu số liên tục.
Dữ liệu không là số không thể sắp thứ tự.
Để biểu diễn tỉ lệ của các phần trong tổng thể ta dùng biểu đồ nào sau đây?
Biểu đồ hình quạt tròn.
Biểu đồ cột tranh.
Biểu đồ đoạn thẳng.
Biểu đồ cột.
Cho biểu đồ sau:
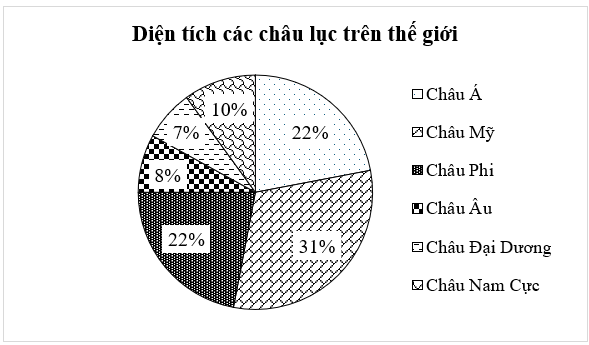
Hỏi châu Mỹ chiếm bao nhiêu phần trăm tổng diện tích của cả sau châu lục đó?
\(20\% .\)
\(30\% .\)
\(28\% .\)
\(7\% .\)
Biểu đồ đoạn thẳng dưới đây biểu diễn sản lượng thủy sản của nước ta qua các năm 2010; 2014; 2016; 2018; 2020 (đơn vị: nghìn tấn).
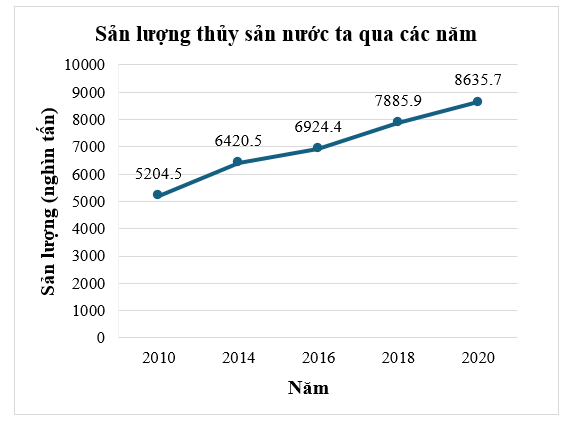
(Nguồn: Niên giám thống kê 2021)
Hỏi sản lượng thủy sản của nước ta năm 2020 chiếm bao nhiêu phần trăm tổng sản lượng thủy sản của nước ta qua các năm? (Kết quả làm tròn đến hàng phần mười)
\(22,4\% \).
\(19,7\% \).
\(24,6\% \).
\(14,8\% \).
Cho hai đa thức:
\[R = \left( {xy - 4{x^2} + 2} \right) \cdot x{y^2}\] và \[T = \left( {15{x^3}{y^4} - 20{x^4}{y^3} + 10{x^2}{y^3}} \right):5xy.\]
Đa thức \(S\) thỏa mãn \(R = T - S.\)
a) Hệ số tự do của đa thức \(R\) là 2.
b) Bậc của đa thức \(T\) là 3.
c) Giá trị của biểu thức \(T\) tại \[x = 1\,;\,\,y = - 1\] là \( - 5\).
d) \(S\) là một đơn thức.
Cho \(\Delta ABC\), trung tuyến \(AM\), đường phân giác của \(\widehat {AMB}\) cắt \(AB\) ở \(D\), đường phân giác \(\widehat {AMC}\) cắt \(AC\) ở \(E.\) Gọi \(I\) là giao điểm của \(AM\) và \(DE\). Biết \(BC = 30{\rm{ cm, }}AM = 10{\rm{ cm}}{\rm{.}}\)
a) \(\frac{{BD}}{{AD}} = \frac{{MB}}{{MA}}.\)
b) \(DE\parallel BC\).
c) \(DI = EI.\)
d) \(ED = 6{\rm{ cm}}{\rm{.}}\)
Cho biểu thức \(S = {\left( {x + 5} \right)^2} - {\left( {x + 2} \right)^2} - 6x\). Giá trị của biểu thức \(S\) bằng bao nhiêu?
Có bao nhiêu giá trị của \(x\) thỏa mãn \({x^3}--2{x^2} + x = 0?\)
Tìm \(x\) trong hình vẽ dưới đây theo đơn vị độ.
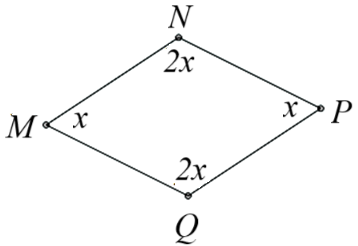
Cho hình vẽ với các số liệu sau đây:
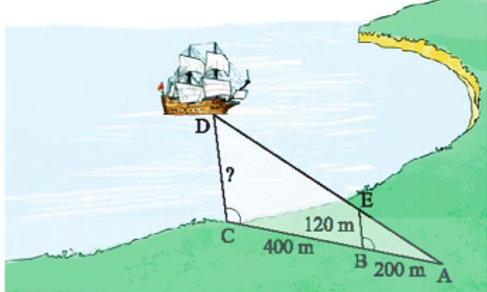
Tính khoảng cách \(CD\) từ con tàu đến trạm quan trắc đặt tại điểm \(C\) theo đơn vị m.
(1,5 điểm) Doanh thu (đơn vị: tỉ đồng) của hai chi nhánh công ty A trong năm 2023 và 2024 được cho trong bảng sau:
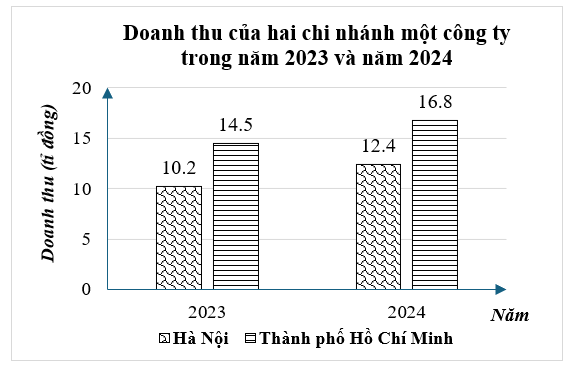
a) Lập bảng thống kê doanh thu của hai chi nhánh này trong năm 2021 và năm 2022 từ biểu đồ trên.
b) Trong hai năm trên, tổng doanh thu của năm nào lớn hơn và lớn hơn bao nhiêu?
c) Chi phí hoạt động năm 2024 của Hà Nội chiếm 70%, Thành phố Hồ Chí Minh chiếm 60%. Hỏi chi nhánh nào có lợi nhuận cao hơn và hơn bao nhiêu? Biết lợi nhuận bằng doanh thu trừ đi chi phí.
(1,0 điểm) Cho tam giác \(ABC\) có \(AB < AC,\) \(AI\) là đường cao và ba điểm \(D,\,\,\,E,\,\,\,F\) theo thứ tự là trung điểm của các đoạn thẳng \(AB,\,\,\,AC,\,\,\,BC.\) Lấy điểm \(J\) sao cho \(E\) là trung điểm \[IJ.\]
a) Chứng minh tứ giác \(DEFI\) là hình thang cân.
b) \(EB\) và \(FD\) cắt nhau tại \(K.\) Chứng minh hai tứ giác \(ADKE\) và \(KECF\) có diện tích bằng nhau.
(0,5 điểm) Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất, cọc cao \(2\,\,{\rm{m}}\) và đặt xa cây \(4\,\,{\rm{m}}.\) Sau khi người ấy lùi ra xa cách cọc \(0,5\,\,{\rm{m}}\) thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng (như hình vẽ). Hỏi cây cao bao nhiêu, biết khoảng cách từ chân đến mắt người ấy là \(1,7\,\,{\rm{m}}.\)