Bộ 10 đề thi giữa kì 1 Toán 8 Kết nối tri thức có đáp án - Đề 7
38 câu hỏi
Trong các biểu thức đại số sau, biểu thức nào là đơn thức?
\(\frac{{2x}}{y}\).
\(3x + 2y\).
\(4\left( {x - y} \right)\).
\( - \frac{2}{3}x{y^2}\).
Khi nhân đa thức \(M + N\) với đa thức \(P\)ta được kết quả là
\[MP + NP\].
\[MP + N\].
\[MN + NP\].
\[M + NP\].
Cho các đơn thức \(A = 4{x^3}y\left( { - 5xy} \right)\), \(B = {x^4}{y^2}\), \(C = - 5{x^2}{y^4}\). Các đơn thức nào sau đây đồng dạng với nhau?
Đơn thức \(A\) và đơn thức \(C\).
Đơn thức \(B\) và đơn thức \(C\).
Đơn thức \(A\) và đơn thức \(B\).
Cả ba đơn thức \(A,B,C\) đồng dạng với nhau.
Cho biểu thức \(H = \left( {2x - 3} \right)\left( {x + 7} \right) - 2x\left( {x + 5} \right) - x\). Khẳng định nào sau đây là đúng?
\(H = 21 - x\).
\(H < - 1\).
\(10 < H < 20\).
\(H > 0\).
Chọn câu trả lời đúng nhất để điền vào chỗ chấm: \({\left( {M - N} \right)^2} = ...\)
\({\left( {N - M} \right)^2}\).
\({M^2} - 2MN + {N^2}\).
\({N^2} - 2NM + {M^2}\).
Cả A, B, C đều đúng.
Đa thức \(14{x^2}y - 21x{y^2} + 28{x^2}{y^2}\) được phân tích thành
\(7xy\left( {2x - 3y + 4xy} \right)\).
\(xy\left( {14x - 21y + 28xy} \right)\).
\(7{x^2}y\left( {2 - 3y + 4xy} \right)\).
\(7x{y^2}\left( {2x - 3y + 4x} \right)\).
Trong các tứ giác sau đây, tứ giác nào không phải là tứ giác lồi?
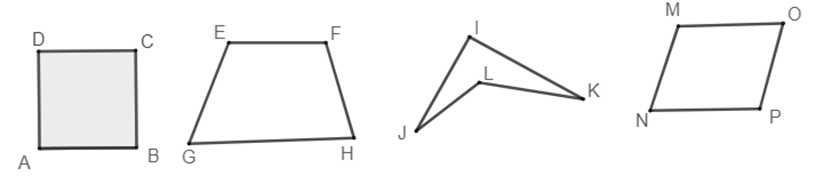
Tứ giác \(ABCD.\)
Tứ giác \(EFHG.\)
Tứ giác \(IJLK.\)
Tứ giác \(MNPO.\)
Tổng số đo các góc trong tứ giác bằng
\(90^\circ \).
\(120^\circ \).
\(180^\circ \).
\(360^\circ \).
Tứ giác \(ABCD\) có \(\widehat A = 100^\circ ,\) góc ngoài tại đỉnh \(B\) bằng \(110^\circ ;\,\,\widehat C = 75^\circ .\) Số đo góc \(D\) là
\(45^\circ \).
\(115^\circ \).
\(75^\circ \).
\(110^\circ \).
Hình bình hành là hình chữ nhật khi
có hai đường chéo bằng nhau.
có hai cạnh kề bằng nhau.
có hai đường chéo cắt nhau tại trung điểm mỗi đường.
có hai cạnh đối bằng nhau.
Trong các khẳng định sau, khẳng định nào sai?
Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
Hình thang có hai cạnh bên song song là hình bình hành.
Hình thang có hai đường chéo bằng nhau là hình bình hành.
Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Tứ giác \[ABCD\]trong hình vẽ bên là 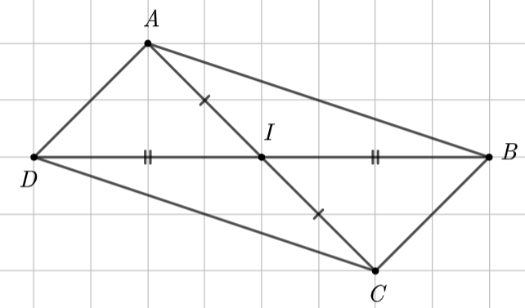
hình vuông.
hình chữ nhật.
hình thoi.
hình bình hành
Cho hai đa thức \(A = {x^2} - 4xy - 4\) và \(B = 2{x^2} - 3xy + {y^2} - 4.\)
Đa thức \(M\) và \(P\) thỏa mãn \(B = A + M\,;\, & P = \left( {x - 3} \right)M - y - \left( {x + y} \right)\left( {xy - 3y} \right).\)
a) Hạng tử tự do của đa thức \(A\) là \( - 4\).
b) Với \(x = 1\,;\,\,y = 0\) thì giá trị của biểu thức \(B\) bằng \( - 2.\)
c) \(M = {x^2} + 7xy + {y^2}.\)
d) Giá trị của biểu thức \(P\) không phụ thuộc vào biến \(y\).
Cho tam giác \(ABC\) vuông tại \(A\). Gọi \(M\) là một điểm bất kì trên cạnh huyền \(BC\). Gọi \(D\) và \(E\) lần lượt là chân đường vuông góc kẻ từ \(M\) xuống \(AB\) và \(AC.\)Lấy điểm \(I\) sao cho \(A\) là trung điểm của \(ID\); điểm \(K\) sao cho \(M\) là trung điểm của \(EK\).
a) \(IA = ID\,;\,\,KM = KE.\) b) Tứ giác \(ADME\) là hình chữ nhật.
c) Tứ giác \(ADMC\) là hình thang cân. d) \(DK\,{\rm{//}}\,EI\).
Cho đa thức \(A = - \frac{1}{3}x{y^2} + \frac{1}{2}{x^2}y + x{y^2} - \frac{3}{4}{x^2}y.\) Tính giá trị của \(A\) tại \(x = - 2;y = 3\).
Để biểu thức \[{x^3} + 6{x^2} + 12x + m\] là lập phương của một tổng thì giá trị của\(m\) là bao nhiêu?
Tứ giác \(ABCD\) có \(\widehat {A\,\,} = 65^\circ ,\)\(\widehat {B\,} = \widehat C + 23^\circ ,\)\(\widehat {D\,} = 58^\circ .\)Tính số đo góc \(C\)(đơn vị: độ).
Cho hình vuông \[ABCD\], hai đường chéo \[AC\] cắt \[BD\] tại điểm \[O.\]Tính số đo của góc của tam giác \[OAB\] (đơn vị: độ)
Phân tích mỗi đa thức sau thành nhân tử:
a) \(3{x^2} - \sqrt 3 x + \frac{1}{4}\); b) \[{x^4} + {x^3} + 2{x^2} + x + 1\]; c) \({x^3} + 2{x^2} + x - 16x{y^2}\).
Cho tam giác \[ABC\] cân tại \[A,{\rm{ }}AH\] là đường cao. Gọi \[M,{\rm{ }}N\] lần lượt là trung điểm của \[AB,{\rm{ }}AC\]. Gọi \[D,{\rm{ }}E\] lần lượt là điểm sao cho \[M\] là trung điểm của \[HD,{\rm{ }}N\] là trung điểm của \[HE.\]
a) Chứng minh \[AHBD,{\rm{ }}AHCE,{\rm{ }}BCED\] là những hình chữ nhật.
b) Chứng minh \[BE = CD,\,\,DH = HE.\]
c) Chứng minh giao điểm của \[BE\] và \[CD\] là trung điểm của \[AH\].
Đa thức nào sau đây chưa thu gọn?
\[4{x^2} + x - y\];
\[{x^4}y + x - 2y{x^4}\];
\[ - {x^3}y + \frac{2}{5}{y^2}\];
\[\frac{{x + 2y}}{5}\].
Đa thức nào sau đây không phải là đa thức bậc 4?
\(4x{y^2}z\);
\({x^4} - {3^5}\);
\(x{y^2} + xyzt\);
\({x^4} - \frac{1}{2}x{y^3}z\).
Cho các đơn thức \(A = 4{x^3}y\left( { - 5xy} \right)\), \(B = {x^4}{y^2}\), \(C = - 5{x^2}{y^4}\). Các đơn thức nào sau đây đồng dạng với nhau?
Đơn thức \(A\) và đơn thức \(C\);
Đơn thức \(B\) và đơn thức \(C\);
Đơn thức \(A\) và đơn thức \(B\);
Cả ba đơn thức \(A,B,C\) đồng dạng với nhau.
Giá trị của biểu thức \(S = - 6xy\frac{1}{2}{x^2}yz + 2zx{y^2}{x^2}\) khi \(x = - 2,y = 1,z = - 1\) là
\(S = 8\);
\(S = - 8\);
\(S = - 4\);
\(S = 4\).
Đẳng thức nào sau đây là hằng đẳng thức?
\({x^2} - x = - x + {x^2}\);
\(x\left( {x - 1} \right) = x - {x^2}\);
\({\left( {a - b} \right)^2} = - {\left( {b - a} \right)^2}\);
\(a - 2 = 2 - a\).
Chọn đẳng thức sai trong các đẳng thức sau đây:
\({\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\);
\({\left( { - a - b} \right)^3} = - {a^3} - 3{a^2}b - 3a{b^2} - {b^3}\);
\({\left( { - a + b} \right)^3} = - {a^3} - 3{a^2}b + 3a{b^2} + {b^3}\);
\({\left( {a - b} \right)^3} = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\).
Cho tứ giác \(ABCD\). Khẳng định nào sau đây là sai?
\(AB\) và \(BC\) là hai cạnh kề nhau;
\(BC\) và \(AD\) là hai cạnh đối nhau;
\(\widehat A\) và \(\widehat B\) là hai góc đối nhau;
\(AC\) và \(BD\) là hai đường chéo.
Khẳng định nào sau đây là đúng?
Tứ giác có 4 đường chéo;
Tổng các góc của một tứ giác bằng \(180^\circ \);
Tồn tại một tứ giác có 1 góc tù và 3 góc vuông;
Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của tứ giác đó.
Cho tứ giác \(ABCD\) có \(\widehat {C\,} = 60^\circ ,\widehat {D\,} = 80^\circ ,\widehat {A\,\,} - \widehat {B\,} = 10^\circ .\) Số đo của \(\widehat {A\,}\) là
\(95^\circ \);
\(105^\circ \);
\(115^\circ \);
\(125^\circ \).
Khẳng định nào sau đây là sai?
Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
Hình thang có hai cạnh bên song song là hình bình hành.
Hình thang có hai đường chéo bằng nhau là hình bình hành.
Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Khẳng định nào sau đây là sai? Tứ giác \[ABCD\] là hình chữ nhật khi
\(\widehat {A\,} = \widehat B = \widehat C = 90^\circ ;\)
\(\widehat {A\,} = \widehat B = \widehat C = 90^\circ \) và \[AB\,{\rm{//}}\,CD;\]
\[AB = CD = AD = BC;\]
\[AB\,{\rm{//}}\,CD;{\rm{ }}AB = CD;{\rm{ }}AC = BD.\]
Các dấu hiệu nhận biết sau, dấu hiệu nào không đủ để kết luận một hình vuông?
Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông;
Hình thoi có một góc vuông là hình vuông;
Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông;
Hình thoi có hai đường chéo vuông góc là hình vuông.
Thu gọn biểu thức:
a) \(\frac{3}{4}{x^3}{y^3}:\left( { - \frac{1}{2}{x^2}{y^2}} \right);\) b) \[3xy \cdot \left( {2{x^2}--3yz + {x^3}} \right);\]
c) \(\left( {4{x^4} - 8{x^2}{y^2} + 12{x^5}y} \right):\left( { - 4{x^2}} \right) + 3{x^3}y;\) d) \(y\left( {3{y^2} - {x^3}} \right) + \left( {{x^2} + 3y} \right)\left( {xy - {y^2}} \right).\)
Tìm \(x,\) biết:
a) \[{x^3} + 9{x^2} + 27x + 19 = 0;\] b) \[25{\left( {x + 3} \right)^2} + \left( {1--5x} \right)\left( {1 + 5x} \right) = 8.\]
Cho hai đa thức \(A = {x^2} - 4xy - 4\) và \(B = 2{x^2} - 3xy + {y^2} - 4.\) Tìm đa thức \(M\) thỏa mãn \(B = A + M.\)
Chứng minh giá trị của biểu thức sau không phụ thuộc vào giá trị của biến \(y:\)
\[P = \left( {x - 3} \right)M - y - \left( {x + y} \right)\left( {xy - 3y} \right).\]
Cho hình bình hành \[ABCD\] có cạnh \(AB = 2AD.\) Gọi \[M,{\rm{ }}N\] lần lượt là trung điểm của \[AB\] và \[CD.\]
a) Chứng minh rằng \(DMBN\) là hình bình hành.
b) Chứng minh rằng \(AN\) là tia phân giác của góc \[DAB.\]
c) Gọi giao điểm của \(AN\) với \[DM\]là \[P,{\rm{ }}CM\] với \[BN\] là \[Q.\] Tìm điều kiện của hình bình hành\[ABCD\] để tứ giác \[PMQN\] là hình vuông.
Cho \(x,y,z\) là ba số thỏa mãn điều kiện:
\(4{x^2} + 2{y^2} + 2{z^2} - 4xy - 4xz + 2yz - 6y - 10z + 34 = 0.\)
Tính giá trị của biểu thức \(S = {\left( {x - 4} \right)^{2023}} + {\left( {y - 4} \right)^{2025}} + {\left( {z - 4} \right)^{2027}}.\)








