Bộ 10 đề thi Giữa kì 2 Toán 9 Cánh diều cấu trúc mới có đáp án - Đề 02

Biểu đồ tần số sau đây biểu diễn số học sinh khối 9 đến thư viện của trường mượn sách vào các ngày trong tuần:

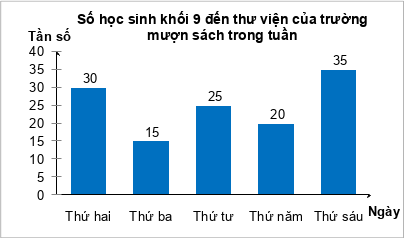
Ngày nào trong tuần có 15 học sinh đến mượn sách của thư viện?

Cho là một trong các giá trị khác nhau của mẫu dữ liệu cỡ Biết rằng tần số của giá trị này là  Khi đó tần số tương đối của giá trị là

Sắp xếp các thứ tự sau để được các bước tính xác suất của biến cố hoàn chỉnh:

(1) Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.

(2) Mô tả không gian mẫu của một phép thử, từ đó tính số phần tử của không gian mẫu của phép thử đó.

(3) Lập tỉ số giữa số kết quả thuận lợi của biến cố và số phần tử của không gian mẫu của phép thử.

(4) Mô tả các kết quả thuận lợi của biến cố , từ đó xác định số kết quả thuận lợi cho biến cố

Trong các hành động sau, hành động nào không phải là phép thử ngẫu nhiên?

Gieo một con xúc xắc cân đối, đồng chất và quan sát số chấm xuất hiện. Tập hợp các kết quả thuận lợi cho biến cố “Xuất hiện mặt có số chấm là số lẻ” là

Ba bạn Lan, Huệ, Nam đều chọn ngẫu nhiên ngày thứ Bảy hoặc ngày Chủ nhật tuần này, đi xem phim. Xác suất của biến cố “Ba bạn đi xem phim cùng một ngày” là

Tâm đường tròn nội tiếp của một tam giác đều không phải là giao điểm của

Cho tam giác đều cạnh thì có bán kính đường tròn ngoại tiếp là

Cho tứ giác là tứ giác nội tiếp. Khẳng định nào sau đây là đúng?

Mỗi góc trong của lục giác đều có số đo bằng

Cho hình vuông có tâm Có bao nhiêu phép quay thuận chiều tâm biến hình vuông thành chính nó?

Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)

Cho bảng tần số về điểm số của nội dung thể dục chạy 100 m mà các bạn lớp 9C đạt được như sau:

a) Cỡ mẫu của mẫu dữ liệu trên là 36.

b) Có 2 bạn học sinh đạt được điểm 9.

c) Tần số tương đối của giá trị 6 là

d) Ước lượng xác suất để chọn được một học sinh dưới 8 điểm trong lớp 9C là

Cho tứ giác có

a) Tứ giác nội tiếp đường tròn đường kính

b) Đường tròn đường kính là đường tròn nội tiếp tam giác

c) Nếu thì

d) Bán kính đường tròn ngoại tiếp tam giác bằng

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)   

Khi vẽ biểu đồ tần số tương đối dạng hình quạt tròn thì số đo cung của hình quạt tròn dùng để biểu thị tần số tương đối là bao nhiêu độ?

Một sân bóng đá có 4 cửa Hai bạn Nam và Phong cùng lúc chọn ngẫu nhiên một cửa để vào sân. Tính xác suất của biến cố : “Cả hai bạn không đi vào cửa ” (kết quả làm tròn đến chữ số thập phân thứ hai).

Cho tứ giác nội tiếp đường tròn biết Số đo cung là bao nhiêu độ?

Trong mặt phẳng tọa độ cho điểm và Hỏi phép quay ngược chiều tâm biến điểm thành điểm có góc quay bằng bao nhiêu độ?

Một ngân hàng thống kê số tiền (đơn vị: triệu đồng) mà 80 hộ gia đình vay để phát triển sản xuất. Số liệu được ghi lại trong biểu đồ tần số ghép nhóm sau:

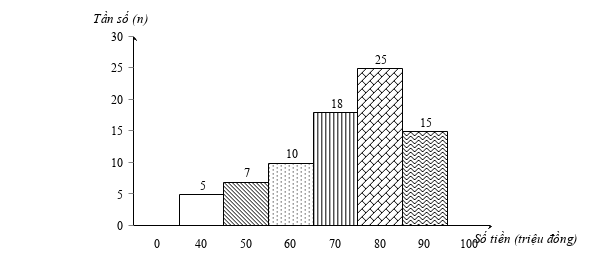
Vẽ biểu đồ tương đối ghép nhóm ở dạng biểu đồ cột của mẫu số liệu ghép nhóm đó.

Trên mặt phẳng  cho hình chữ nhật  sao cho  Gọi là tập hợp tất cả các điểm  với  là các số nguyên và nằm bên trong (không kể trên cạnh) của hình chữ nhật  Lấy ngẫu nhiên một điểm của tập hợp  Tính xác suất của biến cố  “Điểm  của tập hợp được lấy ra có x + y < 4

Cho đường tròn tâm đường kính Hai dây cung và cắt nhau tại   nằm bên trong đường tròn Vẽ vuông góc với tại Chứng minh rằng:

Tứ giác nội tiếp.

Cho đường tròn tâm đường kính Hai dây cung và cắt nhau tại   nằm bên trong đường tròn Vẽ vuông góc với tại Chứng minh rằng:Điểm là tâm đường tròn nội tiếp tam giác