Bộ 10 đề thi giữa kì 2 Toán 12 Kết nối tri thức cấu trúc mới có đáp án - Đề 03
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
![]() bằng
bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số![]() liên tục trên
liên tục trên ![]() và
và![]() thỏa mãn
thỏa mãn ![]() . Tìm mệnh đề đúng.
. Tìm mệnh đề đúng.
A.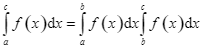 .
.
B.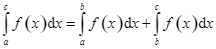 .
.
C. 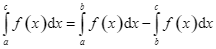 .
.
D. 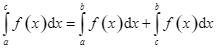 .
.
Cho hàm số ![]() liên tục trên
liên tục trên ![]() . Gọi
. Gọi ![]() là một nguyên hàm của
là một nguyên hàm của ![]() trên
trên ![]() thỏa mãn
thỏa mãn ![]() . Khi đó
. Khi đó 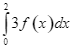 bằng
bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Diện tích của hình thang cong giới hạn bởi đồ thị hàm số ![]() , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng ![]() được tính theo công thức
được tính theo công thức
A. ![]() .
.
B. ![]() .
.
C. 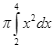 .
.
D. 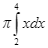 .
.
Tính 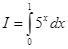
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Tính tích phân 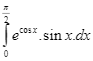 bằng
bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , mặt phẳng
, mặt phẳng ![]() có một vectơ pháp tuyến là
có một vectơ pháp tuyến là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , cho hai mặt phẳng
, cho hai mặt phẳng ![]() và
và ![]() (
(![]() là tham số). Tìm
là tham số). Tìm ![]() để
để ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian với hệ trục tọa độ ![]() , cho mặt phẳng
, cho mặt phẳng ![]() có phương trình
có phương trình ![]() và điểm
và điểm ![]() . Tính khoảng cách
. Tính khoảng cách ![]() từ
từ ![]() đến
đến ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , cho ba điểm
, cho ba điểm ![]() . Tọa độ nào sau đây là tọa độ vectơ pháp tuyến của mặt phẳng
. Tọa độ nào sau đây là tọa độ vectơ pháp tuyến của mặt phẳng ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , cho hai điểm
, cho hai điểm ![]() . Phương trình mặt phẳng trung trực của đoạn AB có một vectơ pháp tuyến là
. Phương trình mặt phẳng trung trực của đoạn AB có một vectơ pháp tuyến là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian hệ trục tọa độ ![]() , cho
, cho ![]() và mặt phẳng
và mặt phẳng ![]() . Viết phương trình mặt phẳng
. Viết phương trình mặt phẳng ![]() qua
qua ![]() và vuông góc với
và vuông góc với ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số ![]() .
.
a) ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() .
.
b) Một nguyên hàm của hàm số ![]() là
là ![]() .
.
c) Nguyên hàm ![]() của hàm số
của hàm số ![]() thỏa mãn điều kiện
thỏa mãn điều kiện ![]() là
là ![]() .
.
d) ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() , họ tất cả các nguyên hàm của hàm số
, họ tất cả các nguyên hàm của hàm số ![]() là
là ![]() .
.
Cho hàm số ![]() liên tục trên
liên tục trên ![]() .
.
a) Nếu 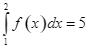 và
và 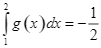 thì
thì 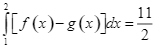 .
.
b) Nếu 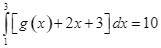 thì
thì 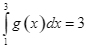 .
.
c) Nếu ![]() thì
thì ![]() .
.
d) Nếu ![]() thì
thì 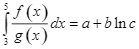 . Khi đó
. Khi đó ![]() .
.
Cho hàm số ![]() liên tục trên
liên tục trên ![]() có đồ thị như hình vẽ. Biết rằng
có đồ thị như hình vẽ. Biết rằng ![]() tạo với trục hoành và 2 đường thẳng
tạo với trục hoành và 2 đường thẳng ![]() một hình phẳng
một hình phẳng ![]() gồm 2 phần có diện tích lần lượt là
gồm 2 phần có diện tích lần lượt là ![]() .
.
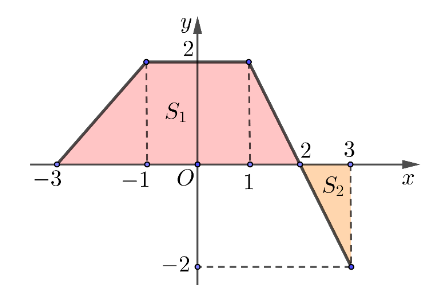
a) 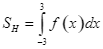 .
.
b) 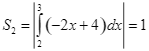 .
.
c) 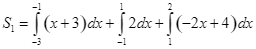 .
.
d) 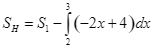 .
.
Trong không gian với hệ trục tọa độ ![]() , cho mặt phẳng
, cho mặt phẳng ![]() , mặt phẳng
, mặt phẳng ![]() song song với mặt phẳng
song song với mặt phẳng ![]() đồng thời
đồng thời ![]() cách điểm
cách điểm ![]() một khoảng bằng 3 có dạng
một khoảng bằng 3 có dạng ![]() .
.
a) Mặt phẳng ![]() đi qua gốc tọa độ.
đi qua gốc tọa độ.
b) Mặt phẳng ![]() có một vectơ pháp tuyến là
có một vectơ pháp tuyến là ![]() .
.
c) ![]() không đi qua điểm
không đi qua điểm ![]() .
.
d) Giá trị biểu thức ![]() là một số tự nhiên chia hết cho 8.
là một số tự nhiên chia hết cho 8.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.
Cho 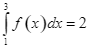 . Tính
. Tính 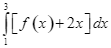 .
.
Cho ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() . Tính giá trị của
. Tính giá trị của ![]() .
.
Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 m so với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật ![]() , trong đó
, trong đó ![]() (phút) là thời gian tính từ lúc bắt đầu chuyển động,
(phút) là thời gian tính từ lúc bắt đầu chuyển động, ![]() được tính theo đơn vị mét/phút (m/p). Nếu như vậy thì khi bắt đầu tiếp đất vận tốc của khí cầu bằng bao nhiêu m/p?
được tính theo đơn vị mét/phút (m/p). Nếu như vậy thì khi bắt đầu tiếp đất vận tốc của khí cầu bằng bao nhiêu m/p?
Cho một mô hình 3D mô phỏng một đường hầm như hình vẽ bên.
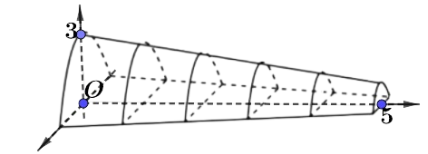
Chiều dài của đường hầm mô hình là 5 cm, mặt phẳng vuông góc với mặt đáy của đường hầm tạo được thiết diện là một hình parabol, thiết diện có độ dài cạnh đáy gấp đôi chiều cao. Tính thể tích không gian bên trong đường hầm mô hình, biết chiều cao của mỗi thiết diện parabol cho bởi công thức ![]() (đơn vị là cm), với
(đơn vị là cm), với ![]() là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình. Kết quả làm tròn đến hàng đơn vị.
là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình. Kết quả làm tròn đến hàng đơn vị.
Trong không gian ![]() , mặt phẳng
, mặt phẳng ![]() đi qua điểm
đi qua điểm ![]() và cắt trục tọa độ tại
và cắt trục tọa độ tại ![]() (khác gốc tọa độ) sao cho
(khác gốc tọa độ) sao cho ![]() là trọng tâm tam giác
là trọng tâm tam giác ![]() có phương trình là
có phương trình là ![]() . Giá trị của
. Giá trị của ![]() bằng bao nhiêu?
bằng bao nhiêu?
Mặt phẳng ![]() đi qua điểm
đi qua điểm ![]() cắt các tia
cắt các tia ![]() lần lượt tại
lần lượt tại ![]() sao cho thể tích khối tứ diện
sao cho thể tích khối tứ diện ![]() nhỏ nhất. Khi đó
nhỏ nhất. Khi đó ![]() bằng bao nhiêu?
bằng bao nhiêu?








