Bộ 5 đề thi cuối kì 2 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Đề 04
21 câu hỏi
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Nếu 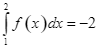 thì
thì 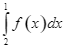 bằng
bằng
−2.
2.
0.
1.
Cho hàm số ![]() liên tục trên
liên tục trên ![]() . Biết hàm số
. Biết hàm số ![]() là một nguyên hàm của
là một nguyên hàm của ![]() trên
trên ![]() và
và ![]() . Tích phân
. Tích phân 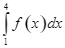 bằng
bằng
−1.
1.
3.
5.
Cho hàm số ![]() liên tục, không âm trên đoạn
liên tục, không âm trên đoạn ![]() . Gọi
. Gọi ![]() là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số ![]() , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng 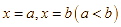 . Thể tích của khối tròn xoay tạo thành khi quay
. Thể tích của khối tròn xoay tạo thành khi quay ![]() quanh trục hoành được tính theo công thức
quanh trục hoành được tính theo công thức
A. 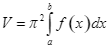 .
.
B. 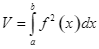 .
.
C. 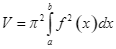 .
.
D. 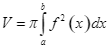 .
.
Gọi ![]() là diện tích hình phẳng giới hạn bởi các đường
là diện tích hình phẳng giới hạn bởi các đường ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
A. 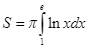 .
.
B. 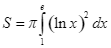 .
.
C. 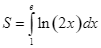 .
.
D. 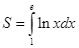 .
.
Trong không gian ![]() , cho mặt phẳng
, cho mặt phẳng ![]() . Vectơ nào dưới đây là một vectơ pháp tuyến của
. Vectơ nào dưới đây là một vectơ pháp tuyến của ![]() ?
?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng
, vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng ![]() ?
?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , cho đường thẳng
, cho đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và nhận vectơ
và nhận vectơ ![]() làm vectơ chỉ phương. Hệ phương trình nào sau đây là phương trình tham số của
làm vectơ chỉ phương. Hệ phương trình nào sau đây là phương trình tham số của ![]() ?
?
A. 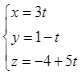 .
.
B. 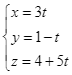 .
.
C. 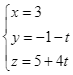 .
.
D.  .
.
Cho hai biến cố ![]() và
và ![]() . Xác suất của biến cố
. Xác suất của biến cố ![]() , tính trong điều kiện biết rằng biến cố
, tính trong điều kiện biết rằng biến cố ![]() đã xảy ra, được gọi là xác suất của
đã xảy ra, được gọi là xác suất của ![]() với điều kiện
với điều kiện ![]() kí hiệu là
kí hiệu là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , cho hai điểm
, cho hai điểm ![]() và
và ![]() . Đường thẳng
. Đường thẳng ![]() có phương trình là:
có phương trình là:
A. 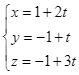 .
.
B. 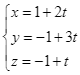 .
.
C. 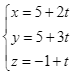 .
.
D.  .
.
Trong không gian với hệ tọa độ ![]() cho đường thẳng
cho đường thẳng 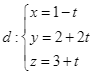 và mặt phẳng
và mặt phẳng ![]() . Tính số đo góc giữa đường thẳng
. Tính số đo góc giữa đường thẳng ![]() và mặt phẳng
và mặt phẳng ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong không gian ![]() , cho hai điểm
, cho hai điểm ![]() . Phương trình của mặt cầu đường kính
. Phương trình của mặt cầu đường kính ![]() là:
là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
![]()
Cho hai biến cố ![]() và
và ![]() với
với ![]() . Khi đó
. Khi đó ![]() bằng
bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số ![]() và
và ![]() .
.
a) ![]() .
.
b) ![]() là một nguyên hàm của
là một nguyên hàm của ![]() .
.
c) ![]() .
.
d) Biết ![]() .
.
Trong không gian ![]() , cho mặt cầu
, cho mặt cầu ![]() . Phương trình mặt phẳng
. Phương trình mặt phẳng ![]() chứa trục
chứa trục ![]() và cắt
và cắt ![]() theo giao tuyến là một đường tròn có bán kính bằng 2.
theo giao tuyến là một đường tròn có bán kính bằng 2.
a) Mặt cầu ![]() có tâm
có tâm ![]() và bán kính
và bán kính ![]() .
.
b) Gốc tọa độ ![]() nằm trong mặt cầu
nằm trong mặt cầu ![]() .
.
c) Khoảng cách từ tâm mặt cầu đến mặt phẳng ![]() bằng 1.
bằng 1.
d) Mặt phẳng ![]() có phương trình là
có phương trình là ![]() .
.
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 1 đến câu 4.
Trong không gian ![]() , có bao nhiêu giá trị nguyên dương
, có bao nhiêu giá trị nguyên dương ![]() để phương trình
để phương trình ![]() là phương trình mặt cầu?
là phương trình mặt cầu?
Gieo lần lượt hai con xúc xắc cân đối và đồng chất. Cho hai biến cố ![]() : “Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn 6” và
: “Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn 6” và ![]() “Con xúc xắc thứ nhất xuất hiện mặt 4 chấm”. Có bao nhiêu kết quả thuận lợi cho biến cố
“Con xúc xắc thứ nhất xuất hiện mặt 4 chấm”. Có bao nhiêu kết quả thuận lợi cho biến cố ![]() khi biến cố
khi biến cố ![]() xảy ra?
xảy ra?
Hộp thứ nhất chứa 3 viên bi đen và 2 viên bi trắng. Hộp thứ hai chứa 4 viên bi đen và 5 viên bi trắng. Các viên bi có cùng kích thước và khối lượng. Bạn An lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất bỏ vào hộp thứ hai, sau đó lại lấy ra ngẫu nhiên 1 viên bi từ hộp thứ hai.
Gọi A: “Viên bi lấy ra lần thứ nhất là bi đen”;
Và B: “Viên bi lấy ra lần thứ hai là bi trắng”.
Biết rằng biến cố A xảy ra, tính xác suất của biến cố B.
Trong một đợt kiểm tra sức khỏe, có một loại bệnh X mà tỉ lệ người mắc bệnh là 0,2% và một loại xét nghiệm Y mà ai mắc bệnh X khi xét nghiệm Y cũng có phản ứng dương tính. Tuy nhiên, có 6% những người không bị bệnh X lại có phản ứng dương tính với xét nghiệm Y. Chọn ngẫu nhiên 1 người trong đợt kiểm tra sức khỏe đó. Giả sử người đó có phản ứng dương tính với xét nghiệm Y. Tính xác suất người đó bị mắc bệnh X (làm tròn kết quả đến hàng phần trăm).
PHẦN II. TỰ LUẬN
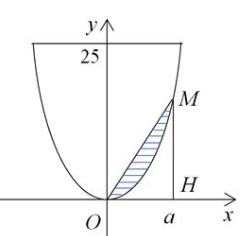
Ông B có một khu vườn giới hạn bởi một đường parabol và một đường thẳng. Nếu đặt trong hệ tọa độ ![]() như hình vẽ dưới đây thì parabol có phương trình
như hình vẽ dưới đây thì parabol có phương trình ![]() và đường thẳng
và đường thẳng ![]() . Ông B dự định dùng mảnh vườn nhỏ được chia từ khu vườn bởi một đường thẳng đi qua O và điểm M trên parabol để trồng hoa. Hãy giúp ông B xác định điểm M bằng cách tính độ dài OM để diện tích mảnh vườn nhỏ bằng
. Ông B dự định dùng mảnh vườn nhỏ được chia từ khu vườn bởi một đường thẳng đi qua O và điểm M trên parabol để trồng hoa. Hãy giúp ông B xác định điểm M bằng cách tính độ dài OM để diện tích mảnh vườn nhỏ bằng ![]() .
.
Trong không gian ![]() , cho điểm
, cho điểm ![]() , mặt phẳng
, mặt phẳng ![]() và mặt cầu
và mặt cầu ![]() . Gọi
. Gọi ![]() là đường thẳng đi qua
là đường thẳng đi qua ![]() , nằm trong
, nằm trong ![]() và cắt
và cắt ![]() tại hai điểm có khoảng cách nhỏ nhất. Viết phương trình đường thẳng
tại hai điểm có khoảng cách nhỏ nhất. Viết phương trình đường thẳng ![]() .
.
Cho hai biến cố ![]() và
và ![]() với
với ![]() .
.
a) Tính ![]() .
.
b) Tính ![]() .
.








