Bài tập Hình học không gian OXYZ cơ bản, nâng cao có lời giải (P9)

Trong không gian Oxyz, cho điểm A(-1;3;-2) và mặt phẳng $\left(\alpha \right)$: x-2y-2z+5=0.Khoảng cách từ điểm A đến mặt phẳng $\left(\alpha \right)$bằng:

Trong không gian  Oxyz, cho điểm A(2;-1;1). Phương trình mặt phẳng $\left(\alpha \right)$ đi qua hình chiếu của điểm A trên các trục tọa độ là

Trong không gian Oxyz, cho 2 mặt phẳng (P): x+2y-2z+2018=0, (Q): x+my+(m-1)z+2017=0 (m là tham số thực). Khi hai mặt phẳng (P) và (Q) tạo với nhau một góc nhỏ nhất thì điểm M nào dưới đây nằm trong (Q) ?

Trong  không  gian  Oxyz,  cho  các  điểm A(1;-1;1), B(-1;2;3) và đường  thẳng $d_{}: \frac{x+1}{-2}=\frac{y-2}{1}=\frac{z-3}{3}$. Đường thẳng $∆$ đi qua điểm A, vuông góc với hai đường thẳng AB và d có phương trình là:

Trong không gian Oxyz, cho điểm M(1;2;3). Hỏi có bao nhiêu mặt phẳng (P) đi qua M  và cắt trục x'Ox, y'Oy, z'Oz lần lượt tại các điểm A, B, C sao cho OA=2OB=3OC>0.

Trong không gian  Oxyz,  cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với  a, b, c  là những số thực dương thay đổi sao cho $a^2+4b^2+16c^2=49$. Tính tổng $F=a^2+b^2+c^2$  sao cho khoảng cách từ  O đến (ABC) là lớn nhất.

Trong không gian với hệ  tọa độ  Oxyz, tính thể  tích tứ  diện OABC biết A, B, C lần lượt là giao điểm của mặt phẳng 2x-3y+4z+24=0 với các trục Ox, Oy, Oz.

Trong không gian với hệ tọa độ Oxyz, cho điểm  M(1;-1;2), N(3;1;-4). Viết phương trình mặt phẳng trung trực của MN?

Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;1;1) và hai mặt phẳng (P):2x-y+3z-1=0, (Q): y=0. Viết phương trình mặt phẳng chứa A, vuông góc với cả  hai mặt phẳng và ?

Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) chứa  điểm M(1;3;-2), cắt các tia Ox, Oy, Oz  lần lượt tại các điểm A, B, C sao cho  $\frac{OA}{1}=\frac{OB}{2}=\frac{OC}{4}$

Trong không gian với  hệ tọa độ Oxyz, viết phương trình mặt phẳng tiếp xúc với $\left(S\right): x^2+y^2+z^2-2x-4y-6z-2=0$ và song song với $\left(\alpha \right)$: 4x+3y-12z+10=0

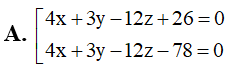
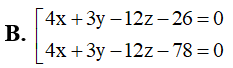
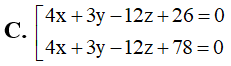
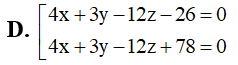
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(-1;-2;0), B(0;-4;0), C(0;0;-3). Phương trình mặt phẳng (P) nào dưới đây đi qua A, gốc tọa độ O và cách đều hai điểm B và C?

Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(-2;4;1), B(1;1;-6), C(0;-2;3). Tìm tọa độ trọng tâm G của tam giác ABC.

Trong không gian với hệ tọa độ  Oxyz, mặt phẳng (P):2x+3y+4z-12=0 cắt trục Oy tại điểm có tọa độ là

Trong không gian với hệ tọa độ Oxyz, mặt phẳng đi qua điểm A(2;-3;-2) và có một vectơ pháp tuyến $\overrightarrow{n}=(2;-5;1)$ có phương trình là

Trong không gian với hệ tọa độ Oxyz, cho điểm I(1;2;-5) và mặt phẳng (P): 2x-2y+z-8=0. Viết phương trình mặt cầu có tâm I và tiếp xúc với mặt phẳng  (P)

Trong không gian Oxyz, cho hai điểm A(2;4;1), B(-1;1;3) và mặt phẳng (P): x-3y+2z-5=0. Viết phương trình mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng  (P).

Trong không gian với hệ trục tọa độ vuông góc Oxyz, cho mặt phẳng (P): 2x+y+6z-1=0 và hai điểm A(1;-1;0), B(-1;0;1). Hình chiếu vuông góc của đoạn thẳng AB trên mặt phẳng (P) có độ dài bao nhiêu?

Trong  không  gian  Oxyz,  cho  hai  mặt  phẳng (P): 2x-y+3z-1=0 và mặt  phẳng (Q): 4x-2y+6z-1=0. Trong các mệnh đề sau, mệnh đề nào đúng?

Trong không gian Oxyz, cho điểm M(1;0;3) thuộc:

Trong không gian  Oxyz, cho đường thẳng  d  đi qua M(2;0;-1) và có VTCP là $\overrightarrow{u}$ =(2;-3;1). Phương trình chính tắc của đường thẳng d là:

Trong không gian Oxyz, cho tam giác  ABC  với A(-1;0;2), B(1;2;-1), C(-3;1;2). Mặt phẳng (P)  đi qua trọng tâm của tam giác ABC và vuông góc với đường thẳng AB là:

Trong không gian Oxyz, cho hai đường thẳng $d_1:\frac{x-1}{2}=\frac{y}{-1}=\frac{z+2}{1}$ và $d_2:\frac{x+1}{1}=\frac{y-1}{7}=\frac{z-3}{-1}$. Đường vuông góc chung của $d_1$ và  $d_2$ lần lượt cắt , tại A và B. Diện tích tam giác OAB bằng

Trong không gian Oxyz, cho đường thẳng $d_{}:\frac{x-2}{1}=\frac{y-1}{-2}=\frac{z-1}{2}$ và hai điểm A(3;2;1), B(2;0;4). Gọi là $∆$ đường thẳng qua A, vuông góc với d sao cho khoảng cách từ  B đến $∆$ là  nhỏ nhất.  Gọi $\overrightarrow{u}$ =(2;b;c)  là một VTCP của $∆$. Khi đó, $\left|\overrightarrow{u}\right|$bằng

Trong không gian Oxyz, cho mặt cầu $\left(S\right): x^2+y^2+z^2-6x+4y-2z+5=0$ Phương  trình  mặt phẳng (Q) chứa trục Ox và cắt (S) theo giao tuyến là một đường tròn bán kính bằng 2 là

Cho ba tia Ox, Oy, Oz  đôi một vuông góc với nhau. Gọi C là điểm cố  định trên  Oz, đặt OC=1 các điểm A, B thay đổi trên Ox, Oy sao cho OA+OB=OC. Giá trị bé nhất của bán kính mặt cầu ngoại tiếp tứ diện OABC là

Trong không gian Oxyz, cho mặt phẳng  Mặt phẳng (P): x-2y+3z-1=0 có một vectơ pháp tuyến là

Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(3;0;0), N(0;-2;0) và P(0;0;2). Mặt phẳng (MNP) có phương trình là

Trong không gian với hệ tọa độ Oxyz cho mặt cầu $\left(S\right): {\left(x-5\right)}^2+{\left(y-1\right)}^2+{\left(z+2\right)}^2=16$  Tính bán kính của (S)