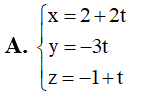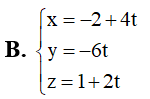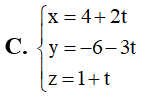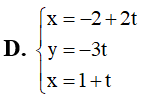Bài tập Hình học không gian OXYZ cơ bản, nâng cao có lời giải (P3)

Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A(2;-3;7), B(0;4;1), C(3;0;5), D(3;3;3).  Gọi M là điểm nằm trên mặt phẳng (Oyz) sao cho biểu thức $\left|\overrightarrow{MA }+ \overrightarrow{MB} + \overrightarrow{MC} + \overrightarrow{MD}\right|$ đạt giá trị nhỏ nhất. Khi đó tọa độ M là

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;0;0), B(0;2;0), C(0;0;3). Tập hợp các điểm M thỏa $M{A}^2=M{B}^2+M{C}^2$ là mặt cầu có bán kính

Trong không gian tọa độ Oxyz cho ba điểm A(2;5;1), B(-2;-6;2), C(1;2;-1) và điểm M(m;m;m) để $\left|\overrightarrow{MB}-2\overrightarrow{AC}\right|$ đạt giá trị nhỏ nhất thì m bằng

Trong không gian Oxyz, cho 2 điểm B(1;2;-3), C(7;4;-2). Nếu E là điểm thỏa mãn đẳng thức $\overrightarrow{CE} =2\overrightarrow{EB}$  thì tọa độ điểm E là

Ba đỉnh của một hình bình hành có tọa độ là (1;1;1), (2;3;4), (7;7;5). Diện tích của hình bình hành đó bằng

Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(3;-2;-2), B(3;2;0), C(0;2;1). Phương trình mặt phẳng (ABC) là:

Trong không gian Oxyz, đường thẳng d: $\frac{x-1}{3}=\frac{y+2}{-4}=\frac{z-3}{-5}$ đi qua điểm

Trong không gian Oxyz, cho điểm A(4;2;1) và B(2;0;5). Tọa độ vecto $\overrightarrow{AB}$ là:

Trong không gian Oxyz, mặt phẳng (P): x+2y-3z +3 =0 có một vecto pháp tuyến là:

Trong không gian Oxyz, cho mặt phẳng (P): 2x - 2y+z +5=0. Khoảng cách từ điểm M(-1;2;-3) đến mp (P) bằng:

Trong không gian Oxyz ,cho ba điểm A(1;1;1), B(-1;2;0), C(2;-3;2). Tập hợp tất cả các điểm M cách đều ba điểm A, B, C là một đường thẳng d. Phương trình tham số của d là

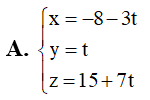
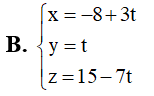
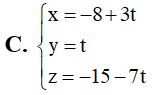
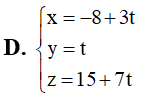
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-1;2;1), B(1;2;-3) và đường thẳng d: $\frac{x+1}{2}=\frac{y-5}{2}=\frac{z}{-1}$ Tìm vectơ chỉ phương  của đường thẳng  đi qua A và vuông góc với d đồ ng thời cách  B  một khoảng lớn nhất.

Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;0;-1) và mặt phẳng (P): x+ y -z -3 =0. Mặt cầu (S) có tâm I nằm trên mặt phẳng  (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 +$\sqrt{2}$. Phương trình mặt cầu  (S) là

Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(0;1;3), N(10;6;0) và mặt phẳng (P): x - 2y+ 2z -10=0. Điểm I(-10;a;b)  thuộc mặt phẳng (P) sao cho  $\left|IM -IN\right|$ lớn nhất. Khi đó tổng T = a+b   bằng

Cho mặt phẳng $\left(\alpha \right): 2x -3y-4z+1=0$. Khi đó, một véc- tơ pháp tuyến của  $\left(\alpha \right)$

Cho hai mặt phẳng $\left(\alpha \right): 3x-2y+2z+7=0$, $\left(\beta \right): 5x-4y+3z+1=0$. Phương trình mặt phẳng đi qua gốc tọa độ O đồng thời vuông góc với cả $\left(\alpha \right)$ và $\left(\beta \right)$ là:

Cho tam giác ABC với A(2;-3;2), B(1;-2;2), C(1;-3;3). Gọi A’, B’, C’ lần lượt là hình chiếu vuông góc của A, B, C lên mặt phẳng $\left(\alpha \right): 2x-y+2z-3=0$   Khi đó, diện tích tam giác A’B’C’ bằng

Trong không gian với hệ tọa độ Oxyz, cho A(1;2;-3), $B(\frac{3}{2};\frac{3}{2};-\frac{1}{2})$,C(1;1;4), D(5;3;0). Gọi $\left(S_1\right)$ là mặt cầu tâm A bán kính bằng 3, $\left(S_2\right)$ là mặt cầu tâm B bán kính bằng $\frac{3}{2}$ Có bao nhiêu mặt phẳng tiếp xúc với 2 mặt cầu $\left(S_1\right)$,$\left(S_2\right)$ đồng thời song song với đường thẳng đi qua 2 điểm C D.

Trong không gian Oxyz, mặt phẳng (P): 2x - y + 3z - 1 =0 có một vectơ pháp tuyến là:

Trong không gian Oxyz , cho ba điểm M(2;0;0), N(0;1;0) và P(0;0;2). Mặt phẳng (MNP) có phương trình là

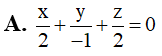
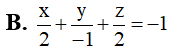
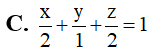
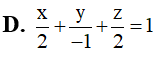
Trong không gian Oxyz, cho điểm M(3;2;-1). Hình chiếu vuông góc của điểm M lên trục Oz là điểm:

Trong không gian với hệ toạ độ Oxyz, cho ba điểm  A(2;-1;1), B(1;0;4) và C(0;-2;-1). Phương trình mặt phẳng qua A và vuông góc với đường thẳng BC là:

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(2;-3;7), B(0;4;-3), C(4;2;5). Biết điểm $M(x_0;y_0;z_0)$ nằm trên mp (Oxy) sao cho $\left|\overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC}\right|$ có giá trị nhỏ nhất. Tổng $P=x_0 +y_0+z_0$ có giá trị bằng

Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(2;2;1), $B\left(-\frac{8}{3};\frac{4}{3};\frac{8}{3}\right)$. Biết I(a;b;c) là tâm đường tròn nội tiếp của tam giác OAB. Tính tổng  S =a + b + c

Trong không gian với hệ trục tọa độ Oxyz, cho A(0;-1;1),B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là:

Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua hai điểm A(2;1;3), B(1;-2;1) và song song với đường thẳng d $\left\{\begin{array}{l}x=-1+t\\ y=2t\\ z=-3-2t\end{array}\right.$

Trong không gian Oxyz, mặt cầu tâm I(1;2;3) đi qua điểm A(1;1;2) có pt là:

Lập phương trình của mặt phẳng đi qua A(2;6;-3) và song song với (Oyz).

Cho đường thẳng $∆$  đi qua điểm M(2;0;-1) và có vectơ chỉ phương $\overrightarrow{a}=(4;-6; 2)$. Phương trình tham số của đường thẳng $∆$ là: