30 câu hỏi
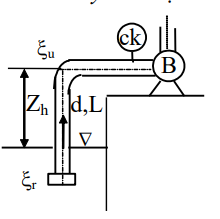
Biết độ cao chân không tại mặt cắt vào bơm hck = 4,5 m cột nước; ống hút có d = 150 mm; L = 10 m; hệ số ma sát λ = 0,03; hệ số tổn thất tại lưới chắn rác ξᵣ = 6,0; chỗ uốn ξᵤ = 0,2; lưu lượng qua bơm Q = 16 dm³/s. Nước chảy rối. Độ cao đặt bơm zₕ bằng:
3,5 m
5,5 m
4,3 m
4,1 m
Một bơm nước có N = 60 kW, η = 80%, làm việc với Q = 0,15 m³/s và độ cao chân không cho phép [Hck] = 6 m. Tổng tổn thất cục bộ trên đường ống hút ∑hₐₜₕ = 5 m, bỏ qua tổn thất dọc đường, d₁ = d₂ = 250 mm. Nước chảy rối. Chiều cao hút cho phép [zₕ] của bơm bằng:
![Một bơm nước có N = 60 kW, η = 80%, làm việc với Q = 0,15 m³/s và độ cao chân không cho phép [Hck] = 6 m. Tổng tổn thất cục bộ trên đường ống hút ∑hₐₜₕ = 5 m, bỏ qua tổn thất dọc đường, d₁ = (ảnh 1)](https://video.vietjack.com/upload2/images/1752750725/1752750787-image2.png)
6,5 m
6,8 m
3,2 m
3,5 m
Với cùng cột áp H và tiết diện S, lưu lượng của chất lỏng chảy tự do qua vòi có chiều dài l=(3÷4)dl = (3 \div 4)dl=(3÷4)d so với lưu lượng qua lỗ:
Lớn hơn
Nhỏ hơn
Bằng
Chưa đủ điều kiện để so sánh
Trong công thức tính lưu lượng dòng chảy tự do qua lỗ từ một bể hở:Q=μS\(\sqrt {2gH} \), H là:
Chênh lệch độ cao giữa mặt thoáng và đáy bình.
Chênh lệch độ cao giữa mặt thoáng và tâm lỗ
Chênh lệch độ cao của mặt thoáng tại các thời điểm khác nhau
Chưa có đáp án chính xác
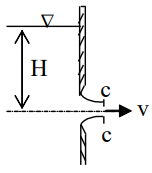
Xét dòng chảy qua lỗ tháo, v là vận tốc dòng chảy khi ra khỏi lỗ tại mặt cắt co hẹp. Ta có:
Luôn luôn v<\(\sqrt {2gH} \)
Luôn luôn v>\(\sqrt {2gH} \)
Luôn luôn v=\(\sqrt {2gH} \)
Chưa có đáp án chính xác
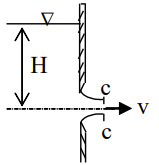
Dòng chảy qua lỗ mỏng như hình vẽ, v là vận tốc dòng chảy ra khỏi lỗ tại mặt cắt co hẹp, S là tiết diện lỗ, Sc là tiết diện dòng chảy tại mặt cắt co hẹp, φ là hệ số vận tốc và μ là hệ số lưu lượng. Ta có:
Q=φ⋅S⋅v
Q=μ⋅Sc⋅v
Q=S⋅v
Q=Sc⋅v
Hệ số lưu lượng của dòng chảy qua vòi:
Luôn luôn nhỏ hơn 1 vì co hẹp dòng
Luôn luôn nhỏ hơn 1 vì tổn thất dọc đường
Có thể lớn hơn hoặc nhỏ hơn 1
Luôn luôn nhỏ hơn 1 vì co hẹp dòng và tổn thất năng lượng
Hệ số lưu lượng μ trong công thức tính lưu lượng qua lỗ sẽ nhỏ khi:
Tổn thất cục bộ qua lỗ nhỏ
Không có tổn thất năng lượng
Dòng chảy qua lỗ bị co hẹp nhiều
Chưa có đáp án chính xác
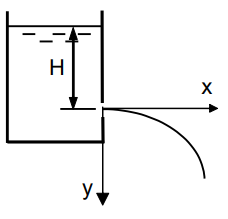
Người ta khoan một lỗ trên thành bể có cột nước bằng H để tháo nước. Bỏ qua ma sát. Với hệ trục gắn như hình vẽ thì phương trình quỹ đạo chuyển động của dòng chảy ra lỗ là:
y=Hx2
y=2gHx2
y=\(\frac{{{x^2}}}{{2gH}}\)
y=\(\frac{{{x^2}}}{{4H}}\)
Một bể chứa dài 10 m, rộng 5 m, chứa chất lỏng cao h = 2 m. Bỏ qua tổn thất. Thời gian tháo cạn bể qua lỗ có diện tích S = 0,5 dm² lắp dưới đáy bể bằng (giây):
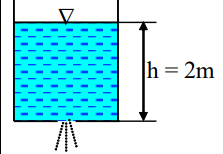
3193
6385
7385
9577
Khái niệm đường ống dài trong tính toán thủy lực đường ống là loại đường ống:
Chiều dài L >> đường kính d của ống
Độ nhám Δ << đường kính d
</<>
Cả 3 câu kia đều sai
Tổn thất dọc đường rất lớn so với tổn thất cục bộ
Khi tính toán thủy lực hệ thống đường ống phân nhánh hở:
Cột áp các nhánh được cộng lại để tính cột áp của hệ thống
Tổn thất năng lượng trong các nhánh bằng nhau
Việc xác định nhánh cơ bản là cần thiết
Lưu lượng trong các nhánh bằng nhau
Khi tính toán thủy lực đường ống phân nhánh hở, nhánh cơ bản là nhánh:
Có tổn thất năng lượng lớn nhất
Có yêu cầu về năng lượng lớn nhất
Cao nhất
Dài nhất
Khi tính toán thủy lực hệ thống đường ống nối tiếp:
Lưu lượng trong các đoạn ống bằng nhau
Tổn thất năng lượng trong các đoạn ống bằng nhau
Cột áp của hệ thống bằng cột áp của từng đoạn ống
Lưu lượng của hệ thống bằng tổng lưu lượng của các đoạn ống
Khi tính toán thủy lực hệ thống đường ống song song:
Tất cả các câu kia đều đúng
Tổn thất năng lượng trong các nhánh bằng nhau
Cột áp của hệ thống bằng cột áp của các nhánh
Lưu lượng của hệ thống bằng tổng lưu lượng của các nhánh
Hai bể chứa A, B và một hệ thống đường ống như hình vẽ. Ở cuối hệ thống lưu lượng nước cung cấp là Qr
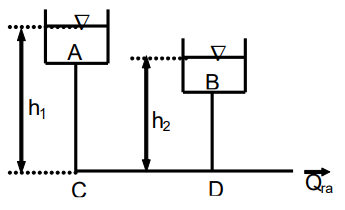
Ta có mối quan hệ về lưu lượng nước chảy trong các nhánh:
QAC = QDB + Qra
Qra = QBD + QAC
QBD = QAC + Qra
Chưa có đủ cơ sở để kết luận
Hai nhánh ống 1 và 2 có đường kính d và chiều dài L như nhau được lắp song song như hình vẽ. Ở nhánh 1 người ta lắp thêm một lưới lọc có tổn thất cục bộ ξₗ. Qi, hwi là lưu lượng và tổn thất năng lượng qua nhánh i (i = 1, 2). Ta có:
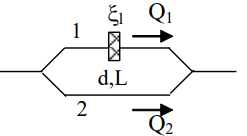
Q1 < Q2
hw1 > hw2
Q1 > Q2
hw1 < hw2</>
Dòng chảy qua mạng ống như hình vẽ. Qi, hi là lưu lượng và tổn thất năng lượng dọc đường trong nhánh thứ i. Ta có:
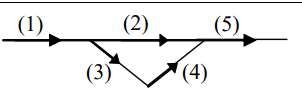
Q1 = Q2 + Q3 + Q4
hd2 = hd3
Q1 = Q5
hd2 = hd3 + hd4 - hd5
Một hệ thống đường ống rẽ nhánh có gắn một máy bơm như hình vẽ. Lưu lượng Q1, Q2, Q3 sẽ là:
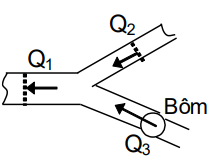
Q1 = Q2 - Q3
Q1 = Q2 = Q3
Q1 = Q2 + Q3
Q1 = Q3 - Q2
Ba bồn chứa nối với nhau như hình vẽ, mực nước trong bồn I cao hơn bồn II và mực nước bồn II cao hơn bồn III. Dòng chảy trong ống sẽ là:
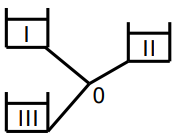
Bồn I chảy về 0, 0 chảy về bồn II
Bồn I chảy về 0, bồn II chảy về 0
Bồn II chảy về 0, 0 chảy về bồn III
Chưa đủ cơ sở để xác định
Nước chảy từ bể qua mạng lưới ống dẫn như hình vẽ, lưu lượng nước lấy ra khỏi các điểm B, C, D, E, F là q. Lưu lượng nước chảy trong ống BD là:
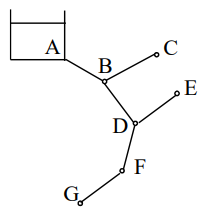
2q
5q
3q
4q
Nước chảy trong hệ thống đường ống, vận tốc v tính bằng công thức:
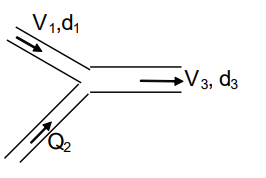
\({v_1} = {v_3}{\left( {\frac{{{d_3}}}{{{d_1}}}} \right)^2} - {Q_2}\frac{{\pi d_1^2}}{4}\)
\({v_1} = \frac{{4Q}}{{\pi d_1^2}} + {v_3}{\left( {\frac{{{d_3}}}{{{d_1}}}} \right)^2}\)
\({v_1} = {v_3}{\left( {\frac{{{d_3}}}{{{d_1}}}} \right)^2} - \frac{{4Q}}{{\pi d_1^2}}\)
\({v_1} = {Q_2} + {v_3}{\left( {\frac{{{d_3}}}{{{d_1}}}} \right)^2}\)
Trường hợp nào sau đây đủ điều kiện cho ta xác định được vận tốc trung bình của một dòng chảy có áp trong ống tròn:
Biết lưu lượng và đường kính ống
Biết trạng thái của dòng chảy và vận tốc tại tâm ống
Biết hệ số nhám của ống, đường kính ống và độ dốc thủy lực
Cả 3 trường hợp kia đều được
Ba bình hình trụ có kích thước bằng nhau và chứa chất lỏng với độ cao H như nhau (Bình 1: dầu; 2: nước; 3: thủy ngân), bỏ qua ma sát, so sánh thời gian T để tháo hết chất lỏng qua lỗ nhỏ có cùng đường kính bằng D ở dưới đáy bình, ta có:
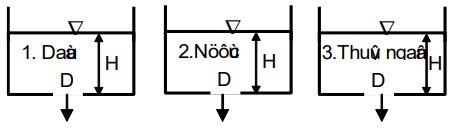
T₁ < T₂ < T₃
</>
T₁ > T₂ > T₃
T₁ = T₂ = T₃
Chưa có cơ sở để so sánh
Khi tính lưu lượng dòng chảy ổn định từ (1) qua van tiết lưu (có chiều dày δ = 0,5d) sang (2), ta có thể áp dụng công thức tính lưu lượng của bài toán:
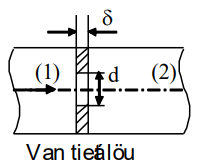
Dòng chảy tự do qua lỗ nhỏ, thành mỏng, cột áp không đổi
Dòng chảy ngập qua lỗ, thành mỏng, cột áp không đổi
Dòng chảy qua vòi trụ
Cả 3 câu kia đều sai
Các đường ống có chiều dài và đường kính khác nhau nối với nhau như hình vẽ. Gọi HA, HB là cột áp thủy tĩnh tại A và B; hWi là tổn thất cột áp trên ống thứ i. Cột áp thủy tĩnh tại B là:
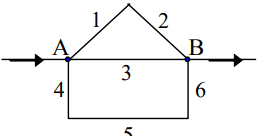
HB = HA - hW1 - hW2 - hW3 - hW4 - hW5 - hW6
HB = HA - hW1 + hW2
HB = HA - hW1 - hW2 - hW3
HB = HA - hW4 - hW5 - hW6
Điều kiện để áp dụng công thức tính cột áp H=\(\frac{{{Q^2}}}{{{K^2}}}L\) là:
1. dòng chảy tầng
2. dòng chảy đều có áp
3. dòng chảy rối
4. dòng chảy rối thành trơn thủy lực
5. dòng chảy rối thành nhám thủy lực
6. đường ống dài
1, 2, 6
3, 5, 6
2, 4, 6
2, 5, 6
Công thức H=\(\frac{{128vLQ}}{{g\pi {d^4}}}\) trong bài toán thủy lực đường ống đơn giản, có thể dùng để tính:
Tổn thất dọc đường của dòng chảy đều
Tổn thất dọc đường của dòng chảy tầng
Cột áp của dòng chảy rối
Cột áp và tổn thất dọc đường của dòng chảy tầng, đường ống dài
Công thức tính tổn thất dọc đường hd=\(\frac{{{Q^2}}}{{{K^2}}}L\) được dùng để tính cho:
Tất cả các trường hợp chảy tầng hoặc chảy rối
Chỉ cho trường hợp chảy rối thành hoàn toàn nhám
Cho tất cả các trường hợp chảy rối
Chưa có đáp án chính xác
Trong công thức tính lưu lượng Q=K\(\sqrt J \) , đơn vị của K là:
m³/s
m/s
J/N
\(\sqrt[3]{m}\)/s
