17 câu hỏi
Tìm miền giá trị của hàm số \[f\left( x \right) = \sqrt {\arctan x - \frac{\pi }{4}} \]
\[\left[ {0;\frac{{\sqrt \pi }}{2}} \right)\]
\[\left[ {0;\frac{{\sqrt \pi }}{2}} \right]\]
\[\left( {0;\frac{{\sqrt \pi }}{2}} \right)\]
\[\left( {0;\frac{\pi }{2}} \right)\]
Cho hàm số \[\left\{ {\begin{array}{*{20}{c}}{x\left( t \right) = \ln \left( {{t^3} + 2} \right) - 1}\\{y\left( t \right) = \sin \left( {{t^2} - t - 2} \right)}\end{array}} \right.\]. Đạo hàm của y theo x tại x = - 1 là:
𝑦 ′(−1) = 0.
𝑦 ′(−1) = −1.
𝑦 ′(−1) = 1.
𝑦 ′(−1) = −3.
Cực trị của hàm ẩn 𝑦 = (𝑥) cho bởi phương trình tham số 𝑥 = 2 − 𝑡; 𝑦 = 𝑡3 − 3𝑡 + 2; 𝑡 ∈ ℝ là:
Hàm số không có cực trị.
Hàm số đạt cực trị tại 𝑥 = 1; và cực tiểu tại 𝑥 = 3.
Hàm số đạt cực trị tại 𝑥 = 3; và cực tiểu tại 𝑥 = 1.
Hàm số đạt cực trị tại 𝑥 = −1; và cực tiểu tại 𝑥 = 1.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \[y = \left| {{x^3} - 3x + 2} \right|\] trên đoạn [–3; 2].
\[{y_{\max }} = 16,{y_{\min }} = 0\]
\[{y_{\max }} = 0,{y_{\min }} = 16\]
\[{y_{\max }} = 2,{y_{\min }} = - 2\sqrt 2 \]
Các câu khác sai
Một chiếc camera đặt cạnh đường 40𝑚 quan sát dõi theo một chiếc xe con di chuyển với vận tốc v = 36 km/h . Camera quay với vận tốc góc bao nhiêu khi xe con cách chỗ ngang qua với camera 70𝑚?
Đáp án khác.
0,0232.
0,0757.
0,0428.
Lực nước cản con thuyền tỷ lệ với vận tốc của nó. Vận tốc ban đầu của thuyền là 1,5 m/s, vận tốc của nó sau 4 giây là 1 m/s. Thuyền đi được một quãng đường xấp xỉ bằng bao nhiêu cho đến khi dừng lại?
12 m.
15 m.
17 m.
19 m.
Tìm biểu thức biểu diễn của hàm 𝑓 cho bởi đồ thị dưới đây?
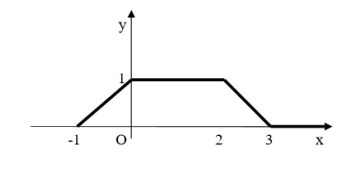
\[f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x + 1, - 1 < x < 0}\\{1,\,\,\,\,\,\,\,\,\,\,\,\,0 \le x \le 2}\\{ - x + 3,2 < x \le 3}\\{0,\,\,\,\,\,\,3 \ge x}\end{array}} \right.\]</>
\[f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x + 1, - 1 \le x \le 0}\\{1,\,\,\,\,\,\,\,\,\,\,\,\,\,0 < x \le 2}\\{ - x + 3,2 < x \le 3}\\{0,\,\,\,\,3 \le x}\end{array}} \right.\]
</>
\[f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x + 1, - 1 < x \le 0}\\{1,\,\,\,\,\,\,\,\,\,\,\,\,\,0 < x \le 2}\\{ - x - 3,2 < x \le 3}\\{0,\,\,\,\,3 \le x}\end{array}} \right.\]
Không có câu nào có đáp án đúng.
Hàm số nào sau đây không chẵn cũng không lẻ?
\[f\left( x \right) = 2 - x + 3{x^4}\]
\[g\left( x \right) = 2x - {x^5}\]
\[f\left( x \right) = 3 + 3{x^6}\]
A, B, C đều sai.
Hình vẽ sau là đồ thị của hàm số nào?
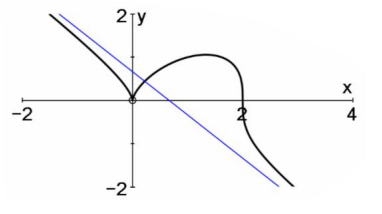
\[g\left( x \right) = \sqrt[3]{{2{x^2} + {x^3}}}\]
\[g\left( x \right) = \sqrt[3]{{ - 2{x^2} + {x^3}}}\]
\[g\left( x \right) = \sqrt[3]{{{x^2}\left( {x - 2} \right)}}\]
\[g\left( x \right) = \sqrt[3]{{2{x^2} - {x^3}}}\]
Tính giới hạn hàm số \[I = \mathop {\lim }\limits_{x \to {0^ + }} {\left( {2019x} \right)^{\frac{1}{{\ln x}}}}\]
I = 0
I = 1
\[I = \sqrt e \]
Cho hàm tham số hóa \[y\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x = {t^3} + t}\\{y = {t^2} + 2}\end{array}} \right.\]. Tính đạo hàm cấp 2 y’’(2).
\[ - \frac{1}{{16}}\]
\[\frac{1}{3}\]
2
\[\frac{1}{{12}}\]
Tìm \[ \propto \] để hàm số \[f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{{{\left( {1 - \sin 2x} \right)}^{\cot x}},x \ne 0}\\{\alpha ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 0}\end{array}} \right.\] liên tục tại x0 = 0.
α = e-2
α = e2
α = 1
α = e
Số tiệm cận của hàm số \[f\left( x \right) = \frac{x}{{\sqrt {{x^2} - 1} }}\] là
1.
4.
3.
2.
Tìm 𝑎, 𝑏 để hàm số (𝑥) = 𝑥4 − 4𝑥3 + 𝑎𝑥2 + 2𝑥 + 𝑏 có điểm uốn là (2,0).
𝑎 = 0, 𝑏 = 12.
𝑎 = 1, 𝑏 = 0.
𝑎 = −7/2, 𝑏 = 25/2.
Các câu khác sai.
Tìm 𝛼, 𝛽 để hàm số \[h\left( x \right) = \sqrt {1 - 2x} - 1 - \ln \left( {1 - x} \right) \sim \alpha {x^\beta }\] khi 𝑥 → 0.
\[\alpha = - \frac{1}{6},\beta = 3\]
\[\alpha = \frac{2}{3},\beta = 3\]
= 1, = 2.
Các câu khác sai.
Cho hàm tham số \[\left\{ {\begin{array}{*{20}{c}}{x\left( t \right) = {{\cos }^3}t.}\\{y\left( t \right) = {{\sin }^3}t.}\end{array}} \right.\]. Tính 𝑦′′(𝑥) tại \[t = \frac{\pi }{4}\] ?
\[\frac{8}{{3\sqrt 2 }}\]
\[ - \frac{2}{{3\sqrt 2 }}\]
\[\frac{4}{{3\sqrt 2 }}\]
0.
Cho (𝑥) là hàm khả vi tại mọi 𝑥 và \[g\left( x \right) = \left( {{x^2} - 2} \right)f\left( {\frac{{\cos x}}{{x + 1}}} \right)\]. Biết 𝑓 ′(1) = 3, tính 𝑔 ′(0).
𝑔 ′(0) = 6.
𝑔 ′(0) = −6.
𝑔 ′(0) = 3.
𝑔 ′(0) = −2.
