25 câu hỏi
Phương của véctơ mômen ngẫu lực..... mặt phẳng tác dụng của ngẫu lực.
Cùng chiều với
Song song với
Nằm trong
Vuông góc với
Chiều cưa véctơ mômen ngẫu lực là chiều sao cho đứng trên ngọn của véctơ mômen ngẫu lực nhìn thấy ngẫu lực có chiều?
Cùng kim đồng hồ
Sang trái
Sang phải
Ngược kim đồng hồ
Hai ngẫu lực tương đương nhau nếu chúng có?
Cùng véctơ mômen
Cùng độ lớn của ngẫu lực
Cùng vuông góc với một mặt phẳng
Cùng song song với một mặt phẳng
Có thể biến đổi một ngẫu lực đã cho thành một ngẫu lực mới có lực và cánh tay đòn khác nhau miễn là?
Cùng vuông góc với một mặt phẳng
Cùng song song với một mặt phẳng
Véctơ mômen ngẫu lực không đổi
Véctơ mômen ngẫu lực song song nhau
Kết quả tác dụng của ngẫu lực không đồi khi ta thay đổi vị trí của ngẫu lực?
Trong không gian
Trong mặt phẳng
Trong mặt phẳng vuông góc với nó
Trong mặt phẳng tác dụng của nó
Hợp các ngẫu lực cùng nằm trong một mặt phẳng được một ngẫu lực nằm trong mặt phẳng đã cho có đại số mômen bằng...... các ngẫu lực đã cho.
Tồng đại số mômen
Tổng trị số mômen
Đại số mômen
Trị số mômen
Hai lực trực đối nhau là hai lực cùng đường tác dụng, cùng trị số (cùng độ lớn) nhưng?
Song song nhau
Vuông góc nhau
ngược chiều nhau
đối nhau
Ký hiệu hai hệ lực tương đương?
\({F_1},{F_2}, \ldots ,{F_n} \equiv {K_1},{K_2}, \ldots ,{K_n}\)
\(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} , \ldots \overrightarrow {{F_n}} \equiv \overrightarrow {{K_1}} ,\overrightarrow {{K_2}} , \ldots ,\overrightarrow {{K_n}} \)
\(\left( {\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} , \ldots ,\overrightarrow {{F_n}} } \right) \equiv \left( {\overrightarrow {{K_1}} ,\overrightarrow {{K_2}} , \ldots ,\overrightarrow {{K_n}} } \right)\)
\(\left( {\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} , \ldots ,\overrightarrow {{F_n}} } \right) = \left( {\overrightarrow {{K_1}} ,\overrightarrow {{K_2}} , \ldots ,\overrightarrow {{K_n}} } \right)\)
Ký hiệu hệ lực?
\(\left( {\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} , \ldots ,\overrightarrow {{F_n}} } \right)\)
\({\vec F_1},\overrightarrow {{F_2}} , \ldots ,\overrightarrow {{F_n}} \)
\({F_1},{F_2}, \ldots ,{F_n}\)
\(\left( {{F_1},{F_2}, \ldots ,{F_n}} \right)\)
Điểm đặt của lực là điểm?
Trên vật có đường tác dưng lực đi qua
Giao nhau giữa các lực
Trên vật mà tại đó lực tác dụng vào vật
Trên vật
Phương chiều của lực là phương chiều chuyển động của...? ... từ trạng thái yên nghỉ dưới tác động của lực
Các chất điểm
Vật
Các vật
Chất điểm
Ký hiệu hệ lực cân bằng?
\(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \ldots + \overrightarrow {{F_n}} \equiv 0\)
\(\left( {{{\vec F}_1},\overrightarrow {{F_2}} , \ldots ,\overrightarrow {{F_n}} } \right) \equiv 0\)
\({\vec F_1},\overrightarrow {{F_2}} , \ldots ,\overrightarrow {{F_n}} \equiv 0\)
\(\left( {{{\vec F}_1},\overrightarrow {{F_2}} , \ldots ,\overrightarrow {{F_n}} } \right) = 0\)
Công thức xác định độ lớn của hợp lực \(\vec R = {\vec F_1} + \vec F\), ( \(\alpha \) là góc tạo bởi \({\vec F_1}\) và \({\vec F_2}\)?
\(R = {F_1}{\;^2} + {F_2}{\;^2} + 2{F_1}{F_2}{\rm{cos}}\alpha \)
\(R = \sqrt {F_1^2 + F_2^2} \)
\(R = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}{\rm{cos}}\alpha } \)
\(R = \sqrt {F_1^2 + F_2^2 - 2{F_1}{F_2}{\rm{cos}}\alpha } \)
Công thức xác định độ lớn của hợp lực \(\vec R = {\vec F_1} + \vec F\). Khi \({\vec F_1}\) và \({\vec F_2}\) vuông góc nhau \(\left( {\alpha = {{90}^ \circ }} \right)\) ?
\(R = {F_1}{\;^2} + {F_2}{\;^2}\)
\(R = {F_1} + {F_2}\)
\(R = \left| {F1 - F2} \right|\)
\(R = \sqrt {F_1^2 + F_2^2} \)
Công thức xác định độ lớn của hợp lực \(\vec R = {\vec F_1} + \vec F\). Khi \({\vec F_1}\) và \({\vec F_2}\) có cùng đường tác dưng lực \(\left( {\alpha = {0^0}} \right)\) ?
\(R = {F_1}{\;^2} + {F_2}{\;^2}\)
\({\rm{R}} = {{\rm{F}}_1} + {{\rm{F}}_2}\)
\(R = \left| {F1 - F2} \right|\)
\(R = \sqrt {F_1^2 + F_2^2} \)
Công thức xác định độ lớn của hợp lực \(\vec R = \overrightarrow {{F_1}} + \vec F\). Khi \({\vec F_1}\) và \({\vec F_2}\) ngược chiều nhau \(\left( {\alpha = {{180}^ \circ }} \right)\) ?
\({\rm{R}} = {{\rm{F}}_1}{\;^2} + {{\rm{F}}_2}{\;^2}\)
\({\rm{R}} = {{\rm{F}}_1} + {{\rm{F}}_2}\)
\(R = \left| {F1 - F2} \right|\)
\(R = \sqrt {F_1^2 + F_2^2} \)
Phản lực liên kết thanh có phương?
Vuông góc với thanh
Tạo với thanh một góc \(\alpha \)
Qua 2 điểm chịu lực (dọc theo thanh)
Vuông góc với nhau
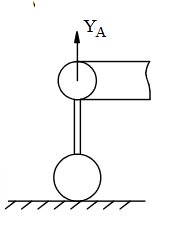
Chon hình có phản lực đúng
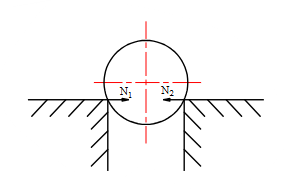
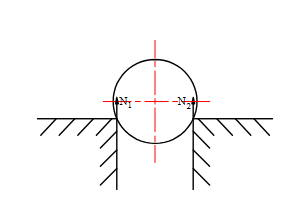
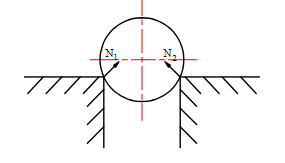
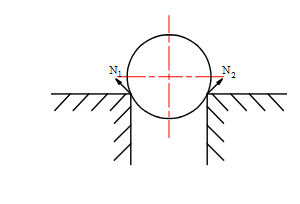
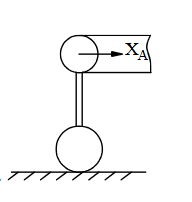
Chon hình có phản lực đúng
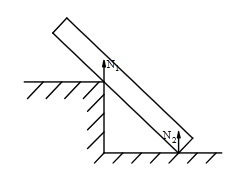
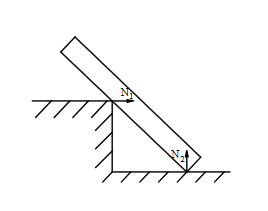
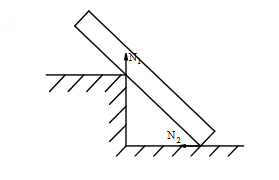
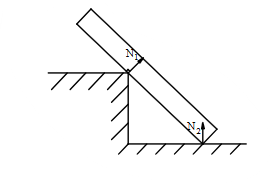
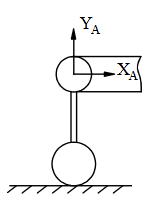
Chon hình có phản lực đúng
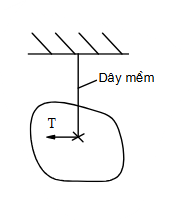
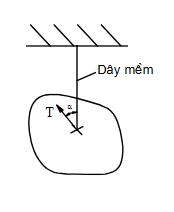
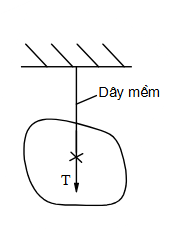
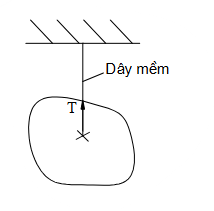
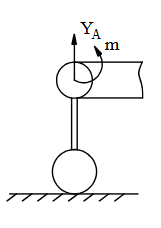
Chon hình có phản lực đúng trong liên kết cối sau?
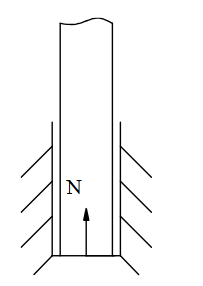
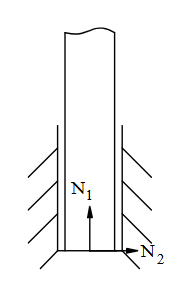
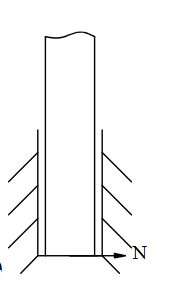
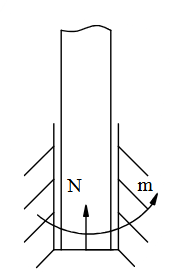
Chon hình có phản lực đúng trong liên kết ổ trụ dài?
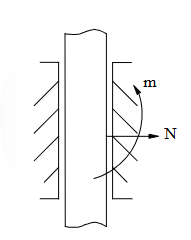
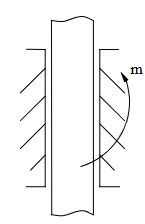
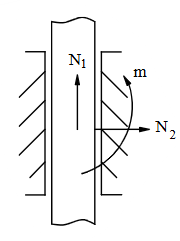
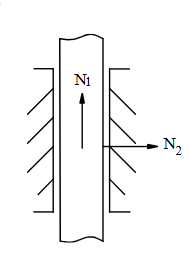
Chon hình có phản lực đúng cho liên kết sau?
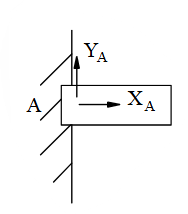
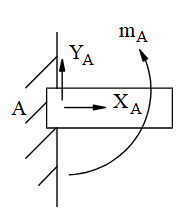
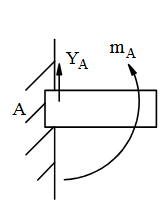
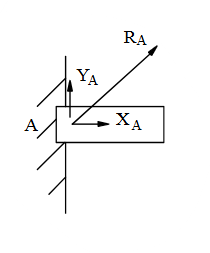
Chon hình có phản lực đúng cho liên kết sau?
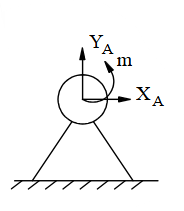
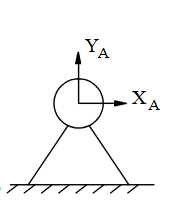
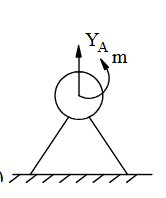
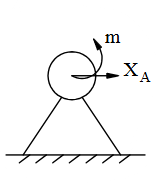
Chon hình có phản lực đúng cho liên kết sau?