30 Bài tập Câu hỏi lí thuyết Tốc độ phản ứng hóa học (có lời giải)
30 câu hỏi
Hoàn toàn có thể dựa vào sự thay đổi của đại lượng nào trong một đơn vị thời gian để đánh giá mức độ nhanh, chậm của phản ứng?
Nồng độ.
Chất xúc tác.
Nhiệt độ.
Áp suất.
Tốc độ phản ứng là
đại lượng đặc trưng cho sự tăng nồng độ của chất phản ứng.
đại lượng đặc trưng cho sự thay đổi nồng độ của chất phản ứng hoặc sản phẩm phản ứng trong một đơn vị thời gian.
đại lượng đặc trưng cho sự thay đổi áp suất của chất phản ứng hoặc sản phẩm phản ứng trong một đơn vị thời gian.
đại lượng đặc trưng cho sự thay đổi nhiệt độ của chất phản ứng hoặc sản phẩm phản ứng trong một đơn vị thời gian.
Yếu tố nào sau đây không làm ảnh hưởng đến tốc độ phản ứng?
Nồng độ.
Nhiệt độ.
Áp suất.
Khối lượng chất rắn.
Chất xúc tác là
chất làm giảm tốc độ phản ứng, nhưng không bị tiêu hao trong phản ứng.
chất làm tăng tốc độ phản ứng, nhưng bị tiêu hao trong phản ứng.
chất làm tăng tốc độ phản ứng nhưng không bị thay đổi cả lượng và chất sau khi phản ứng kết thúc.
chất làm thay đổi tốc độ phản ứng, nhưng bị tiêu hao không nhiều trong phản ứng.
Yếu tố nào sau đây luôn làm tăng tốc độ phản ứng?
Giảm nhiệt độ hệ phản ứng.
Tăng diện tích tiếp xúc giữa các chất phản ứng
Tăng lượng chất xúc tác.
Giảm áp suất hệ phản ứng.
Thông thường đối với các phản ứng có chất khí tham gia, khi tăng áp suất, tốc độ phản ứng
giảm.
không đổi.
tăng.
không xác định được.
Để xác định được mức độ phản ứng nhanh hay chậm người ta sử dụng khái niệm nào sau đây?
Tốc độ phản ứng.
Cân bằng hóa học.
Phản ứng một chiều.
Phản ứng thuận nghịch.
Thực hiện 2 thí nghiệm theo hình vẽ sau.
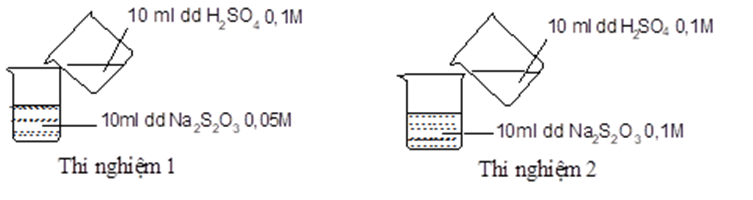
Ở thí nghiệm nào xuất hiện kết tủa trước?
Thí nghiệm 1 có kết tủa xuất hiện trước.
Thí nghiệm 2 có kết tủa xuất hiện trước.
Không xác định được.
Không có kết tủa xuất hiện.
Cho cùng một lượng kẽm (zinc) vào các cốc khác nhau chứa cùng một lượng dung dịch hydrochloric acid, trường hợp nào sẽ có tốc độ phản ứng nhanh nhất?
Kẽm ở dạng viên tròn nhỏ.
Kẽm ở dạng lá mỏng.
Kẽm ở dạng bột mịn, khuấy đều.
Kẽm ở dạng sợi, mảnh.
Cho các phản ứng sau:
(1) Phản ứng than cháy trong không khí.
(2) Phản ứng tạo gỉ sắt.
(3) Phản ứng nổ của khí bình gas.
(4) Phản ứng lên men rượu.
Phản ứng xảy ra với tốc độ nhanh nhất là
(1).
(2).
(3).
(4).
Chọn đáp án đúng nhất. Tốc độ tức thời của phản ứng là
sự thay đổi nồng độ của chất phản ứng hoặc sản phẩm trong một đơn vị thời gian.
tốc độ tính trung bình trong một khoảng thời gian phản ứng.
tốc độ phản ứng tại một thời điểm nào đó.
tốc độ phản ứng trong một khoảng thời gian nào đó.
Khi nồng độ chất tham gia phản ứng càng lớn thì
tốc độ phản ứng càng lớn.
tốc độ phản ứng càng giảm.
tốc độ phản ứng không thay đổi.
tốc độ phản ứng biến thiên liên tục.
Để hạn chế sự ôi thiu thực phẩm do các phản ứng của oxygen cũng như sự hoạt động của vi khuẩn, người ta thường bơm khí nào sau đây vào các túi đựng thực phẩm trước khi đóng gói?
O2.
N2.
CO2.
N2 hoặc CO2.
Tốc độ phản ứng tính theo định luật tác dụng khối lượng là
tốc độ phản ứng trung bình.
tốc độ tức thời của phản ứng tại một thời điểm.
tốc độ phản ứng trung bình tại một thời điểm.
tốc độ phản ứng tức thời trong một khoảng thời gian.
Nhận xét nào sau đây là không đúng về hằng số tốc độ phản ứng?
Giá trị của hằng số tốc độ phản ứng chỉ phụ thuộc vào nhiệt độ và bản chất các chất tham gia phản ứng.
Hằng số tốc độ của phản ứng càng lớn thì tốc độ của phản ứng đó càng lớn.
Hằng số tốc độ phản ứng có giá trị đúng bằng tốc độ phản ứng khi nồng độ các chất phản ứng bằng nhau và bằng 1M.
Hằng số tốc độ của phản ứng càng lớn thì tốc độ của phản ứng đó càng nhỏ.
Phản ứng của H2 và I2 là phản ứng đơn giản:
H2 (g) + I2 (g) → 2HI (g)
Theo định luật tác dụng khối lượng, tốc độ của phản ứng này được viết dưới dạng là
\[v = \frac{{\Delta {C_{{H_2}}}}}{{\Delta t}}\].
\[v = - \frac{{\Delta {C_{{I_2}}}}}{{\Delta t}}\].
\[v = k{C_{{H_2}}}{C_{{I_2}}}.\]
\[v = \frac{{\Delta {C_{HI}}}}{{\Delta t}}\] .
Nếu chia một vật thành nhiều phẩn nhỏ hơn thì tổng diện tích bề mặt sẽ
giảm đi.
tăng lên.
không thay đổi.
không xác định được.
Hệ số nhiệt độ Van’t Hoff được kí hiệu là
∝.
γ.
φ.
θ.
Chất làm giảm tốc độ phản ứng mà sau phản ứng nó không bị thay đổi về lượng và chất được gọi là
chất ức chế.
chất xúc tác.
chất hoạt hóa.
chất điện li.
Biện pháp nào sau đây không làm tăng diện tích bề mặt của khối chất?
Đập nhỏ khối chất.
Tạo lỗ xốp trong lòng khối chất.
Làm đầy các rãnh trên bề mặt khối chất.
Tạo nhiều đường rãnh trên bề mặt khối chất.
Năng lượng hoạt hóa là
năng lượng cần cung cấp cho phản ứng hóa học.
năng lượng tối thiểu cần cung cấp cho các hạt (nguyên tử, phân tử hoặc ion) để va chạm giữa chúng gây ra phản ứng hóa học.
năng lượng tối đa có thể cung cấp cho các hạt (nguyên tử, phân tử hoặc ion) để gây ra phản ứng hóa học.
lượng nhiệt tỏa ra hoặc thu vào khi hình thành phản ứng hóa học.
Nhận xét nào sau đây là sai?
Khi nồng độ chất tan trong dung dịch tăng, tốc độ phản ứng tăng.
Với mọi phản ứng, khi tăng áp suất, tốc độ phản ứng tăng.
Chất xúc tác làm tăng tốc độ phản ứng.
Đối với phản ứng có sự tham gia của chất khí, khi áp suất tăng, tốc độ phản ứng tăng.
Phát biểu nào sau đây không đúng?
Tốc độ trung bình của phản ứng là tốc độ tính trung bình trong một khoảng thời gian phản ứng.
Tốc độ phản ứng có thể nhận giá trị dương hoặc âm.
Tốc độ tức thời của phản ứng là tốc độ phản ứng tại một thời điểm nào đó.
Tốc độ phản ứng đốt cháy cồn (alcohol) lớn hơn tốc độ của phản ứng gỉ sắt.
Cho phản ứng đơn giản xảy ra trong bình kín:
3H2(g) + N2 (g) ⟶ 2NH3 (g).
Tốc độ phản ứng thay đổi như thế nào nếu nồng độ H2 không đổi và nồng độ N2 tăng 2 lần?
Tăng 2 lần.
Tăng 4 lần.
Tăng 8 lần.
Tăng 6 lần.
Khi nhiệt độ tăng thêm 10oC, tốc độ phản ứng hoá học tăng thêm 2 lần. Tốc độ phản ứng sẽ giảm đi bao nhiêu lần nhiệt khi nhiệt độ giảm từ 70oC xuống 40oC?
8.
16.
32.
64.
Tốc độ của một phản ứng hóa học lớn nhất khoảng thời điểm nào?
Bắt đầu phản ứng.
Khi phản ứng được một nửa lượng chất so với ban đầu.
Gần cuối phản ứng.
Không xác định được.
Biểu đồ nào sau đây không biểu diễn sự phụ thuộc nồng độ chất tham gia với thời gian?
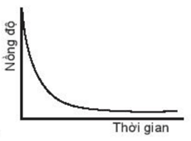
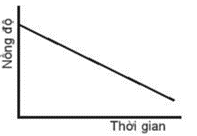
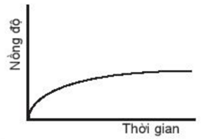
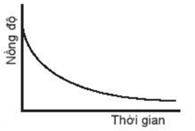
Cho phương trình phản ứng tổng quát sau:
2A + B → C
Tốc độ phản ứng tại một thời điểm được tính bằng biểu thức:
\[v = kC_A^2{C_B}\]
Hằng số tốc độ k phụ thuộc vào yếu tố nào sau đây?
Nồng độ của chất.
Nồng độ của chất B.
Nhiệt độ của phản ứng.
Thời gian xảy ra phản ứng.
Khí oxygen được điều chế trong phòng thí nghiệm bằng cách nhiệt phân potassium chlorate với xúc tác manganes dioxide. Để thí nghiệm thành công và rút ngắn thời gian tiến hành có thể dùng một số biện pháp sau:
(1) Trộn đều bột potassium chlorate và xúc tác.
(2) Nung ở nhiệt độ cao.
(3) Dùng phương pháp dời nước để thu khí oxygen.
(4) Nghiền nhỏ potassium chlorate.
Số biện pháp dùng để tăng tốc độ phản ứng là
2.
3.
4.
5.
Hình ảnh dưới đây minh họa ảnh hưởng của yếu tố nào tới tốc độ phản ứng:
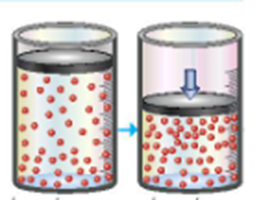
Diện tích bề mặt tiếp xúc.
Nhiệt độ.
Áp suất.
Chất xúc tác.








