31 câu hỏi
Các chuyên gia Y-tế ước tính số người nhiễm virus Zika kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ \(t\) là \(f\left( t \right) = 45{t^2} - {t^3},\left( {t = 0,1,2,...,25} \right)\). Nếu coi \(f\left( t \right)\)là một hàm xác định trên đoạn \(\left[ {0;25} \right]\) thì \(f'\left( t \right)\) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm \(t\). Tốc độ truyền bệnh sẽ lớn nhất vào ngày thứ mấy?
\(20\).
\(10\).
\(15\).
\(5\).
Một vật chuyển động theo quy luật \(s = - \frac{1}{2}{t^3} + 6{t^2}\) với \(t\) (giây)là khoảng thời gian từ khi vật bắt đầu chuyển động và \(s\) (mét) là quãng đường vật di chuyển trong thời gian đó. Hỏi trong khoảng thời gian \(6\) giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất vật đạt được bằng bao nhiêu?
\[24\,\left( {{\rm{m/s}}} \right)\].
\[108\,\left( {{\rm{m/s}}} \right)\].
\[64\,\left( {{\rm{m/s}}} \right)\].
\[18\,\left( {{\rm{m/s}}} \right)\].
Một vật chuyển động theo quy luật \(s = - \frac{1}{3}{t^3} + 6{t^2}\)với \(t\)(giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và \(s\)(mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 7 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
\(180\left( {{\rm{m/s}}} \right)\).
\(36\left( {{\rm{m/s}}} \right)\).
\(144\left( {{\rm{m/s}}} \right)\).
\(24\left( {{\rm{m/s}}} \right)\).
Một vật chuyển động theo quy luật \(s = - \frac{1}{2}{t^3} + 9{t^2}\) với \(t\) (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và \(s\) (mét) là quãng đường vật di chuyển trong khoảng thời gian đó. Hỏi trong khoảng thời gian \(10s\), kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
\(30m/s\).
\(400m/s\).
\(216m/s\).
\(54m/s\).
Các chuyên gia y tế ước tính số người nhiễm virus corona kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ \(t\) là \(f\left( t \right) = 45{t^2} - {t^3}\) với \(\left( {0 \le t \le 25} \right)\). Nếu coi \(f\left( t \right)\) là một hàm xác định trên đoạn \(\left[ {0;25} \right]\) thì hàm \(f'\left( t \right)\) được xem là tốc độ truyền bệnh tại thời điểm \(t\). Xác định ngày mà tốc độ truyền bệnh là lớn nhất.
\(15\).
\(20\).
\(10\).
\(5\).
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức \(G\left( x \right) = 0,025{x^2}\left( {30 - x} \right)\). Trong đó \(x\) là liều lượng thuốc được tiêm cho bệnh nhân (đơn vị miligam). Tính liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất.
\(15\)mg.
\(30\)mg.
\(25\)mg.
\(20\)mg.
Diện tích lớn nhất của hình chữ nhật nội tiếp đường tròn bán kính \(10{\rm{cm}}\) là:
\(160{\rm{c}}{{\rm{m}}^2}\).
\(100{\rm{c}}{{\rm{m}}^2}\).
\(200{\rm{c}}{{\rm{m}}^2}\).
\(80{\rm{c}}{{\rm{m}}^2}\).
Một vật chuyển động theo quy luật \(s = - \frac{1}{3}{t^3} + 6{t^2}\) với \(t\) (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và \(s\) (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu ?
\(144\) (m/s)
\(36\) (m/s)
\(243\) (m/s)
\(27\) (m/s)
Một chất điểm chuyển động có phương trình chuyển động là \[s = - {t^3} + 6{t^2} + 17t\], với \[t\left( s \right)\] là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và \[s\left( m \right)\] là quãng đường vật đi được trong khoảng thời gian đó. Trong khoảng thời gian 8 giây đầu tiên, vận tốc \[v\left( {m/s} \right)\]của chất điểm đạt giá trị lớn nhất bằng
\[29m/s\].
\[26m/s\].
\[17m/s\].
\[36m/s\].
Một chất điểm chuyển động có vận tốc tức thời \(v\left( t \right)\) phụ thuộc vào thời gian \(t\) theo hàm số \(v\left( t \right) = - {t^4} + 8{t^2} + 500\left( {{\rm{m/s}}} \right)\). Trong khoảng thời gian \(t = 0\left( {\rm{s}} \right)\) đến \(t = 5\left( {\rm{s}} \right)\) chất điểm đạt vận tốc lớn nhất tại thời điểm nào?
\(t = 4\).
\(t = 2\).
\(t = 0\).
\(t = 1\).
Một chất điểm chuyển động theo quy luật \(s = - {t^3} + 6{t^2} + 17t\), với \(t\) (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và \(s\)(mét) là quãng đường vật đi được trong khoảng thời gian đó. Khi đó vận tốc \(v\,\left( {m/s} \right)\)của chuyển động đạt giá trị lớn nhất trong khoảng \(8\) giây đầu tiên bằng
\(26\,m/s\).
\(36\,m/s\).
\(29\,m/s\).
\(17\,m/s\).
Một vật chuyển động theo quy luật \(s = \frac{1}{3}{t^3} - {t^2} + 9t\) với \[t\] (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong thời gian đó. Hỏi trong khoảng thời gian 10 giây kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu ?
\[89\left( {m/s} \right)\].
\[109\left( {m/s} \right)\].
\[71\left( {m/s} \right)\].
\[\frac{{25}}{3}\left( {m/s} \right)\].
Một chất điểm chuyển động theo quy luật \(s = - {t^3} + 6{t^2} + 17t\), với \(t\)(giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và \(s\)(mét) là quãng đường vật đi được trong khoảng thời gian đó. Khi đó vận tốc \(v\,\left( {m/s} \right)\)của chuyển động đạt giá trị lớn nhất trong khoảng \(8\)giây đầu tiên bằng
\(26\,m/s\).
\(36\,m/s\).
\(29\,m/s\).
\(17\,m/s\).
Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu \(h\left( m \right)\)của mực nước trong kênh tính theo thời gian \(t\left( h \right)\)được cho bởi công thức \(h = 3\cos \left( {\frac{{\pi t}}{6} + \frac{\pi }{3}} \right) + 12\)Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất?
\(t = 22\left( h \right)\).
\(t = 15\left( h \right)\).
\(t = 14\left( h \right)\).
\(t = 10\left( h \right)\).
, Một trang trại rau sạch mỗi ngày thu hoạch được một tấn rau. Mỗi ngày, nếu bán rau với giá \[30000\] đồng/kg thì hết rau sạch, nếu giá bán rau tăng \[1000\] đồng/kg thì số rau thừa tăng thêm \[20\] kg. Số rau thừa này được thu mua làm thức ăn chăn nuôi với giá \[2000\] đồng/kg. Hỏi tiền bán rau nhiều nhất trang trại có thể thu được mỗi ngày là bao nhiêu?
\[32400000\] đồng.
\[34400000\] đồng.
\[32420000\] đồng.
\[34240000\] đồng.
Một người bán buôn Thanh Long Đỏ ở Lập Thạch – Vĩnh Phúc nhận thấy rằng: Nếu bán với giá \(20000\)nghìn\[{\rm{/kg}}\] thì mỗi tuần có \(90\) khách đến mua và mỗi khách mua trung bình \(60\)\[{\rm{kg}}\]. Cứ tăng giá \(2000\) nghìn\[{\rm{/kg}}\] thì khách mua hàng tuần giảm đi \(1\) và khi đó khách lại mua ít hơn mức trung bình \(5\)\[{\rm{kg}}\], và như vậy cứ giảm giá \(2000\) nghìn\[{\rm{/kg}}\] thì số khách mua hàng tuần tăng thêm \(1\) và khi đó khách lại mua nhiều hơnmức trung bình \(5\)\[{\rm{kg}}\]. Hỏi người đó phải bán với giá mỗi \[{\rm{kg}}\] là bao nhiêu để lợi nhuận thu được hàng tuần là lớn nhất, biết rằng người đó phải nộp tổng các loại thuế là \(2200\) nghìn \[{\rm{/kg}}\]. (Kết quả làm tròn đến hàng nghìn)
\(16000\) nghìn\[{\rm{/kg}}\].
\(24000\) nghìn\[{\rm{/kg}}\].
\(22000\) nghìn\[{\rm{/kg}}\].
\(12000\) nghìn\[{\rm{/kg}}\].
Một người đàn ông muốn chèo thuyền ở vị trí \(A\) tới điểm \(B\) về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng \(3\,\,{\rm{km}}\) (như hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua sông để đến \(C\) và sau đó chạy đến \(B\), hay có thể chèo trực tiếp đến \(B\), hoặc anh ta có thể chèo thuyền đến một điểm \(D\) giữa \(C\) và \(B\) và sau đó chạy đến \(B\). Biết anh ấy có thể chèo thuyền \(6\,\,{\rm{km/}}\,{\rm{h}}\), chạy \(8\,\,{\rm{km/}}\,{\rm{h}}\) và quãng đường \(BC = 8\,\,{\rm{km}}\). Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Tính khoảng thời gian ngắn nhất (đơn vị: giờ) để người đàn ông đến \(B\).
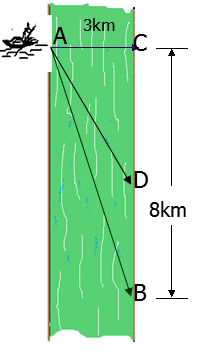
\(\frac{3}{2}\).
\(\frac{9}{{\sqrt 7 }}\).
\(\frac{{\sqrt {73} }}{6}\).
\(1 + \frac{{\sqrt 7 }}{8}\).
Ông An muốn xây một cái bể chứa nước lớn dạng khối hộp chữ nhật không nắp với thể tích \[288\]m3. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là 500000 đồng/m2. Nếu ông An biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất. Hỏi ông An trả chi phí thấp nhất để xây dựng bể đó là bao nhiêu?
108 triệu đồng.
90 triệu đồng.
168 triệu đồng.
54 triệu đồng.
Ông \(A\)dự định sử dụng hết \(5\,{{\rm{m}}^{\rm{2}}}\)kính để làm bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có thể tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hang phần trăm)?
\(1,01\,{{\rm{m}}^{\rm{3}}}\).
\(1,51\,{{\rm{m}}^{\rm{3}}}\).
\(1,33\,{{\rm{m}}^{\rm{3}}}\).
\(0,96\,{{\rm{m}}^{\rm{3}}}\).
Chi phí nhiên liệu của một chiếc tàu chạy trên sông được chia làm hai phần. Phần thứ nhất không phụ thuộc vào vận tốc và bằng \(480\) nghìn đồng trên \(1\) giờ. Phần thứ hai tỉ lệ thuận với lập phương của vận tốc, biết khi \(v = 10\) (km/giờ) thì phần thứ hai bằng \(30\) (nghìn đồng/ giờ). Hãy xác định vận tốc của tàu để tổng chi phí nhiên liệu trên \(1\,\,km\) đường sông là nhỏ nhất
\(10\) (km/giờ).
\(25\) (km/giờ).
\(15\) (km/giờ).
\(20\) (km/giờ).
Một bác nông dân cần xây dựng một hố ga không có nắp dạng hình hộp chữ nhật có dung tíchlà \(3200\,{\rm{c}}{{\rm{m}}^3}\), tỉ số giữa chiều cao của hố và chiều rộng của đáy bằng \(2\). Hãy xác định diện tích của đáy hố ga để khi xây tiết kiệm nguyên vật liệu nhất?
\(1200\,{\rm{c}}{{\rm{m}}^2}\).
\(120\,{\rm{c}}{{\rm{m}}^2}\).
\(160\,{\rm{c}}{{\rm{m}}^2}\).
\(1600\,{\rm{c}}{{\rm{m}}^2}\).
Một cửa hàng bán bưởi Đoan Hùng của Phú Thọ với giá bán mỗi quả là \[50.000\] đồng. Với giá bán này thì cửa hàng chỉ bán được khoảng \[40\] quả bưởi. Cửa hàng này dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi quả \[5000\] đồng thì số bưởi bán được tăng thêm là \[50\] quả. Xác định giá bán để cửa hàng đó thu được lợi nhuận lớn nhất, biết rằng giá nhập về ban đầu mỗi quả là \[30.000\] đồng.
.
.
.
.
Một hộp không nắp được làm từ một mảnh các tông theo mẫu. Hộp có đáy là một hình vuông cạnh \(x\,\left( {{\rm{cm}}} \right)\), chiều cao \(h\,\left( {{\rm{cm}}} \right)\) và có thể tích là \(500\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\).
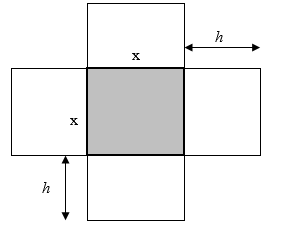
Tìm \(x\) sao cho diện tích mảnh các tông đó nhỏ nhất?
\(5\,{\rm{cm}}\).
\(100\,{\rm{cm}}\).
\(10\,{\rm{cm}}\).
\(20\,{\rm{cm}}\).
Một công ty bất động sản có \[50\] căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá \[2.000.000\]đồng một tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê, mỗi căn hộ thêm \[50.000\] đồng một tháng thì có thêm một căn hộ bị bỏ trống. Công ty đã tìm ra phương án cho thuê đạt lợi nhuận lớn nhất. Hỏi thu nhập cao nhất công ty có thể đạt được trong một tháng là bao nhiêu?
\[115.250.000\] .
\[101.250.000\] .
\[100.000.000\] .
\[100.250.000\].
Cho một tấm nhôm hình vuông cạnh \[12\left( {cm} \right)\]. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng \[x\left( {cm} \right)\], rồi gập tấm nhôm lại để được cái hộp không nắp (tham khảo hình vẽ bên). Tìm \[x\] để hộp nhận được có thể tích lớn nhất (giải thiết bề dày tấm tôn không đáng kể).

\[x = 2\].
\[x = 3\].
\[x = 4\].
\[x = 6\].
Từ một tấm tôn hình chữ nhật có kích thước \[40\]cm và \[60\]cm người ta cắt bỏ bốn hình vuông ở bốn góc để gập lại được một cái hộp không nắp.
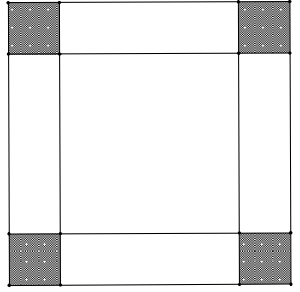
Để thể tích hộp đó lớn nhất thì cạnh của hình vuông cắt bỏ có giá trị gần với
\[7,85\]cm.
\[15\]cm.
\[3,92\]cm.
\[18\]cm.
Một người muốn xây một bể chứa có thể tích \(150{m^2}\) hình trụ. Vật liệu làm đáy, thành và nắp bể lần lượt có giá 100000 đồng/m2, 90000 đồng/m2 và 120000 đồng/m2. Tính chi phí thấp nhất để làm bể
\[15040000\]đồng.
\[15038000\]đồng.
\[15048000\]đồng.
\[15037000\]đồng.
Cho mạch điện xoay chiều \(RLC\) mắc nối tiếp có \(R\) thay đổi. Biết điện trở cuộn cảm \({Z_L} = 100\;\left( \Omega \right)\), điện trở của tụ điện là \({Z_C} = 40\left( \Omega \right)\) và hiệu điện thế hai đầu mạch là \[u = 120\sqrt 2 \cos 100\pi t{\rm{ }}\left( V \right)\]. Điện trở \(R\) phải có giá trị là bao nhiêu để công suất tiêu thụ của mạch đạt cực đại và giá tri cực đại của công suất là bao nhiêu?
\(R = 60\;\left( \Omega \right),\;{P_{\max }} = 120\;\left( {\rm{W}} \right)\).
\(R = 120\;\left( \Omega \right),\;{P_{\max }} = 60\;\left( {\rm{W}} \right)\).
\(R = 40\;\left( \Omega \right),\;{P_{\max }} = 180\;\left( {\rm{W}} \right)\).
\(R = 120\;\left( \Omega \right),\;{P_{\max }} = 180\;\left( {\rm{W}} \right)\).
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong \(t\)giờ được tính theo công thức \(c\left( t \right) = \frac{t}{{{t^2} + 1}}\)(mg/L). Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?
\(4\)giờ.
\(1\)giờ.
\(3\)giờ.
\(2\)giờ.
Thể tích \[V\] của \[1\,{\rm{kg}}\] nước ở nhiệt độ \(t\) (\(t\) nằm giữa \(0^\circ \,{\rm{C}}\) đến \(30^\circ \,{\rm{C}}\)) được cho bởi công thức \(V = 999,87 - 0,06426t + 0,0085043{t^2} - 0,0000679{t^3}\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\). Nhiệt độ \(t\) của nước gần nhất với giá trị nào dưới đây thì khối lượng riêng của nước là lớn nhất?
\(0^\circ \).
\( - 4^\circ \).
\(30^\circ \).
\(4^\circ \).
Để quảng bá cho sản phẩm A, một công ty dự định tổ chức quảng cáo theo hình thức quảng cáo trên truyền hình. Nghiên cứu của công ty cho thấy: nếu sau \(n\) lần quảng cáo được phát thì tỉ lệ người xem quảng cáo đó mua sản phẩm A tuân theo công thức \(P(n) = \frac{1}{{1 + 49{e^{ - 0,015n}}}}\). Hỏi cần phát ít nhất bao nhiêu lần quảng cáo để tỉ lệ người xem mua sản phẩm đạt trên \(30\% \) ?
\(202\).
\(203\).
\(206\).
\(207\).
