62 câu hỏi
Giá trị nhỏ nhất của hàm số \[y = 1 + x + \frac{4}{x}\] trên đoạn \[\left[ { - 3; - 1} \right]\] bằng
\[5\].
\[ - 4\].
\[ - 6\].
\[ - 5\].
Gọi \(M\), \(N\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {x^2}.{e^{ - x}}\) trên đoạn \(\left[ { - 1\,;1} \right]\). Tính tổng \(M + N\).
\(M + N = 3e\).
\(M + N = e\).
\(M + N = 2e - 1\).
\(M + N = 2e + 1\).
Tìm giá trị nhỏ nhất của hàm số \(y = \frac{{{x^2} + 3}}{{x - 1}}\) trên đoạn \(\left[ {2\,;4} \right]\).
\(\mathop {\min }\limits_{\left[ {2\,;4} \right]} y = - 3\).
\(\mathop {\min }\limits_{\left[ {2\,;4} \right]} y = \frac{{19}}{3}\).
\(\mathop {\min }\limits_{\left[ {2\,;4} \right]} y = 6\).
\(\mathop {\min }\limits_{\left[ {2\,;4} \right]} y = - 2\).
Giá trị nhỏ nhất của hàm số \(f\left( x \right) = x.{e^x}\)trên đoạn \(\left[ { - 2\,;\, - 1} \right]\) bằng
\(\frac{1}{e}.\)
\( - \frac{1}{e}.\)
\(\frac{2}{{{e^2}}}.\)
\( - \frac{2}{{{e^2}}}.\)
Cho \(a,b \in \mathbb{R}\), \(0 < a < b\), hàm số \(y = f(x)\) có đạo hàm trên \(\mathbb{R}\) thỏa mãn \(f'\left( x \right) < 0\), \(\forall x \in \left( {a;b} \right)\). Giá trị nhỏ nhất của hàm số đã cho trên đoạn \(\left[ {a\,;\,b} \right]\) bằng
>
\(f\left( b \right)\).
\(f\left( {\frac{{a + b}}{2}} \right)\).
\(f\left( a \right)\).
\(f\left( {\sqrt {ab} } \right)\).
Tìm giá trị lớn nhất của hàm số \(f(x) = {e^{x + 1}} - 2\) trên [0;3].
\({e^4} - 2\).
\({e^2} - 2\).
\(e - 2\).
\({e^3} - 2\).
Giá trị lớn nhất của hàm số \(f\left( x \right) = \frac{{ - {x^2} - 4}}{x}\)trên đoạn \(\left[ {\frac{3}{2};\,4} \right]\)là
\( - 2\).
\( - 4\).
\( - \frac{{25}}{6}\).
\( - 5\).
Giá trị lớn nhất của hàm số \[f\left( x \right) = \left( {2x - 3} \right){{\rm{e}}^x}\] trên \[\left[ {0;3} \right]\] là
\[\mathop {\max }\limits_{\left[ {0;3} \right]} f\left( x \right) = {{\rm{e}}^3}\].
\[\mathop {\max }\limits_{\left[ {0;3} \right]} f\left( x \right) = 5{{\rm{e}}^3}\].
\[\mathop {\max }\limits_{\left[ {0;3} \right]} f\left( x \right) = 4{{\rm{e}}^3}\].
\[\mathop {\max }\limits_{\left[ {0;3} \right]} f\left( x \right) = 3{{\rm{e}}^3}\].
Tìm giá trị lớn nhất (max) và giá trị nhỏ nhất (min) của hàm số \(y = x + \frac{1}{x}\)trên đoạn \(\left[ {\frac{3}{2};\,3} \right]\).
\(\mathop {\max }\limits_{\left[ {\frac{3}{2};\,3} \right]} y = \frac{{10}}{3}\), \(\mathop {\min }\limits_{\left[ {\frac{3}{2};\,3} \right]} y = \frac{{13}}{6}\).
\(\mathop {\max }\limits_{\left[ {\frac{3}{2};\,3} \right]} y = \frac{{10}}{3}\), \(\mathop {\min }\limits_{\left[ {\frac{3}{2};\,3} \right]} y = 2\).
\(\mathop {\max }\limits_{\left[ {\frac{3}{2};\,3} \right]} y = \frac{{16}}{3}\), \(\mathop {\min }\limits_{\left[ {\frac{3}{2};\,3} \right]} y = 2\).
\(\mathop {\max }\limits_{\left[ {\frac{3}{2};\,3} \right]} y = \frac{{10}}{3}\), \(\mathop {\min }\limits_{\left[ {\frac{3}{2};\,3} \right]} y = \frac{5}{2}\).
Giá trị lớn nhất của hàm số \(y = \left( {2x - 1} \right) + \ln \left( {2x + 1} \right)\) trên đoạn \(\left[ { - \frac{1}{4};0} \right]\) bằng
\( - \frac{3}{2} - \ln 2\).
\( - 1\).
\(\ln 2\).
\(1 + \ln 3\).
Giá trị nhỏ nhất của hàm số \[f\left( x \right) = \frac{{{x^2} + 4}}{x}\]trên đoạn \(\left[ {1\,;\,4} \right]\)bằng
\[2\sqrt 2 .\]
\[5.\]
\[\frac{{13}}{3}.\]
\[4.\]
Giá trị lớn nhất của hàm số \(y = x\left( {2 - \ln x} \right)\) trên đoạn \(\left[ {2;3} \right]\) là
\(\mathop {\max }\limits_{x \in \left[ {2;3} \right]} y = {\rm{e}}\).
\(\mathop {\max }\limits_{x \in \left[ {2;3} \right]} y = 6 - 3\ln 3\).
\(\mathop {\max }\limits_{x \in \left[ {2;3} \right]} y = 4 - 2\ln 2\).
\(\mathop {\max }\limits_{x \in \left[ {2;3} \right]} y = 1\).
Tìm giá trị nhỏ nhất \(m\)của hàm số \(y = {x^2} + \frac{2}{x}\) trên đoạn \(\left[ {\frac{1}{2};2} \right]\).
\(m = \frac{{17}}{4}\)
\(m = 10\)
\(m = 5\)
\(m = 3\)
Giá trị nhỏ nhất của hàm số \(y = x\ln x\) trên khoảng \(\left( {0; + \infty } \right)\) bằng
\({e^{ - 1}}\).
\(e\).
\( - 1\).
\( - {e^{ - 1}}\).
Cho hàm số \(y = \frac{{{x^2} - 3{\rm{x}} + 3}}{{x - 1}}\). Gọi \[M\] và \[m\] lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ { - 1;\frac{1}{2}} \right]\). Tính tích \[M \cdot m.\]
\( - 3\).
\(\frac{{21}}{2}\).
\( - \frac{1}{2}\).
\(0\).
Cho hàm số \(f\left( x \right) = \frac{{2{x^3}}}{3} + \ln x\). Giá trị nhỏ nhất của hàm số \(g\left( x \right) = \frac{1}{x}f'\left( x \right)\) là
\(3\).
\(2\).
\(1\).
Giá trị khác.
Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[f\left( x \right) = 2x - 4\sqrt {6 - x} \] trên đoạn \(\left[ { - 3;6} \right]\). Tổng \(M + m\) có giá trị là
\( - 6\).
\( - 12\).
\( - 4\).
\(18\).
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số  trên đoạn
trên đoạn  là
là
A. 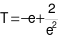 .
.
B. 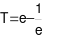 .
.
C.  .
.
D.  .
.
Gọi \(M\), \(m\)lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y = \frac{{{x^2} + 5}}{{x - 2}}\]trên \(\left[ { - 2;1} \right]\). Tính \(T = M + 2m\).
\[T = - \frac{{13}}{2}\].
\[T = - 10\].
\[T = - \frac{{21}}{2}\].
\[T = - 14\].
Tìm giá trị lớn nhất của hàm số \(y = \left( {{x^2} + 1} \right)\ln x\) trên đoạn \(\left[ {1;{\rm{e}}} \right]\).
\[\mathop {{\rm{max}}}\limits_{\left[ {1;{\rm{e}}} \right]} y = {{\rm{e}}^2} + 1\].
\[\mathop {{\rm{max}}}\limits_{\left[ {1;{\rm{e}}} \right]} y = 0\].
Không tồn tại.
\[\mathop {{\rm{max}}}\limits_{\left[ {1;{\rm{e}}} \right]} y = 4{{\rm{e}}^2} - 1\].
Tìm tập giá trị của hàm số \(y = \sqrt {x - 1} + \sqrt {9 - x} \)
\(T = \left[ {1;{\rm{ 9}}} \right]\).
\(T = \left[ {2\sqrt 2 ;{\rm{ 4}}} \right]\).
\(T = \left( {1;{\rm{ 9}}} \right)\).
\(T = \left[ {0;{\rm{ }}2\sqrt 2 } \right]\).
Giá trị lớn nhất của hàm số \(y = {\left( {x - 2} \right)^2}{{\rm{e}}^x}\) trên \(\left[ {1;3} \right]\) là
\[{\rm{e}}\].
\[0\].
\[{{\rm{e}}^3}\].
\[{{\rm{e}}^4}\].
Giá trị nhỏ nhất của hàm số \(y = \frac{{{x^2} - 5x + 1}}{x}\) trên đoạn \(\left[ {\frac{1}{2};3} \right]\) là
\( - 3\).
\( - \frac{5}{3}\).
\( - \frac{5}{2}\).
\(1\).
Giá trị nhỏ nhất của hàm số \(y = \ln \left( {{x^2} - 2x + 1} \right) - x\) trên đoạn \[\left[ {2;4} \right]\] là
\( - 2\).
\(2\ln 3 - 4\).
\( - 3\).
\(2\ln 2 - 3\).
Giá trị lớn nhất của hàm sô y = \(\frac{{{x^2} - 3x + 3}}{{x - 1}}\)trên đoạn \(\left[ { - 2;\frac{1}{2}} \right]\)là
\( - \frac{7}{2}\).
\( - \frac{{13}}{3}\).
\(1\).
\( - 3\).
Giá trị lớn nhất \(M\) và giá trị nhỏ nhất \(m\) của hàm số \(y = {x^2} - 2\ln x\) trên \(\left[ {{{\rm{e}}^{ - 1}}\,;\,{\rm{e}}} \right]\) là
\(M = {{\rm{e}}^2} - 2\), \(m = {{\rm{e}}^{ - 2}} + 2\).
\(M = {{\rm{e}}^{ - 2}} + 2\), \(m = 1\).
\(M = {{\rm{e}}^{ - 2}} + 1\), \(m = 1\).
\(M = {{\rm{e}}^2} - 2\), \(m = 1\).
Giá trị nhỏ nhất của hàm số \(y = x + \frac{9}{x}\)trên đoạn \(\left[ {2;4} \right]\)là
\(\mathop {\min }\limits_{\left[ {2;4} \right]} y = 6\).
\(\mathop {\min }\limits_{\left[ {2;4} \right]} y = \frac{{25}}{4}\).
\(\mathop {\min }\limits_{\left[ {2;4} \right]} y = - 6\).
\(\mathop {\min }\limits_{\left[ {2;4} \right]} y = \frac{{13}}{2}\).
Cho hàm số \(f\left( x \right) = {x^2} - x - \ln x\). Biết trên đoạn \(\left[ {1;e} \right]\) hàm số có GTNN là \(m\), và có GTLN là \(M\). Hỏi \(M + m\) bằng
\({e^2} - e + 1\).
\({e^2} - e - 1\).
\({e^2} - e\).
\(2{e^2} - e + 1\).
Tích của giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(f(x)\, = \,x + \frac{4}{x}\) trên đoạn \(\left[ {1\,;\,3} \right]\) bằng:
\(\frac{{52}}{3}\).
\(20\).
\(6\).
\(\frac{{65}}{3}\).
Tìm giá trị nhỏ nhất của hàm số \(y = x.{e^x}\) trên đoạn \[{\rm{[}}1;2].\]
\[e\].
\(2{e^2}\).
\( - \frac{1}{e}\).
\(\frac{e}{2}\).
Giá trị nhỏ nhất của hàm số \[y = {x^3} - 3x + 5\] trên đoạn \(\left[ {2;4} \right]\) là
\(\mathop {\min }\limits_{\left[ {2;\;4} \right]} y = 3\).
\(\mathop {\min }\limits_{\left[ {2;\;4} \right]} y = 7\).
\[\mathop {\min }\limits_{\left[ {2;{\rm{ }}4} \right]} y = 5.\]
\[\mathop {\min }\limits_{\left[ {2;{\rm{ }}4} \right]} y = 0.\]
Giá trị lớn nhất của hàm số \(f\left( x \right) = x\ln x\)trên đoạn \(\left[ {2;3} \right]\)bằng
\(f\left( 2 \right)\).
\(f\left( 3 \right)\).
\(f\left( {\frac{1}{{{e^2}}}} \right)\).
\(f\left( e \right)\).
Tìm giá trị nhỏ nhất của hàm số \(y = \frac{{x + 1}}{{x - 3}}\)trên đoạn \(\left[ { - 1\,;\,2} \right]\).
\(\mathop {\min }\limits_{x \in \left[ { - 1\,;\,2} \right]} {\mkern 1mu} y = 3\).
\(\mathop {\min }\limits_{x \in \left[ { - 1\,;\,2} \right]} {\mkern 1mu} y = - 3\).
\(\mathop {\min }\limits_{x \in \left[ { - 1\,;\,2} \right]} {\mkern 1mu} y = 0\).
\(\mathop {\min }\limits_{x \in \left[ { - 1\,;\,2} \right]} {\mkern 1mu} y = - 4\).
Giá trị nhỏ nhất của hàm số \(y = \left( {2x - 1} \right){e^x}\) trên đoạn \(\left[ { - 1;0} \right]\) bằng
\( - \frac{3}{e}\).
\( - \frac{2}{{\sqrt e }}\).
\( - 1\).
\(e\).
Tìm giá trị nhỏ nhất \(m\) của hàm số \(y = {x^3} - 3{x^2}\) trên \(\left[ { - 1;1} \right]\).
\(m = - 4\).
\(m = 0\).
\(m = - 2\).
\(m = - 5\).
Gọi \(m\) và \(M\) lần lượt là các giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(f\left( x \right) = {{\rm{e}}^{2 - 3x}}\) trên đoạn \(\left[ {0;2} \right]\). Mối liên hệ giữa M và m là
\(M - m = {\rm{e}}\).
\(m + M = 1\).
\(m{\rm{ }}.{\rm{ }}M = \frac{1}{{{{\rm{e}}^2}}}\).
\(\frac{M}{m} = {{\rm{e}}^2}\).
Tính tổng giá trị lớn nhất và nhỏ nhất của hàm số \[f\left( x \right) = {x^2} + \frac{2}{x}\] trên đoạn \(\left[ {\frac{1}{2}\,;\,2} \right]\).
8.
5.
4.
6.
Giá trị lớn nhất của hàm số \(y = x\left( {2 - \ln x} \right)\) trên đoạn \(\left[ {2;3} \right]\) bằng
3.
\(6 - 3\ln 3\).
\(4 - 2\ln 2\).
\({\rm{e}}\).
Giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = x + \sqrt {1 - {x^2}} \) lần lượt là
\(\sqrt 2 ;1\).
\(\sqrt 2 ;1\).
\(\sqrt 2 ; - 1\).
\(\sqrt 2 ;1\).
Gọi \(a,b\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \[y = {x^2} + {\log _2}\left( {2 - x} \right)\] trên đoạn \(\left[ { - 2;0} \right]\). Tổng \(a + b\) bằng
\(5\).
\(0\).
\(6\).
\(7\).
Gọi \(m\)và \(M\)lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = x - \sqrt {4 - {x^2}} \). Khi đó \(M - m\)bằng
\(4\).
\(2 - \sqrt 2 \).
\(2\left( {\sqrt 2 - 1} \right)\).
\(2\left( {\sqrt 2 + 1} \right)\).
Tìm giá trị lớn nhất của hàm số \(y = x + {{\rm{e}}^{2x}}\) trên đoạn \(\left[ {0\,;\,1} \right]\).
\[\mathop {\max }\limits_{x \in \left[ {0\,;\,1} \right]} y = {{\rm{e}}^2}\].
\[\mathop {\max }\limits_{x \in \left[ {0\,;\,1} \right]} y = 2{\rm{e}}\].
\[\mathop {\max }\limits_{x \in \left[ {0\,;\,1} \right]} y = 1\].
\(1\).
Tìm giá trị lớn nhất của hàm số \(y = {2^x}\) trên đoạn \(\left[ { - 1;2} \right]\) là
\(\frac{1}{2}\).
\(4\).
\(2\).
\( - 1\).
Giá trị nhỏ nhất của hàm số \(y = x{{\rm{e}}^x}\) trên \(\left[ { - 2;0} \right]\) bằng
\(0\).
\( - \frac{2}{{{{\rm{e}}^2}}}\).
\(f\left( 1 \right) = 4\).
Giá trị nhỏ nhất của hàm số \(f\left( x \right) = x.{e^x}\) trên đoạn \(\left[ { - 2\,;\, - 1} \right]\) bằng
\(\frac{1}{e}.\)
\( - \frac{1}{e}.\)
\(\frac{2}{{{e^2}}}.\)
\( - \frac{2}{{{e^2}}}.\)
Tìm giá trị nhỏ nhất của hàm số \(y = {e^{2x}} + 2{e^x}\) trên đoạn \(\left[ {0;\,2} \right]\).
\(\mathop {\min }\limits_{\left[ {0;\,2} \right]} y = 2{e^4} + 2{e^2}\).
\(\mathop {\min }\limits_{\left[ {0;\,2} \right]} y = {{\rm{e}}^4} + 2{{\rm{e}}^2}\).
\(\mathop {\min }\limits_{\left[ {0;\,2} \right]} y = 3\).
\(\mathop {\min }\limits_{\left[ {0;\,2} \right]} y = \frac{1}{{{{\rm{e}}^2}}} + \frac{2}{{\rm{e}}}\).
Tìm giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\)của hàm số \(y = {\log _2}\left( {x + 1} \right)\) trên đoạn \(\left[ {1;7} \right]\).
\(m = 1;M = 7\).
\(m = 1;M = 8\).
\(m = 1;M = 3\).
\(m = 3;M = 8\).
Cho hàm số \(y = {x^3} - \frac{3}{2}{x^2} + 1\). Gọi \(M\) là giá trị lớn nhất của hàm số trên khoảng \(\left( { - 25;\frac{{11}}{{10}}} \right)\). Tìm \(M\).
\(M = 1\).
\(M = \frac{1}{2}\).
\(M = 0\).
\(M = \frac{{129}}{{250}}\).
Giá trị lớn nhất của hàm số \(y = {\left( {x - 2} \right)^2}.{{\rm{e}}^x}\) trên đoạn \(\left[ {1;3} \right]\) là
\({{\rm{e}}^3}\).
\({\rm{e}}\).
\(0\).
\({{\rm{e}}^4}\).
Tìm giá trị nhỏ nhất của hàm số \[y = f\left( x \right) = 4{x^2} + \frac{1}{x} - 4\] trên khoảng \[\left( {0; + \infty } \right)\].
\[\mathop {{\rm{min}}}\limits_{\left( {{\rm{0; + }}\infty } \right)} f\left( x \right) = - 1\].
\[\mathop {{\rm{min}}}\limits_{\left( {{\rm{0; + }}\infty } \right)} f\left( x \right) = - 4\].
\[\mathop {{\rm{min}}}\limits_{\left( {{\rm{0; + }}\infty } \right)} f\left( x \right) = 7\].
\[\mathop {{\rm{min}}}\limits_{\left( {{\rm{0; + }}\infty } \right)} f\left( x \right) = - 3\].
Giá trị nhỏ nhất của hàm số \(y = {\log _2}^2x - 4{\log _2}x + 1\) trên \(\left[ {1;8} \right]\) là
\( - 2\).
\(1\).
\( - 3\).
\(2\).
Tìm giá trị nhỏ nhất của hàm số \(y = x - 5 + \frac{1}{x}\) trên khoảng \(\left( {0; + \infty } \right)\).
\[\mathop {\min }\limits_{\left( {0; + \infty } \right)} y = 2\].
\[\mathop {\min }\limits_{\left( {0; + \infty } \right)} y = - 4\].
\[\mathop {\min }\limits_{\left( {0; + \infty } \right)} y = - 3\].
\[\mathop {\min }\limits_{\left( {0; + \infty } \right)} y = - 5\].
Giá trị nhỏ nhất của hàm số \[y = x - 3\ln x\]trên đoạn \[\left[ {1;{\rm{e}}} \right]\]bằng
\[1\].
\[3 - 3\ln 3\].
\[{\rm{e}}\].
\[{\rm{e}} - 3\].
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = 2x - \frac{2}{{{x^2}}},\,\,\forall x \ne 0\). Giá trị nhỏ nhất của hàm số trên \(\left( {0; + \infty } \right)\) là
\(f\left( 1 \right)\).
\(f\left( 3 \right)\).
\(f\left( 0 \right)\).
\(f\left( { - 2} \right)\).
Giá trị nhỏ nhất, lớn nhất của hàm số \(y = x - \ln x\) trên đoạn \[\left[ {\frac{1}{2};\,{\rm{e}}} \right]\] theo thứ tự là
\[1\] và \({\rm{e}} - 1\).
\(\frac{1}{2} + \ln 2\) và \({\rm{e}} - 1\).
\[1\] và \({\rm{e}}\).
\[1\] và \(\frac{1}{2} + \ln 2\).
Giá trị nhỏ nhất của hàm số \(y = {x^2} + \frac{2}{x}\) với \(x > 0\) bằng
\(4\).
\(2\).
\(1\).
\(3\).
Giá trị lớn nhất của hàm số \(y = \ln x - \ln \left( {{x^2} + 1} \right)\) trên đoạn \(\left[ {\frac{1}{2};\,2} \right]\) khi:
\(x = 1\).
\(x = \frac{1}{2}\).
\(x = \frac{3}{2}\).
\(x = \frac{3}{4}\).
Giá trị lớn nhất của hàm số \(y = x\left( {1 - {x^2}} \right)\) trên khoảng \(\left( {0;\,1} \right)\) là
\(\frac{1}{9}\).
\(\frac{1}{{\sqrt 3 }}\).
\(0\).
\(\frac{{2\sqrt 3 }}{9}\).
Tìm giá trị lớn nhất của hàm số \[f(x) = {e^{x + 1}} - 2\] trên đoạn \[{\rm{[0;3]}}\].
\[{e^4} - 2\].
\[{e^2} - 2\].
\[e - 2\].
\[{e^3} - 2\].
Giá trị lớn nhất của hàm số \[y = \sqrt { - {x^2} + 4x} \] trên khoảng \[\left( {0;3} \right)\] là
4.
2.
0.
-2.
Tìm giá trị lớn nhất của hàm số \(y = \left( {{x^2} + 1} \right)\ln x\) trên đoạn \(\left[ {1;{\rm{e}}} \right]\).
\[\mathop {{\rm{max}}}\limits_{\left[ {1;{\rm{e}}} \right]} y = {{\rm{e}}^2} + 1\].
\[\mathop {{\rm{max}}}\limits_{\left[ {1;{\rm{e}}} \right]} y = 0\].
Không tồn tại.
\[\mathop {{\rm{max}}}\limits_{\left[ {1;{\rm{e}}} \right]} y = 4{{\rm{e}}^2} - 1\].
Giá trị lớn nhất của hàm số \(y = x + \frac{4}{{x - 1}}\) trên khoảng \(\left( { - \infty \,\,;\,\,1} \right)\) bằng
5.
\( - 1\).
3.
\( - 3\).
