31 câu hỏi
Gọi \(m\) là giá trị nhỏ nhất của hàm số \(y = x - 1 + \frac{4}{{x - 1}}\) trên khoảng \(\left( {1; + \infty } \right)\). Tìm \(m\).
\(m = 2\).
\(m = 5\).
\(m = 3\).
\(m = 4\).
Giá trị nhỏ nhất của biểu thức \(A = \frac{{3{x^2} - 8x + 6}}{{{x^2} - 2x + 1}}\)là
\(2\).
\(1\).
\( - 1\).
\( - 2\).
Tính giá trị nhỏ nhất của hàm số \(y = x + \frac{4}{{{x^2}}}\) trên khoảng \(\left( {0; + \infty } \right)\).
\(\mathop {\min }\limits_{\left( {0; + \infty } \right)} y = 5\).
\(\mathop {\min }\limits_{\left( {0; + \infty } \right)} y = 4\).
\(\mathop {\min }\limits_{\left( {0; + \infty } \right)} y = 3\).
\(\mathop {\min }\limits_{\left( {0; + \infty } \right)} y = 8\).
Tìm giá trị nhỏ nhất \(m\) của hàm số \(y = {x^3} + \frac{3}{x}\) trên \(\left( {0; + \infty } \right)\).
\(m = 4\sqrt[4]{3}\).
\(m = 2\sqrt 3 \).
\(m = 4\)
\(m = 2\)
Gọi \(m\) là giá trị nhỏ nhất của hàm số \(y = x - 1 + \frac{4}{{x - 1}}\) trên khoảng \(\left( {1; + \infty } \right)\). Tìm \(m\)?
\(m = 5\).
\(m = 4\).
\(m = 2\).
\(m = 3\).
Giá trị nhỏ nhất của hàm số \[y = \frac{{{x^2} - x + 1}}{{x - 1}}\] trên khoảng \[(1; + \infty )\] là
\[ - \frac{7}{3}\].
\[5\].
\[ - 1\].
\[3\].
Một chất điểm chuyển động theo phương trình \(S = - {t^3} + 3{t^2} - 2\), trong đó \(t\) tính bằng giây và \(S\) tính theo mét. Vận tốc lớn nhất của chuyển động chất điểm đó là
\(1\,\,m/s\).
\(3\,\,m/s\).
\(2\,\,m/s\).
\(4\,\,m/s\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;3} \right]\) và có đồ thị như hình bên. Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \(\left[ { - 1;3} \right]\). Giá trị của \(M - m\) bằng
![Cho hàm số y=f(x) liên tục trên đoạn [-1;3] và có đồ thị như hình bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho tr (ảnh 1)](https://video.vietjack.com/upload2/images/1754468606/1754468681-image1.png)
\(0\).
\(1\).
\(4\).
\(5\).
Cho hàm số \(y = f\left( x \right)\) liên tục và có bảng biến thiên trong đoạn \(\left[ { - 1;\,3} \right]\) như hình bên dưới. Gọi \(m\) là giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 1;\,3} \right]\). Tìm mệnh đề đúng?
![Cho hàm số y=f(x) liên tục và có bảng biến thiên trong đoạn [- 1;3]như hình bên dưới. Gọi m là giá trị nhỏ nhất của hàm số y=f(x) (ảnh 1)](https://video.vietjack.com/upload2/images/1754468606/1754468681-image2.png)
\(m = f\left( 0 \right)\).
\(m = f\left( 2 \right)\).
\(m = f\left( { - 1} \right)\).
\(m = f\left( 3 \right)\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 3\,;\,2} \right]\) và có bảng biến thiên như hình dưới. Gọi \(M\), \(m\) lần luợt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên \(\left[ { - 3\,;\,2} \right]\). Tính \(M - m\).
![Cho hàm số y=f(x) liên tục trên [- 3,2] và có bảng biến thiên như hình dưới. Gọi M, m lần luợt là giá trị lớn nhất và giá trị nhỏ nhất của h (ảnh 1)](https://video.vietjack.com/upload2/images/1754468606/1754468681-image3.png)
\(5\).
\(7\).
\(6\).
\(4\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên trên đoạn \(\left[ { - 4;1} \right]\) như sau
![Cho hàm số y=f(x) có bảng biến thiên trên đoạn [- 4;1] như sauKhi đó, mệnh đề nào sau đây đúng? (ảnh 1)](https://video.vietjack.com/upload2/images/1754468606/1754468681-image4.png)
Khi đó, mệnh đề nào sau đây đúng?
\(\mathop {\max }\limits_{\left[ { - 2;1} \right]} f\left( x \right) = 3\).
\(\mathop {\min }\limits_{\left[ { - 4;1} \right]} f\left( x \right) = - 2\).
\(\mathop {\max }\limits_{\left[ { - 4;1} \right]} f\left( x \right) = 1\).
\(\mathop {\min }\limits_{\left[ { - 2;1} \right]} f\left( x \right) = 0\).
Cho hàm số \(y = f\left( x \right)\) là hàm số liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ dưới đây
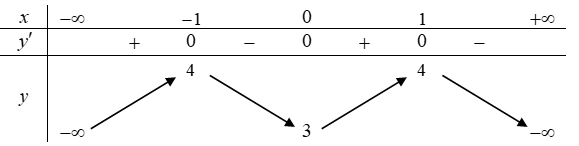
Khẳng định nào sau đây là khẳng định đúng?
\(\mathop {\min }\limits_\mathbb{R} y = 0\).
\(\mathop {\max }\limits_\mathbb{R} y = 1\).
\(\mathop {\min }\limits_\mathbb{R} y = 3\).
\(\mathop {\max }\limits_\mathbb{R} y = 4\).
Cho hàm số \(y = f(x)\)có đồ thị như hình vẽ bên. Gọi \(M,N\)lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn\(\left[ { - 2;2} \right]\). Tính giá trị biểu thức \(P = 3M - 2N\).
![Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Gọi M,N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [- 2;2]. Tính giá trị biểu thức P = 3M - 2N (ảnh 1)](https://video.vietjack.com/upload2/images/1754468606/1754468681-image6.png)
\(2\).
\(3\).
\(5\).
\(11\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau
![Cho hàm số y=f(x) có đồ thị như hình vẽ sauGiá trị lớn nhất của hàm số đã cho trên đoạn [-1;2] bằng (ảnh 1)](https://video.vietjack.com/upload2/images/1754468606/1754468681-image7.png)
Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ { - 1{\mkern 1mu} ;2} \right]\) bằng
\( - 1\).
\(2\).
\(0\).
\(4\).
Cho hàm số \(f\left( x \right)\) liên tục trên \(\left[ { - 1;5} \right]\) và có đồ thị trên đoạn \(\left[ { - 1;5} \right]\) như hình vẽ bên dưới. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ { - 1;5} \right]\)bằng
![Cho hàm số f(x) liên tục trên [-1;5] và có đồ thị trên đoạn [-1;5] như hình vẽ bên dưới. Tổng giá trị lớn nhất và giá trị nhỏ nhất c (ảnh 1)](https://video.vietjack.com/upload2/images/1754468606/1754468681-image8.png)
\( - 1\).
\(4\).
\(1\).
\(2\)
Cho hàm số \(f\left( x \right)\)liên tục trên đoạn \(\left[ { - 3;2} \right]\)và có đồ thị như hình vẽ bên. Gọi \(M,m\)lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \(\left[ { - 3;2} \right]\). Giá trị của \(M - m\)bằng:
![Cho hàm số f(x) liên tục trên đoạn [- 3;2] và có đồ thị như hình vẽ bên. Gọi M,m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn [-3;2] (ảnh 1)](https://video.vietjack.com/upload2/images/1754468606/1754468681-image9.png)
\(4\).
\(3\).
\(5\).
\(0\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
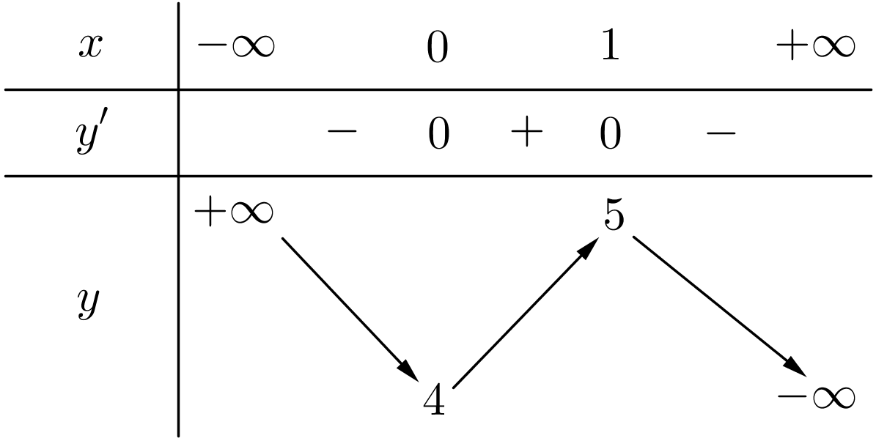
Giá trị nhỏ nhất của hàm số đã cho bằng
\(5\).
\(1.\)
\(4\).
Không tồn tại.
Cho hàm số \(y = f\left( x \right)\) có đồ thị trên đoạn \(\left[ { - 2\,;\,4} \right]\) như hình vẽ.
![Cho hàm số y=f(x) có đồ thị trên đoạn [-2;4] như hình vẽ.Tìm min f(x) trên [-2;4] (ảnh 1)](https://video.vietjack.com/upload2/images/1754468606/1754468681-image11.png)
Tìm \(\mathop {\min }\limits_{\left[ { - 2\,;\,4} \right]} f\left( x \right)\)
\( - 1\).
\( - 4\).
\(2\).
\( - 3\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị trên \(\left[ { - 2\,;\,4} \right]\) như hình vẽ, giá trị lớn nhất của \(f\left( x \right)\) trên \(\left[ { - 2;4} \right]\) là
![Cho hàm số y=f(x) có đồ thị trên [-2;4] như hình vẽ, giá trị lớn nhất của f(x) trên [-2;4] là (ảnh 1)](https://video.vietjack.com/upload2/images/1754468606/1754468681-image12.png)
4.
\( - 1\).
\(2\).
\(3\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 2\,;\,2} \right]\) và có đồ thị như hình vẽ bên dưới.
![Cho hàm số y=f(x) liên tục trên đoạn [-2;2] và có đồ thị như hình vẽ bên dưới.Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất c (ảnh 1)](https://video.vietjack.com/upload2/images/1754468606/1754468681-image13.png)
Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn \(\left[ { - 2\,;\,2} \right]\). Giá trị của \(M + m\) bằng
\[0\].
\[1\].
\(4\).
\[3\].
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ sau:
![Cho hàm số y=f(x) có bảng biến thiên như hình vẽ sau:Gọi M,m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số trên đoạn [- 2;6]. Tính P = 2M + m (ảnh 1)](https://video.vietjack.com/upload2/images/1754468606/1754468681-image14.png)
Gọi \(M,m\) lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số trên đoạn \(\left[ { - 2;6} \right]\) . Tính \(P = 2M + m\) .
\(P = 6\).
\(P = 7\).
\[P = 9\].
\(P = 8\).
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu đạo hàm như sau:
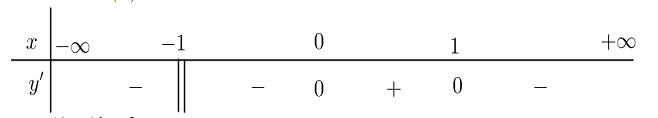
Mệnh đề nào sau đây đúng
\(\mathop {\min }\limits_{\left( { - 1;\, + \infty } \right)} f\left( x \right) = f\left( 0 \right)\).
\(\mathop {{\rm{max}}}\limits_{\left( {0;\, + \infty } \right)} f\left( x \right) = f\left( 1 \right)\).
\(\mathop {{\rm{max}}}\limits_{\left( { - 1;\,1} \right]} f\left( x \right) = f\left( 0 \right)\).
\(\mathop {\min }\limits_{\left( { - \infty ;\, - 1} \right)} f\left( x \right) = f\left( { - 1} \right)\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(y = f'\left( x \right)\) liên tục trên \(\mathbb{R}\) và đồ thị của hàm số \(f'\left( x \right)\) trên đoạn \[\left[ { - 2;6} \right]\] như hình vẽ bên.
![Cho hàm số y=f(x) có đạo hàm y=f'(x) liên tục trên R và đồ thị của hàm số f'(x) trên đoạn [-2;6] (ảnh 1)](https://video.vietjack.com/upload2/images/1754468606/1754468681-image16.png)
Tìm khẳng định đúng trong các khẳng định sau.
\(\mathop {\max }\limits_{[ - 2;6]} f\left( x \right) = f\left( { - 2} \right).\)
\(\mathop {\max }\limits_{[ - 2;6]} f\left( x \right) = f\left( 6 \right).\)
\(\mathop {\max }\limits_{[ - 2;6]} f\left( x \right) = \max \left\{ {f\left( { - 1} \right),f\left( 6 \right)} \right\}.\)
\(\mathop {\max }\limits_{[ - 2;6]} f\left( x \right) = f\left( { - 1} \right).\)
Một chất điểm chuyển động theo quy luật \[S\left( t \right) = 1 + 3{t^2} - {t^3}\]. Vận tốc của chuyển động đạt giá trị lớn nhất khi \[t\] bằng bao nhiêu
\[t = 2\].
\[t = 1\].
\[t = 3\].
\[t = 4\].
Một vật chuyển động theo quy luật \[s = - \frac{1}{3}{t^3} + 6{t^2}\] với \[t\] (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và \[s\] (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian \[9\] giây kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được là
\[243\left( {{\rm{m/s}}} \right)\].
\[27\left( {{\rm{m/s}}} \right)\].
\[36\left( {{\rm{m/s}}} \right)\].
\[144\left( {{\rm{m/s}}} \right)\].
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức \(f\left( x \right) = 0,025{x^2}\left( {30 - x} \right)\), trong đó \(x\) (miligam) là liều lượng thuốc được tiêm cho bệnh nhân. Khi đó, liều lượng thuốc được tiêm cho bệnh nhân để huyết áp giảm nhiều nhất là
\(20\)miligam.
\(10\)miligam.
\(15\)miligam.
\(30\)miligam.
Một cơ sở sản xuất khăn mặt đang bán mỗ chiếc khăn với giá \(30.000\) đồng một chiếc và mỗi tháng cơ sở bán được trung bình \(3000\) chiếc khăn. Cơ sở đang có kế hoạch tăng giá bán để có lợ nhuận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá \[30.000\]đồng mà cứ tăng giá thêm \(1.000\) đồng thì mỗi tháng sẽ bán ít hơn \(100\) chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là \(18.000\) đồng. Hỏi cơ sở sản xuất phải bán là mức giá bao nhiêu để đạt lợi nhuận lớn nhất.
\(43.000\) đồng.
\(36.000\) đồng.
\(39.000\) đồng.
\(42.000\) đồng.
Một vật chuyển động theo quy luật \(s = - \frac{1}{3}{t^3} + 6{t^2}\) với \(t\) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và \(s\) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
243.
144.
27.
36.
Một con cá hồi bơi ngược dòng nước để vượt một khoảng cách \(300\) km, vận tốc của dòng nước là \(6\) (km/h). Giả sử vận tốc bơi của cá khi nước yên lặng là \(v\) (km/h). Năng lượng tiêu hao của cá trong \(t\) giờ được tính theo công thức \(E = c\,{v^3}t\), \(c\) là hằng số cho trước, đơn vị của \(E\) là Jun. Vận tốc \(v\) của cá khi nước đứng yên để năng lượng của cá tiêu hao ít nhất là
\(8\) (km/h).
\(12\) (km/h).
\(10\) (km/h).
\(9\) (km/h).
Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng \[Q\left( n \right) = 480 - 20n\] (gam). Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?
\[12\].
\[14\].
\[10\].
\[18\].
Một vật chuyển động theo quy luật \(s = - \frac{1}{3}{t^3} + 6{t^2}\) với \(t\) (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và \(s\) (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu ?
\(144\) (m/s).
\(36\) (m/s).
\(243\) (m/s).
\(27\) (m/s).
