10 Bài tập Số đo của góc lượng giác và hệ thức Chasles (có lời giải)
10 câu hỏi
Công thức biểu thị số đo của các góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác có số đo bằng 120° là
–120° + k360° (k ∈ ℤ);
120° + k360° (k ∈ ℤ);
120° + k180° (k ∈ ℤ);
–120° + k180° (k ∈ ℤ).
Cho góc hình học uOv = 45°. Xác định số đo của góc lượng giác (Ou, Ov) trong hình vẽ sau:
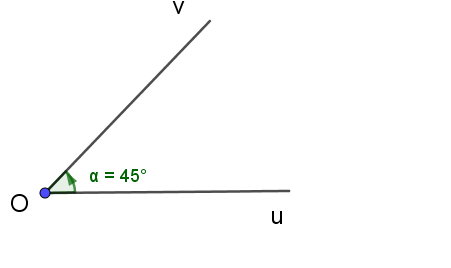
60°;
– 45°;
45°;
– 60°.
Cho góc hình học uOv = 75°. Xác định số đo của góc lượng giác (Ou, Ov) trong hình vẽ sau:
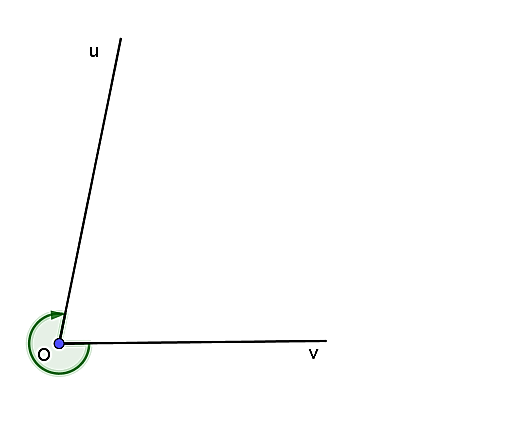
315°;
–315°;
285°;
–285°.
Xác định số đo của góc lượng giác (Ou, Ov) trong hình vẽ sau:
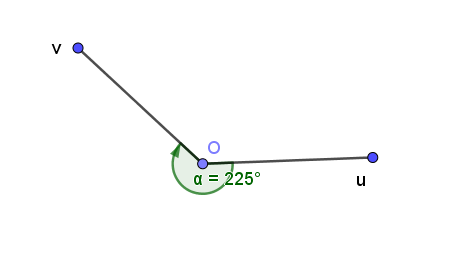
225°;
–225°;
135°;
–135°.
Cho góc lượng giác (OA, OB) có số đo bằng \(\frac{\pi }{5}\). Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác (OA, OB)?
A. \(\frac{{6\pi }}{5}\);
B. \(\frac{{ - 11\pi }}{5}\);
C. \(\frac{{9\pi }}{5}\);
\(\frac{{31\pi }}{5}.\)
Cho góc lượng giác (OA, OB) có số đo 395°. Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác (OA, OB)?
45°;
–35°;
35°;
–45°.
Trong khoảng thời gian từ 0 giờ đến 2 giờ 30 phút, kim phút quét một góc lượng giác bằng
A. – 900°;
B. – 1 000°;
C. 900°;
– 1 000°.
Các góc lượng giác (Ox, Ou) và (Ox, Ov) có số đo lần lượt là –270° và 135°. Số đo của góc lượng giác (Ou, Ov) là
50° + m360°, m ∈ ℤ;
45° + m360°, m ∈ ℤ;
–45° + m360°, m ∈ ℤ;
–50° + m360°, m ∈ ℤ.
Cho góc lượng giác (Ou, Ov) có số đo là \(\frac{{3\pi }}{4}\), góc lượng giác (Ou, Ow) có số đo là \(\frac{{5\pi }}{4}\). Số đo của góc lượng giác (Ov, Ow) là
\(\frac{{ - \pi }}{2}\) + k2π (k ∈ ℤ);
\(\frac{\pi }{2}\) + k2π (k ∈ ℤ);
\(\frac{{ - \pi }}{3}\) + k2π (k ∈ ℤ);
\(\frac{\pi }{3}\) + k2π (k ∈ ℤ).
Cho góc lượng giác (Ou, Ov) có số đo là \(\frac{{ - 5\pi }}{4}\), góc lượng giác (Ou, Ow) có số đo là \(\frac{{15\pi }}{4}\). Tìm số đo của góc lượng giác (Ov, Ow) biết rằng 4π < sđ (Ov, Ow) < 6π.
</>
4π;
7π;
5π;
6π.








