Quiz

Trắc nghiệm Toán 9 Bài Ôn tập chương (có đáp án): Hệ thức lượng trong tam giác vuông (phần 2)

Admin34 câu hỏiToánLớp 9

Bắt đầu ngay

34 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

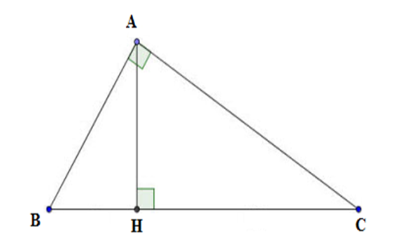
Cho tam giác ABC vuông tại A, chiều cao AH. Chọn câu sai.

A. $A H^{2} = B H . C H$

B. $A B^{2} = B H . B C$

C. $\frac{1}{A H^{2}} = \frac{1}{A B^{2}} + \frac{1}{A C^{2}}$

D. AH. AB = BC. AC

2. Nhiều lựa chọn

Cho hình vẽ sau:

Cho hình vẽ sau Chọn câu sai sin B=AH/AB B. cos C= AC/ BC C. tan B= AC/ AB (ảnh 1)

Chọn câu sai.

A. sin B = $\frac{A H}{A B}$

B. cos C = $\frac{A C}{B C}$

C. tan B = $\frac{A C}{A B}$

D. tan C = $\frac{A H}{A C}$

3. Nhiều lựa chọn

Chọn câu đúng nhất. Nếu $α$ là một góc nhọn bất kì, ta có:

A. $\sin^{2} α + c o s^{2} α = 1$

B. $\tan α . c o t α = 1$

C. $\tan α = \frac{\sin α}{\cos α}$

D. Cả A, B, C đều đúng.

4. Nhiều lựa chọn

Cho $α; β$ là hai góc nhọn bất kì $α < β$ . Chọn câu đúng.

A. sin $α$ > sin $β$ .

B. cos $α$ < cos $β$ .

C. tan $α$ < tan $β$ .

D. cot $α$ < cot $β$ .

5. Nhiều lựa chọn

Tính giá trị của x trên hình vẽ:

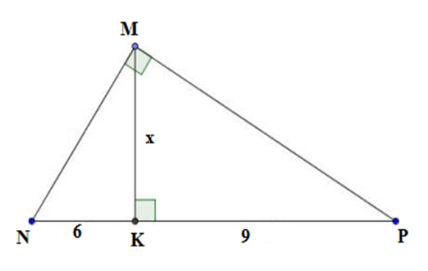
Tính giá trị của x trên hình vẽ 2 căn bậc hai của 6 B. căn bậc hai của 6 (ảnh 1)

A. $2 \sqrt{6}$

B. $\sqrt{6}$

C. $3 \sqrt{6}$

D. 27

6. Nhiều lựa chọn

Cho tan a = 3. Khi đó cot a bằng?

A. $\frac{1}{3}$

B. 3

C. $\sqrt{3}$

D. $\frac{1}{2}$

7. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có AB = 3cm, BC = 5cm. AH là đường cao. Tính BH, CH, AC và AH.

A. BH = 2cm, CH = 3,2cm, AC = 4cm, AH = 2,4cm

B. BH = 1,8cm; CH = 3,2cm; AC = 4cm; AH = 2,4cm

C. BH = 1,8cm; CH = 3,2cm; AC = 3cm; AH = 2,4cm

D. BH = 1,8cm; CH = 3,2cm; AC = 4cm; AH = 4,2cm

8. Nhiều lựa chọn

Giải tam giác vuông ABC, biết $\hat{A} = 90^{0}$ và BC = 50cm; $\hat{B} = 48^{0}$ (làm tròn đến chữ số thập phân thứ nhất).

A. AC = 37,2cm; AB = 33,4cm; $\hat{C} = 32^{0}$

B. AC = 37,2cm; AB = 33,5cm; $\hat{C} = 42^{0}$

C. AB = 37,2cm; AC = 33,5cm; $\hat{C} = 42^{0}$

D. AC = 37,2cm; AB = 33,5cm; $\hat{C} = 42^{0}$

9. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có AB = 21cm; $\hat{C} = 40^{0}$ , phân giác BD (D thuộc AC). Độ dài phân giác BD là? (kết quả làm tròn đến chữ số thập phân thứ nhất).

A. 21,3cm

B. 24cm

C. 22,3cm

D. 23,2cm

10. Nhiều lựa chọn

Cho tam giác ABC vuông tại A, có AC = 14, BC = 17. Khi đó tan B bằng:

A. $\frac{\sqrt{93}}{14}$

B. $14 \sqrt{93}$

C. $\frac{14 \sqrt{93}}{93}$

D. $\frac{14}{17}$

11. Nhiều lựa chọn

Giá trị biểu thức $\sin^{4} α + c o s^{4} α + 2 \sin^{2} α . c o s^{2} α$ là?

A. 1

B. 2

C. 4

D. −1

12. Nhiều lựa chọn

Cạnh bên của tam giác ABC cân tại A dài 20cm, góc ở đáy là $50^{0}$ . Độ dài cạnh đáy của tam giác cân là? (kết quả làm tròn đến chữ số thập phân thứ nhất).

A. 25cm

B. 25,7cm

C. 26cm

D. 12,9cm

13. Nhiều lựa chọn

Cho hình vẽ, tìm x.

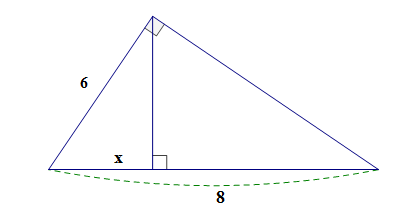
Cho hình vẽ, tìm x. x=0,75 x=4,5 x= 4 căn bậc hai của 3 D. x= 4 (ảnh 1)

A. x = 0,75

B. x = 4,5

C. x = $4 \sqrt{3}$

D. x = 4

14. Nhiều lựa chọn

Cho $\tan α = \frac{3}{4}$ . Giá trị biểu thức: $M = \frac{\sin α - 2 \cos α}{\sin α - \cos α}$

A. M = 5

B. M = $- \frac{5}{4}$

C. M = −5

D. M = $\frac{1}{5}$

15. Nhiều lựa chọn

Tìm x; y trong hình vẽ sau:

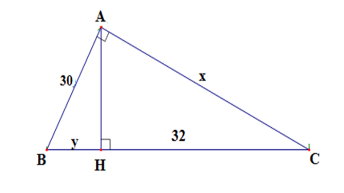
Tìm x; y trong hình vẽ sau: x=30; y=28 B. x= 2 căn bậc hai của 481 (ảnh 1)

A. x = 30; y = 28

B. x = $2 \sqrt{481}$ ; y = $\frac{225}{8}$

C. x = 18; y = 40

D. x = 40; y = 18

16. Nhiều lựa chọn

Tính số đo góc nhọn x, biết $\cos^{2} x - \sin^{2} x = \frac{1}{2}$

A. $45^{0}$

B. $30^{0}$

C. $60^{0}$

D. $90^{0}$

17. Nhiều lựa chọn

Cho $∆$ ABC vuông tại A. Biết $\frac{A B}{A C} = \frac{5}{7}$ . Đường cao AH = 15cm. Tính HC.

A. $\frac{15 \sqrt{74}}{7}$

B. $3 \sqrt{74}$ cm

C. 22cm

D. 21cm

18. Nhiều lựa chọn

Cho $∆$ ABC vuông tại A, AB = 12cm, AC = 16cm, tia phân giác AD, đường cao AH. Tính HD.

A. $\frac{48}{35}$ cm

B. 7,2cm

C. $\frac{60}{7}$ cm

D. $\frac{48}{25}$ cm

19. Nhiều lựa chọn

Tính giá trị $C = {(3 \sin α + 4 \cos α)}^{2} + {(4 \sin α - 3 \cos α)}^{2}$

A. 25

B. 16

C. 9

D. 25 + 48sin $α$ .cos $α$

20. Nhiều lựa chọn

Cho biết $\tan α = \frac{2}{3}$ . Tính giá trị biểu thức: $M = \frac{\sin^{3} α + 3 \cos^{3} α}{27 \sin^{3} α - 25 \cos^{3} α}$

A. $\frac{89}{891}$

B. $\frac{89}{159}$

C. $\frac{89}{459}$

D. $- \frac{89}{459}$

21. Nhiều lựa chọn

Sắp xếp theo thứ tự tăng dần: $c o t 70^{0}$ ; $\tan 33^{0}$ ; $c o t 55^{0}$ ; $\tan 28^{0}$ ; $c o t 40^{0}$

A. $\tan 28^{0}$ < $\tan 33^{0}$ < $c o t 40^{0}$ < $c o t 55^{0}$ < $c o t 70^{0}$

B. $\tan 28^{0}$ < $c o t 70^{0}$ < $\tan 33^{0}$ < $c o t 55^{0}$ < $c o t 40^{0}$

C. $c o t 70^{0}$ < $\tan 28^{0}$ < $\tan 33^{0}$ < $c o t 55^{0}$ < $c o t 40^{0}$

D. $c o t 70^{0}$ > $\tan 28^{0}$ > $\tan 33^{0}$ > $c o t 55^{0}$ > $c o t 40^{0}$

22. Nhiều lựa chọn

Cho tam giác ABC vuông tại A. Tính $A = \sin^{2} B + \sin^{2} C - \tan B . \tan C$

A. 0

B. 1

C. −1

D. 2

23. Nhiều lựa chọn

Cho đoạn thẳng AB = 2a và trung điểm O của nó. Trên nửa mặt phẳng bờ AB vẽ các tia Ax, By vuông góc với AB. Qua O vẽ một tia cắt Ax tại M sao cho $\hat{A O M} = α < 90^{0}$ . Qua O vẽ tia thứ hai cắt By tại N sao cho $\hat{M O N} = α < 90^{0}$ . Khi đó, diện tích tam giác MON là:

A. $\frac{a^{2}}{2 \sin α . \cos α}$

B. $\frac{a^{2}}{\sin α . \cos α}$

C. $\frac{a}{2 \sin α . \cos α}$

D. $\frac{2 a^{2}}{\sin α . \cos α}$

24. Nhiều lựa chọn

Cho hình thang cân ABCD (AB // CD); CD = 2AD = 2AB = 8. Tính diện tích của hình thang đó.

A. $12 \sqrt{2}$

B. $12 \sqrt{3}$

C. 12

D. $12 \sqrt{6}$

25. Nhiều lựa chọn

Cho hình thang vuông ABCD có hai đáy AB = 12cm, DC = 16cm, cạnh xiên AD = 8cm. Tính các góc và cạnh góc vuông của hình thang.

A. $B C = 3 \sqrt{3} c m$ , $\hat{A} = 120^{0}$ , $\hat{D} = 60^{0}$

B. $B C = 4 \sqrt{3} c m$ , $\hat{A} = 120^{0}$ , $\hat{D} = 60^{0}$

C. $B C = 3 \sqrt{3} c m$ , $\hat{A} = 135^{0}$ , $\hat{D} = 45^{0}$

D. $B C = 4 \sqrt{3} c m$ , $\hat{A} = 135^{0}$ , $\hat{D} = 45^{0}$

26. Nhiều lựa chọn

Cho tứ giác ABCD có AB = AC = AD = 20cm, $\hat{B} = 60^{0}$ và $\hat{A} = 90^{0}$ . Kẻ BE DC kéo dài.

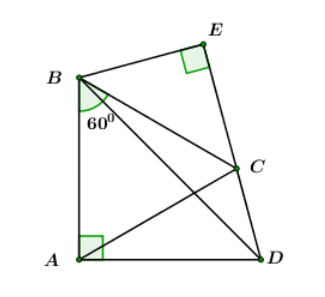
Cho tứ giác ABCD có AB = AC = AD = 20cm, góc B=60 độ , góc A= 90 độ Kẻ BE DC kéo dài. (ảnh 1)

Tính BE?

A. BE = $10 \sqrt{2}$ cm

B. BE = 10cm

C. BE = $10 \sqrt{3}$ cm

D. BE = 20cm

27. Nhiều lựa chọn

Bạn An đang học vẽ hình bằng phần mềm máy tính. An vẽ hình một ngôi nhà với phần mái có dạng hình tam giác cân (hình vẽ bên). Biết góc tạo bởi phần mái và mặt phẳng nằm ngang là $30^{0}$ , chiều dài mỗi bên dốc mái là 3,5m. Tính gần đúng bề rộng của mái nhà.

A. 6,52m

B. 6,06m

C. 5,86m

D. 5,38m

28. Nhiều lựa chọn

Cho tam giác ABC có diện tích là $900 c m^{2}$ . Điểm D ở giữa BC sao cho BC = 5DC, điểm E ở giữa AC sao cho AC = 4AE, hai điểm F, G ở giữa BE sao cho BE = 6GF = 6GE. Tính diện tích tam giác DGF.

A. 80 $c m^{2}$

B. 90 $c m^{2}$

C. 100 $c m^{2}$

D. 120 $c m^{2}$

29. Nhiều lựa chọn

Cho tam giác ABC vuông tại A, AB = 15cm; AC = 20cm. Phân giác của góc A cắt BC tại E.

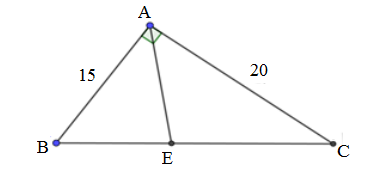
Cho tam giác ABC vuông tại A, AB = 15cm; AC = 20cm. Phân giác của góc A cắt BC tại E. (ảnh 1)

Giải tam giác ABC:

A. BC = 25; $\hat{B} = 36^{0} 52'$ ; $\hat{C} = 53^{0} 8'$

B. BC = 25; $\hat{B} = 53^{0} 8'$ ; $\hat{C} = 53^{0} 8'$

C. BC = 25; $\hat{B} = 36^{0} 52'$ ; $\hat{C} = 53^{0} 8'$

D. BC = 25; $\hat{B} = 36^{0} 52'$ ; $\hat{C} = 53^{0} 8'$

30. Nhiều lựa chọn

Cho tam giác ABC vuông tại A, AB = 6cm, AC = 4,5cm

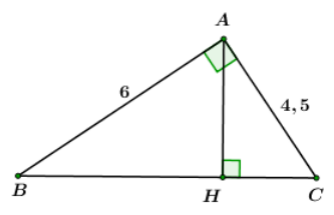
Cho tam giác ABC vuông tại A, AB = 6cm, AC = 4,5cm Tính các góc B, C và đường cao AH của tam giác? (ảnh 1)

Tính các góc B, C và đường cao AH của tam giác?

A. $\hat{B} = 53^{0} 8'$ ; $\hat{C} = 36^{0} 52'$ ; AH = 3,6cm

B. $\hat{B} = 36^{0} 52'$ ; $\hat{C} = 53^{0} 8'$ ; AH = 3,6cm

C. $\hat{B} = 48^{0} 35'$ ; $\hat{C} = 41^{0} 25'$ ; AH = 3,6cm

D. $\hat{B} = 41^{0} 25'$ ; $\hat{C} = 48^{0} 35'$ ; AH = 3,6cm

31. Nhiều lựa chọn

Cho tam giác ABC vuông tại A, $\hat{B} = 35^{0}$ và AB = 6cm. Vẽ đường cao AH và trung tuyến AM của tam giác ABC

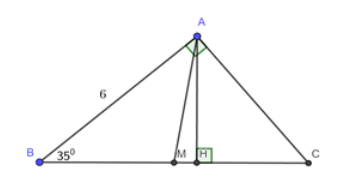
Cho tam giác ABC vuông tại A, góc = 35 độ và AB = 6cm Vẽ đường cao AH và trung tuyến AM (ảnh 1)

Giải tam giác ABC.

A. AC = 8,57cm; BC = 10,46cm; $\hat{C} = 55^{0}$ .

B. AC = 4,9cm; BC = 7,75cm; $\hat{C} = 55^{0}$ .

C. AC = 4,2cm; BC = 7,32cm; $\hat{C} = 55^{0}$ .

D. AC = 3,44cm; BC = 6,92cm; $\hat{C} = 55^{0}$ .

32. Nhiều lựa chọn

Cho $∆$ ABC vuông tại A có đường cao AH và đường trung tuyến AM. Biết AH = 3cm; HB = 4cm. Hãy tính AB, AC, AM và diện tích tam giác ABC.

A. AB = 5cm, AC = $\frac{15}{4}$ cm; AM = $\frac{25}{8}$ cm; $S_{∆ A B C} = \frac{75}{8} c m^{2}$ .

B. AB = 5cm, AC = 3cm; AM = 4cm; $S_{∆ A B C} = \frac{39}{4} c m^{2}$ .

C. AB = $\frac{14}{3}$ cm, AC = $\frac{14}{4}$ cm; AM = 3cm; $S_{∆ A B C} = \frac{75}{8} c m^{2}$ .

D. AB = $\frac{14}{3}$ cm, AC = 3 cm; AM = $\frac{27}{8}$ cm; $S_{∆ A B C} = 9 c m^{2}$

33. Nhiều lựa chọn

Cho tam giác ABC có AB = 4cm, AC = $4 \sqrt{3}$ , BC = 8cm.Tính số đo $\hat{B}$ , $\hat{C}$ và độ dài đường cao AH của ABC

A. $\hat{B} = 45^{0}$ ; $\hat{C} = 45^{0}$ ; AH = $\sqrt{3}$

B. $\hat{B} = 50^{0}$ ; $\hat{C} = 40^{0}$ ; AH = 2

C. $\hat{B} = 30^{0}$ ; $\hat{C} = 60^{0}$ ; AH = 4

D. $\hat{B} = 60^{0}$ ; $\hat{C} = 30^{0}$ ; AH = 2

34. Nhiều lựa chọn

Cho $∆$ MNP vuông tại M có đường cao MH. Gọi I, K lần lượt là hình chiếu vuông góc của H trên MN, MP. Biết HK = 9cm, HI = 6cm. Khi đó tính độ dài các cạnh của MNP.

A. MN = 12cm; MP = 19,5cm, NP = $\frac{3 \sqrt{13}}{2}$ cm

B. MN = 13cm; MP = 19,5cm, NP = $\frac{3 \sqrt{13}}{2}$ cm

C. MN = 13cm; MP = 17,5cm, NP = $\frac{3 \sqrt{13}}{2}$ cm

D. MN = 13cm; MP = 19,5cm, NP = $\frac{5 \sqrt{13}}{2}$ cm

Gợi ý cho bạn

QuizToán - Tốt nghiệp THPT

Trắc nghiệm củng cố

2 câu hỏi3 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi5 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi28 lượt thi

QuizToán - Lớp 12

10 bài tập Xác định các yếu tố cơ bản của đường thẳng trong không gian có lời giải

10 câu hỏi16 lượt thi

QuizToán - Lớp 12

10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải

10 câu hỏi14 lượt thi

QuizToán - Lớp 12

10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Khoảng cách từ một điểm đến một mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình mặt phẳng đi qua 1 điểm kèm điều kiện song song với mặt phẳng khác có lời giải

10 câu hỏi13 lượt thi

Facebook Youtube