138 CÂU HỎI
Mệnh đề nào đúng trong các mệnh đề sau?
A. Góc giữa hai đường thẳng bằng góc giữa hai vectơ chỉ phương của hai đường thẳng đó.
B. Góc giữa hai đường thẳng là góc nhọn.
C. Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c khi b song song với c (hoặc b trùng với c ).
D. Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c thì b song song với c .
Mệnh đề nào đúng trong các mệnh đề sau?
A. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho.
B. Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng b và mặt phẳng (P) khi a và b song song (hoặc a trùng với b ).
C. Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng a và mặt phẳng (Q) thì mặt phẳng (P) song song với mặt phẳng (Q) .
D. Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng b và mặt phẳng (P) thì a và b song song.
Mệnh đề nào đúng trong các mệnh đề sau?
A. Góc giữa hai mặt phẳng luôn là góc nhọn.
B. Góc giữa mặt phẳng (P) và mặt phẳng (Q) bằng góc giữa mặt phẳng (P) và mặt phẳng (R) khi mặt phẳng (R) song song với mặt phẳng (Q) (hoặc (R) trùng với (Q) ).
C. Góc giữa mặt phẳng (P) và mặt phẳng (Q) bằng góc giữa mặt phẳng (P) và mặt phẳng (R) thì mặt phẳng (R) song song với mặt phẳng (Q) .
D. Cả ba mệnh đề trên đều đúng.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , đường thẳng SA vuông góc với mặt phẳng đáy, SA = a . Góc giữa mặt phẳng (SCD) và mặt phẳng (ABCD) là . Khi đó nhận giá trị nào trong các giá trị sau:
A.
B.
C.
D.
Cho hình lập phương ABCD.A'B'C'D' . Xét mặt phẳng (A'BD), trong các mệnh đề sau, mệnh đề nào đúng?
A. Góc giữa mặt phẳng (A'BD) và các mặt phẳng chứa các mặt của hình lập phương bằng nhau.
B. Góc giữa mặt phẳng (A'BD) và các mặt phẳng chứa các mặt của hình lập phương bằng nhau.
C. Góc giữa mặt phẳng (A'BD) và các mặt phẳng chứa các mặt của hình lập phương bằng mà
D. Cả ba mệnh đề trên đều sai.
Cho hình chóp tứ giác S.ABCD có đáy là hình vuông và có một mặt bên vuông góc với đáy. Xét bốn mặt phẳng chứa bốn mặt bên và mặt phẳng chứa mặt đáy. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Có hai cặp mặt phẳng vuông góc nhau.
B. Có ba cặp mặt phẳng vuông góc nhau.
C. Có bốn cặp mặt phẳng vuông góc nhau.
D. Có năm cặp mặt phẳng vuông góc nhau.
Cho hình lập phương ABCD.EFGH, hãy xác định góc giữa cặp vectơ ?
A. 45o
B. 90o
C. 120o
D. 60o
Trong không gian cho ba đường thẳng phân biệt a, b, c. Mệnh đề nào sau đây đúng?
A. Nếu a và b cùng vuông góc với thì a // b .
B. Nếu a // b , thì
C. Nếu góc giữa a và c bằng góc giữa b và c thì a // b
D. Nếu a và b cùng nằm trong mặt phẳng và thì góc giữa a và c bằng góc giữa b và c .
Cho hình chóp S.ABC có . Hãy xác định góc giữa SB và AC.
A. 60o
B. 120o
C. 45o
D. 90o
Cho tứ diện ABCD có hai mặt ABC, ABD là các tam giác đều. Góc giữa AB và CD là
A. 120o
B. 60o
C. 90o
D. 30o
Cho hình hộp ABCD.A'B'C'D' . Giả sử tam giác AB'C, A'DC' là các tam giác nhọn. Góc giữa hai đường thẳng AC và A'D là góc nào sau đây?
A.
B.
C.
D.
Trong các mện đề sau, mệnh đề nào đúng?
A. Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì cũng vuông góc với đường thẳng thứ hai.
B. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
C. Hai đường thẳng phân biệt vuông góc với nhau thì chúng cắt nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.
Cho tứ diện ABCD. Gọi I, J, K lần lượt là trung điểm của BC, CA và BD. Khi đó góc giữa AB và CD là:
A.
B.
C.
D.
Cho một hình thoi ABCD cạnh a và một điểm S nằm ngoài mặt phẳng chứa hình thoi sao cho SA = a và vuông góc với (ABC). Tính góc giữa SD và BC
A. 60o
B. 90o
C. 45o
D.
Cho tứ diện ABCD. Gọi M, N, I lần lượt là trung điểm của BC, AD và AC. Cho AB = 2a, CD = và MN = . Tính góc
A. 135o
B. 60o
C. 90o
D. 45o
Cho hình chóp S.ABC có , SA = a, tam giác ABC đều cạnh a. Tính góc giữa SB và (ABC)
A.
B. 60o
C. 45o
D. 90o
Cho hình chóp S.ABC có , SA = a, tam giác ABC đều cạnh a . Tính ?
A.
B.
C.
D.
Cho tứ diện đều ABCD cạnh a. Gọi là góc giữa hai mặt phẳng (ABC) và (DBC). Tính ?
A. 3
B.
C.
D.
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a; và SA = a. Tính góc giữa hai mặt phẳng (ABCD) và (SBC)?
A.
B.
C.
D.
Cho hình chóp S.ABCD có cạnh đáy bằng a; và SA = a. Tính góc giữa hai mặt phẳng (SBC) và (SDC)?
A.
B.
C.
D.
Cho ba tia Ox, Oy, Oz trong không gian sao cho , , . Trên ba tia ấy lần lượt lấy các điểm A, B, C sao cho OA = OB = OC = a. Gọi lần lượt là góc giữa mặt phẳng (ABC) với mặt phẳng (OBC) và mặt phẳng (OAC). Tính ?
A.
B.
C.
D. 1
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a; và . Tính góc giữa hai đường thẳng SD và BC.
A. 60o
B. 30o
C. 45o
D. 90o
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a; và . Gọi I và J lần lượt là trung điểm của SA và SC . Tính góc giữa hai đường thẳng IJ và BD
A. 90o
B. 60o
C.
D. 45o
Cho tứ diện ABCD có . Gọi I, J, K lần lượt là trung điểm của BC, AC, DB. Biết .Tính góc giữa hai đường thẳng CD và IJ
A. 90o
B. 60o
C. 45o
D. 30o
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi M, N lần lượt là trung điểm của AB, BC. Tính góc giữa hai đường thẳng MN và C'D'
A. 90o
B. 45o
C. 60o
D. 30o
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Tính góc giữa hai đường thẳng BD và AD'
A. 90o
B. 45o
C. 60o
D. 30o
Cho hình lập phương ABCD.A'B'C'D' cạnh a . Gọi M, N, P lần lượt là trung điểm của AB, BC, C'D'. Tính góc giữa hai đường thẳng MN và AP
A. 90o
B. 45o
C. 60o
D. 30o
Cho hình lập phương ABCD.A'B'C'D' cạnh a . Gọi M, N, P lần lượt là trung điểm của AB, BC, C'D'. Tính góc giữa hai đường thẳng DN và A'P
A. 90o
B. 45o
C. 60o
D. 30o
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; và . Tính cosin góc tạo bởi SC và mặt phẳng (SAB)
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với (ABCD) cà . Tính sin của góc tạo bởi AC và mặt phẳng (SBC)
A.
B.
C.
D.
Cho lăng trụ đứng ABC.A'B'C'có đáy ABC cân đỉnh A, , BC' tạo đáy góc . Gọi I là trung điểm của AA', biết . Tính
A.
B. 2
C.
D. 1
Cho hình chóp S.ABC có SA là đường cao và đáy là tam giác ABC vuông tại B. Cho , gọi . Tìm để góc giữa hai mặt phẳng (ASC) và (BSC) bằng 60o
A.
B.
C.
D.
Cho mặt phẳng (P) và hai điểm A, B không nằm trong (P). Đặt và . Trong các kết luận sau thì kết luận nào đúng?
A. khi và chỉ khi AB // (P)
B. khi và chỉ khi đoạn thẳng AB cắt (P)
C. khi đoạn thẳng AB cắt (P)
D. Nếu đường thẳng AB cắt (P) tại điểm I thì
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc. Giả sử AB = 1, AC = 2, AD = 3. Khi đó khoảng cách từ A đến mặt phẳng (BCD) bằng:
A.
B.
C.
D.
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AD = b, AA' = c. Khoảng cách giữa hai đường thẳng BB' và AC' là:
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo a khoảng cách từ A đến mặt phẳng (SCD)
A.
B.
C.
D.
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Tìm mệnh đề đúng trong các mệnh đề sau?
A. Khoảng cách từ A đến mặt phẳng (A'BD) bằng
B. Độ dài
C. Khoảng cách từ A đến mặt phẳng (CDD'C') bằng
D. Khoảng cách từ A đến mặt phẳng (BCC'B') bằng
Cho tứ diện đều ABCD cạnh a. Gọi A' là hình chiếu của A trên mặt phẳng (BCD). Độ dài cạnh AA' là:
A.
B.
C.
D.
Cho tứ diện ABCD có AC = a, BD = 3a. Gọi M, N lần lượt là trung điểm của AD và BC. Biết . Tính MN
A.
B.
C.
D.
Cho hình lập phương ABCD.EFGH có cạnh a. Tính tích AB.EG?
A.
B.
C.
D.
Cho tứ diện ABCD có AB = 6, CD = 3. Góc giữa AB và CD bằng . Điểm M nằm trên đoạn BC sao cho BM = 2MC. Mặt phẳng (P) qua M song song với AB và CD cắt AC, AD và BD lần lượt tại N, P, Q. Tính diện tích MNPQ?
A.
B.
C.
D.
Cho tứ diện ABCD có , AB = CD = 6, .là điểm thuộc cạnh BC sao cho MC = xBC (0 < x < 1) Mặt phẳng (P) song song với AB và CD lần lượt cắt BC, AC, AD, BD tại M, N, P, Q. Diện tích lớn nhất của tứ giác MNPQ là:
A. 9
B. 6
C. 10
D. 12
Cho tứ diện ABCD có , AC = AD = 4, AB = 3, CD = 5. Tính khoảng cách từ A đến mặt phẳng (BCD)
A.
B.
C.
D.
Cho hình chóp S.ABC có , SA = 3a, AB = BC = 2a, . Tính khoảng cách từ A đến (SBC)
A.
B.
C.
D.
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, và SA = a. Tính khoảng cách từ A đến (SBC) theo a
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = a, CD = 2a, cạnh SD vuông góc với (ABCD), SD = a. Tính
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, , SA = a. Tính khoảng cách từ trung điểm I của SC đến (SBD).
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng , SA = a. Tính khoảng cách giữa hai đường thẳng SB và CD.
A. a
B.
C.
D. 2a
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng , SA = a. Gọi M là trung điểm của CD. Khoảng cách từ M đến (SAB) nhận giá trị nào sau đây?
A.
B. a
C.
D. 2a
Cho hình chóp S.ABC trong đó SA, AB, BC đôi một vuông góc và SA = AB = BC = 1. Tính độ dài SC
A.
B.
C. 2
D.
Cho tứ diện ABCD có DA = DB = DC và . Trong các mặt của tứ diện đó:
A. Tam giác ABD có diện tích lớn nhất.
B. Tam giác ACD có diện tích lớn nhất.
C. Tam giác BCD có diện tích lớn nhất.
D. Tam giác ABC có diện tích lớn nhất.
Cho tứ diện ABCD có hai cặp cạnh đối diện vuông góc. Cắt tứ diện đó bằng một mặt phẳng song song với một cặp cạnh đối diện còn lại của tứ diện. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Thiết diện là hình thang.
B. Thiết diện là hình bình hành.
C. Thiết diện là hình chữ nhật.
D. Thiết diện là hình vuông.
Cho hình chóp có đáy ABCD là hình vuông cạnh a, , . Tính khoảng cách từ A đến mặt phẳng (SBC)
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là nữa lục giác đều với đáy lớn AD = 2a, và . Tính khoảng cách từ A đến (SBC)
A.
B.
C.
D.
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau. Gọi a, b, c tương ứng là độ dài của các cạnh OA, OB, OC. Gọi h là khoảng cách từ O đến (ABC) thì h có giá trị là:
A.
B.
C.
D.
Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm O, cạnh a, đường chéo AC = a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy; góc giữa SC và (ABCD) bằng 60o . Gọi I là trung điểm của AB. Tính khoảng cách từ I đến (SBC).
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a, CD = a; góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 60o. Gọi I là trung điểm của AD, hai mặt phẳng (SBI) và (SCI) cùng vuông góc với (ABCD). Tính theo a khoảng cách từ A đến (SBC).
A.
B.
C.
D.
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Tìm giá trị của k thích hợp đẻ điền vào đẳng thức vectơ :
A.
B.
C.
D.
Cho ba vectơ . Điều kiện nào sau đây khẳng định đồng phẳng?
A. Tồn tại ba số thực m, n, p thoả mãn và
B. Tồn tại ba số thực m, n, p thoả mãn và
C. Tồn tại ba số thực m, n, p thoả mãn
D. Giá của đồng quy.
Cho lăng trụ tam giác ABC.A'B'C'D có . Hãy phân tích ( biểu thị) vectơ qua các vectơ .
A.
B.
C.
D.
Trong các mệnh đề sau đây, mệnh đề nào là đúng?
A. Nếu thì B là trung điểm của đoạn AC
B. Từ ta suy ra
C. Vì nên bốn điểm cùng thuộc một mặt phẳng.
D. Từ ta suy ra
Hãy chọn mệnh đề sai trong các mệnh đề sau đây:
A. Ba vectơ đồng phẳng nếu có hai trong ba vectơ đó cùng phương
B. Ba vectơ đồng phẳng nếu có một trong ba vectơ đó bằng vectơ
C. Vectơ luôn luôn đồng phẳng với hai vectơ và
D. Cho hình hộp ABCD.A'B'C'D' ba vectơ đồng phẳng.
Trong các kết luận sau đây, kết luận nào đúng?
Cho hình lập phương ABCD.EFGH có cạnh a. Ta có bằng:
A.
B.
C.
D.
Cho hình chóp S.ABCD. Gọi O là giao điểm của AC và BD. Trong các khẳng định sau, khẳng định nào sai?
A. Nếu thì ABCD là hình thang.
B. Nếu ABCD là hình bình hành thì
C. Nếu ABCD là hình thang thì
D. Nếu thì ABCD là hình bình hành.
Trong các mệnh đề sau đây, mệnh đề nào là sai?
A. Từ hệ thức ta suy ra ba vectơ đồng phẳng.
B. Vì nên N là đoạn trung điểm của đoạn MP
C. Vì I là trung điểm của đoạn AB nên từ một điểm O bất kì ta có
D. Vì nên bốn điểm cùng thuộc một mặt phẳng.
Cho hình hộp ABCD.A'B'C'D' có tâm O. Đặt . M là điểm xác định bởi . Khẳng định nào sau đây đúng?
A. M là trung điểm của BB'
B. M là tâm hình bình hành BCC'B'
C. M là tâm hình bình hành ABB'A'
D. M là trung điểm của CC'
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữ cặp vectơ và ?
A. 45°
B. 90°
C. 120°
D. 60°
Trong không gian cho hai hình vuông ABCD và A'B'C'D' có cạnh chung AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm O và O'. Hãy xác định góc giữa cặp vectơ và ?
A. 60°
B. 45°
C. 120°
D. 90°
Cho hình chóp S.ABC có SA = SB = SC và . Hãy xác định góc giữa cặp vectơ và ?
A. 60°
B. 120°
C. 45°
D. 90°
Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Góc giữa AB và CD là?
A. 120°
B. 60°
C. 90°
D. 30°
Cho hình chóp S.ABCD có tất cả các cạch đều bằng A. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc (IJ, CD) bằng:
A. 90°
B. 45°
C. 30°
D. 60°
Cho hình hộp ABCD.A'B'C'D'. Giả sử tam giác AB'C và A'DC' đều có 3 góc nhọn. Góc giữa hai đường thẳng AC và A'D là góc nào sau đây?
A.
B.
C.
D.
Trong các mệnh đề dưới đây mệnh đề đúng là?
A. Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì cũng vuông góc với đường thẳng thứ hai.
B. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
C. Hai đường thẳng phân biệt vuông góc với nhau thì chúng cắt nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.
Cho hình chóp S.ABC có SA = SB = SC và . Hãy xác định góc giữa cặp vectơ và ?
A. 120°
B. 45°
C. 60°
D. 90°
Cho hình chóp S.ABC có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo của góc (MN, SC) bằng:
A. 45°
B. 30°
C. 90°
D. 60°
Cho hình lập phương ABCD.A1B1C1D1. Chọn khẳng định sai?
A. Góc giữa AC và B1D1 bằng 90o
B. Góc giữa B1D1 và AA1 bằng 60o
C. Góc giữa AD và B1C bằng 45o
D. Góc giữa BD và A1C1 bằng 90o
Cho hình lập phương 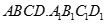 có cạnh a. Gọi M là trung điểm AD. Giá trị
có cạnh a. Gọi M là trung điểm AD. Giá trị 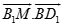 là:
là:
A. 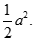
C. 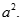
C. 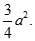
D. 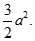
Trong các mệnh đề sau đây, mệnh đề nào là đúng?
A. Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b vuông góc với đường thẳng b thì a vuông góc với c
B. Cho ba đường thẳng a, b, c vuông góc với nhau từng đôi một. Nếu có một đường thẳng d vuông góc với a thì d song song với b hoặc c
C. Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b song song với đường thẳng c thì a vuông góc với c
D. Cho hai đường thẳng a và b song song với nhau. Một đường thẳng c vuông góc với a thì c vuông góc với mọi đường thẳng nằm trong mặt phẳng (a, b)
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ và ?
A. 90°
B. 60°
C. 45°
D. 120°
Cho tứ diện ABCD đều cạnh bằng a. Gọi M là trung điểm của CD, là góc giữa AC và BM. Chọn khẳng định đúng?
A. 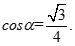
B. 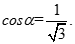
C. 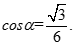
D. 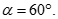
Cho 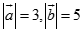 góc giữa
góc giữa 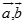 bằng
bằng 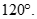 Chọn khẳng định sai trong các khẳng định sau?
Chọn khẳng định sai trong các khẳng định sau?
A. 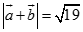
B. 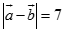
C. 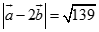
D. 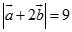
Cho hình lập phương 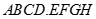 . Hãy xác định góc giữa cặp vectơ
. Hãy xác định góc giữa cặp vectơ 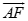 và
và 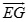 ?
?
A. 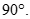
B. 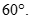
C. 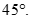
D. 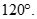
Trong không gian cho ba điểm A, B, C bất kỳ, chọn đẳng thức đúng?
A. 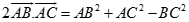
B. 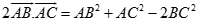
C. 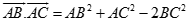
D. 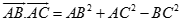
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính 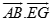
A. 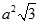
B. 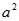
C. 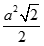
D. 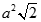
Cho tứ diện ABCD có AB vuông góc với CD, AB = CD = 6. M là điểm thuộc BC sao cho MC = x.BC (0 < x < 1). Mặt phẳng (P) song song với AB và CD lần lượt cắt BC, DB, AD, AC tại M, N, P, Q. Diện tích lớn nhất của tứ giác bằng bao nhiêu?
A. 9
B. 11
C. 10
D. 8
Cho tứ diện ABCD có AB = CD. Gọi I, J, E, F lần lượt là trung điểm của AC, BC, BD, DA. Góc giữa IE và JF là:
A. 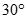
B. 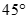
C. 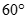
D. 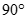
Mệnh đề nào sau đây là đúng?
A. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.
B. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
Cho hai vec tơ 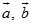 thỏa mãn
thỏa mãn 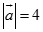 ,
, 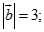
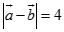 . Gọi là góc giữa hai véc tơ và . Chọn khẳng định đúng:
. Gọi là góc giữa hai véc tơ và . Chọn khẳng định đúng:
A. 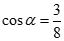
B. 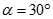
C. 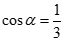
D. 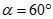
Cho tứ diện ABCD. Tìm giá trị của k thích hợp thỏa mãn: 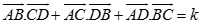
A. k = 1
B. k = 2
C. k = 0
D. k = 4
Trong không gian cho tam giác ABC. Tìm điểm M sao cho giá trị của biểu thức 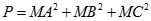 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
A. M là trọng tâm tam giác ABC
B. M là tâm đường tròn ngoại tiếp tam giác ABC
C. M là trực tâm tam giác ABC
D. M là tâm đường tròn nội tiếp tam giác ABC
Cho hai vec tơ 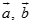 thỏa mãn
thỏa mãn 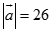 ;
; 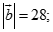
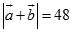 . Độ dài của vec tơ
. Độ dài của vec tơ 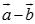 là:
là:
A. 25
B. 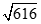
C. 9
D. 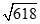
Cho hai vec tơ 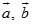 thỏa mãn
thỏa mãn 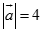 ;
; 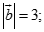
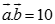 . Xét hai véc tơ
. Xét hai véc tơ 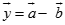 ;
; 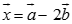 . Gọi là góc giữa hai véc tơ và . Chọn khẳng định đúng:
. Gọi là góc giữa hai véc tơ và . Chọn khẳng định đúng:
A. 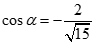
B. 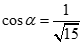
C. 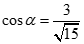
D. 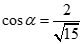
Trong không gian cho tam giác ABC có diện tích S. Tìm giá trị của k thích hợp thỏa mãn: 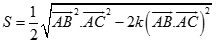
A. k =
B. k = 0
C. k =
D. k = 1
Trong không gian cho đường thẳng d và điểm O. Qua O có bao nhiêu đường thẳng vuông góc với d
A. Vô số
B. 2
C. 3
D. 1
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và SA = SB = SC = b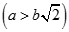 . Gọi G là trọng tâm tam giác ABC. Xét mặt phẳng (P) đi qua A và vuông góc với SC tại điểm I nằm giữa S và C. Diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P) là:
. Gọi G là trọng tâm tam giác ABC. Xét mặt phẳng (P) đi qua A và vuông góc với SC tại điểm I nằm giữa S và C. Diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P) là:
A. 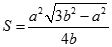
B. 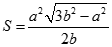
C. 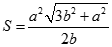
D. 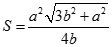
Cho tứ diện ABCD có cạnh AB, BC, BD vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng:
A. Góc giữa CD và (ABD) là góc
B. Góc giữa AC và (CBD) là góc
C. Góc giữa AD và (ABC) là góc
D. Góc giữa AC và (ABD) là góc
Cho hình chóp S.ABC có SA = SB = SC và tam giác ABC vuông tại B. Vẽ 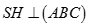 ,
, 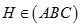 . Khẳng định nào sau đây đúng:
. Khẳng định nào sau đây đúng:
A. H trùng với trung điểm của AC
B. H là trọng tâm tam giác ABC
C. H là trực tâm tam giác ABC
D. H trùng với trung điểm của BC
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S lên mặt phẳng (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và mặt phẳng (ABC)
A. 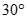
B. 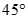
C. 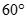
D. 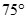
Mệnh đề nào sau đây là sai?
A. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.
C. Một đường thẳng và một mặt phẳng (không chứa đường thẳng đã cho ) cùng vuông góc với một đường thẳng thì song song với nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
Cho hình chóp S.ABC có SA = SB = SC, , . Vẽ 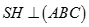 ,
, 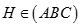 . Khẳng định nào sau đây đúng:
. Khẳng định nào sau đây đúng:
A. H trùng với trung điểm của AB
B. H là trọng tâm tam giác ABC
C. H trùng với trung điểm của BC
D. H trùng với trung điểm của AC
Cho hình chóp S.ABCD có đáy là hình thoi tâm O và . Khẳng định nào sau đây sai:
A. 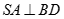
B. 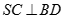
C. 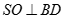
D. 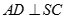
Cho hình chóp S.ABC có đáy là tam giác đều, O là trung điểm của đường cao AH của tam giác ABC và 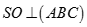 . Gọi I là điểm tùy ý trên OH ( không trùng với O và H). Xét mặt phẳng (P) đi qua I và vuông góc với OH. Thiết diện của hình chóp cắt bởi mặt phẳng (P) là:
. Gọi I là điểm tùy ý trên OH ( không trùng với O và H). Xét mặt phẳng (P) đi qua I và vuông góc với OH. Thiết diện của hình chóp cắt bởi mặt phẳng (P) là:
A. Hình thang cân.
B. Hình thang vuông.
C. Hình bình hành.
D. Tam giác vuông.
Cho hình chóp S.ABCD có đáy là hình vuông tâm O và 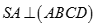 . Gọi I là trung điểm của SC. Khẳng định nào sau đây sai:
. Gọi I là trung điểm của SC. Khẳng định nào sau đây sai:
A. 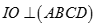
B. 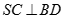
C. SA = SB = SC
D. (SAC) là mặt phẳng trung trực của BD
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, 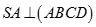 và
và 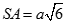 . Gọi là góc giữa SC và (ABCD). Chọn khẳng định đúng:
. Gọi là góc giữa SC và (ABCD). Chọn khẳng định đúng:
A. 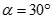
B. 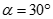
C.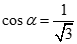
D. 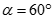
Cho hình chóp S.ABC có các mặt bên tạo với đáy một góc bằng nhau. Hình chiếu H của S lên mặt phẳng (ABC) là:
A. Trọng tâm tam giác ABC
B. Tâm đường tròn ngoại tiếp tam giác ABC
C. Trực tâm tam giác ABC
D. Tâm đường tròn nội tiếp tam giác ABC
Cho a, b, c là các đường thẳng trong không gian. Mệnh đề nào sau đây là sai?
A. Nếu 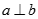 và
và 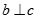 thì a // b
thì a // b
B. Nếu 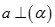 và
và 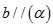 thì
thì 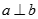
C. Nếu a // b và 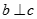 thì
thì 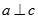
D. Nếu 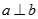 ,
, 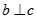 và a cắt c thì b vuông góc với mặt phẳng chứa a và c.
và a cắt c thì b vuông góc với mặt phẳng chứa a và c.
Cho hình chóp S.ABC có 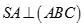 và
và 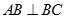 . Số các mặt của hình chóp S.ABC là tam giác vuông là
. Số các mặt của hình chóp S.ABC là tam giác vuông là
A. 1
B. 2
C. 3
D. 4
Cho hình chóp S.ABCD có đáy là hình chữ nhật, 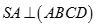 . Gọi AE, AF lần lượt là các đường cao của tam giác SAB và SAD. Khẳng định nào sau đây đúng:
. Gọi AE, AF lần lượt là các đường cao của tam giác SAB và SAD. Khẳng định nào sau đây đúng:
A. 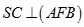
B. 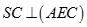
C. 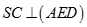
D. 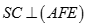
Cho hình hộp ABCD.A'B'C'D' có đáy là hình thoi, và A'A = A'B = A'D. Gọi O là giao điểm của AC và BD. Hình chiếu của A' lên mặt phẳng (ABCD) là:
A. Trung điểm của AO
B. Trọng tâm tam giác ABD
C. Điểm O
D. Trọng tâm tam giác BCD
Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và 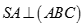 ,
, 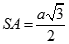 . Xét mặt phẳng (P) đi qua A và vuông góc với BC. Diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P) là:
. Xét mặt phẳng (P) đi qua A và vuông góc với BC. Diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P) là:
A. 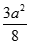
B. 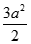
C. 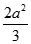
D. 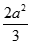
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, 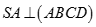 và
và 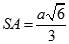 . Gọi
. Gọi 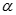 là góc giữa SC và (ABCD). Chọn khẳng định đúng:
là góc giữa SC và (ABCD). Chọn khẳng định đúng:
A. 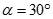
B. 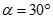
C. 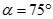
D. 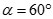
Cho hình lập phương ABCD.A'B'C'D'. Gọi 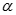 là góc giữa AC' và (A'BCD'). Chọn khẳng định đúng:
là góc giữa AC' và (A'BCD'). Chọn khẳng định đúng:
A. 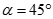
B. 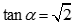
C. 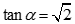
D. 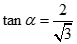
Cho tứ diện S.ABC thỏa mãn SA = SB = SC. Gọi H là hình chiếu vuông góc của S lên mặt phẳng (ABC). Đối với tam giác ABC ta có điểm H là
A. Trực tâm.
B. Tâm đường tròn nội tiếp.
C. Trọng tâm.
D. Tâm đường tròn ngoại tiếp.
Cho tứ diện ABCD có hai mặt (ABC) và (SBC) là hai tam giác đều cạnh a, 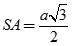 . M là điểm trên AB sao cho AM = b (0 < b < a). (P) là mặt phẳng qua M và vuông góc với BC. Thiết diện của (P) và tứ diện SABC có diện tích bằng?
. M là điểm trên AB sao cho AM = b (0 < b < a). (P) là mặt phẳng qua M và vuông góc với BC. Thiết diện của (P) và tứ diện SABC có diện tích bằng?
A. 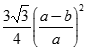
B. 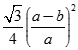
C. 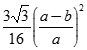
D. 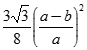
Cho hai đường thẳng a, b và mặt phẳng (P). Chỉ ra mệnh đề đúng trong các mệnh đề sau:
A. Nếu a // (P) và 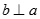 thì b // (P)
thì b // (P)
B. Nếu a // (P) và 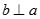 thì
thì 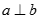
C. Nếu a // (P) và 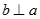 thì
thì 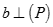
D. Nếu 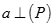 và
và 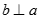 thì b // (P)
thì b // (P)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SA = a. Tính số đo của góc giữa SA và mặt phẳng (ABC).
A. 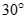
B. 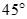
C. 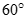
D. 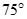
Tính chất nào sau đây không phải tính chất của hình lăng trụ đứng?
A. Các mặt bên của hình lăng trụ đứng là những hình bình hành
B. Các mặt bên của hình lăng trụ đứng là những hình chữ nhật.
C. Các cạnh bên của hình lăng trụ đứng song song và bằng nhau
D. Hai đáy của hình lăng trụ đứng có các cạnh đôi một song song và bằng nhau
Chỉ ra mệnh đề sai trong các mệnh đề sau:
A. Cho hai đường thẳng vuông góc với nhau, mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
B. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
C. Cho hai mặt phẳng song song, đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.
D. Cho hai đường thẳng song song, mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
Cho hình chóp S.ABDC có đáy ABDC là hình bình hành tâm O, AD, SA, AB đôi một vuông góc, AD = 8, SA = 6. (P) là mặt phẳng qua trung điểm của AB và vuông góc với AB. Thiết diện của (P) và hình chóp có diện tích bằng ?
A. 20
B. 16
C. 17
D. 36
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA = SB = SC = b. Gọi g là trọng tâm tam giác ABC . Độ dài SG bằng:
A. 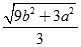
B. 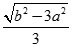
C. 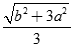
D. 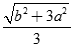
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA = SB = SC = b. Gọi G là trọng tâm tam giác ABC. Xét mặt phẳng (P) đi qua A và vuông góc với SC. Tìm hệ thức liên hệ giữa a và b để mặt phẳng (P) cắt SC tai điểm C1 nằm giữa S và C
A. 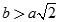
B. 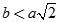
C. 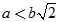
D. 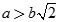
Cho hình chóp S.ABCD có đáy ABCD là hình thoi thoi tâm O. Biết SA = SC, SB = SD. Khẳng định nào sau đây đúng?
A. 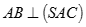
B. 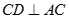
C. 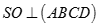
D. 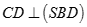
Cho tứ diện đều cạnh a = 12, AP là đường cao của tam giác ACD. Mặt phẳng (P) qua B vuông góc với AP cắt mặt phẳng (ACD) theo đoạn giao tuyến có độ dài bằng:
A. 9
B. 6
C. 8
D. 7
Tam giác ABC có BC = 2a, đường cao 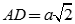 . Trên đường thẳng vuông góc với (ABC) tại A, lấy điểm S sao cho
. Trên đường thẳng vuông góc với (ABC) tại A, lấy điểm S sao cho 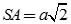 . Gọi E, F lần lượt là trung điểm của SB, SC. Diện tích tam giác AEF bằng?
. Gọi E, F lần lượt là trung điểm của SB, SC. Diện tích tam giác AEF bằng?
A. 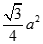
B. 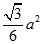
C. 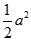
D. 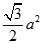
Cho hình lập phương 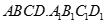 . Gọi
. Gọi 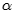 là góc giữa
là góc giữa 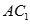 và mặt phẳng (ABCD). Chọn khẳng định đúng trong các khẳng định sau:
và mặt phẳng (ABCD). Chọn khẳng định đúng trong các khẳng định sau:
A. 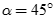
B. 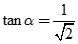
C. 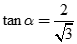
D. 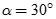
Cho hình lập phương ABCD.A'B'C'D'. Đường thẳng AC' vuông góc với mặt phẳng nào sau đây?
A. (A'BD)
C. (A'DC')
C. (A'CD')
D. (A'B'CD)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy, SA = a. Góc giữa đường thẳng SC và mặt phẳng (SAB) là a khi đó tan nhận giá trị nào trong các giá trị sau ?
A. 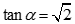
B. 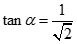
C. 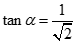
D. 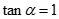
Cho hình chóp S.ABC có và tam giác ABC không vuông. Gọi H, K lần lượt là trực tâm của tam giác ABC và tam giác SBC. Số đo góc tạo bởi SC và (BHK) là:
A. 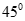
B. 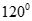
C. 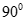
D. 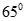
Cho hình vuông ABCD tâmO và cạnh bằng 2a. Trên đường thẳng qua O vuông góc với (ABCD) lấy điểm S. Biết góc giữa SA và mặt phẳng (ABCD) có số đo bằng 45o. Tính độ dài SO
A. 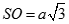
B. 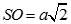
C. 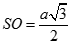
D. 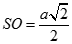
Cho hình chóp S.ABCD trong đó ABCD là hình chữ nhật, 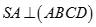 . Trong các tam giác sau tam giác nào không phải là tam giác vuông.
. Trong các tam giác sau tam giác nào không phải là tam giác vuông.
A. 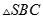
B. 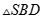
C. 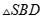
D. 
Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều tâm O, cạnh a, hình chiếu của C' trên mặt phẳng (ABC) trùng với tâm của đáy. Cạnh bên CC' hợp với mặt phẳng (ABC) góc 60o . Gọi I là trung điểm của AB. Tính khoảng cách từ C đến IC'
A.
Cho lăng trụ có đáy là tam giác đều tâm , cạnh hình chiếu của trên mặt phẳng trùng với tâm của đáy. Cạnh bên hợp với mặt phẳng góc Gọi là trung điểm của Tính khoảng cách từ đến
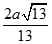
B. 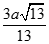
C. 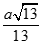
D. 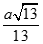
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Tính khoảng cách từ C đến AC'
A. 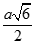
B. 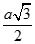
C. 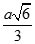
D. 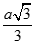
Cho hình chóp đều S.ABC có cạnh đáy bằng a. Gọi O là tâm của đáy và 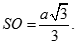 Tính khoảng cách từ O tới SA
Tính khoảng cách từ O tới SA
A. 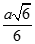
B. 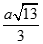
C. 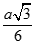
D. 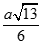
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy, SA = a. Góc giữa đường thẳng SD và mặt phẳng (SAC) bằng 30o , với M là trung điểm CD. Hãy tính khoảng cách từ D đến (SBM)
A. 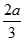
B. 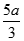
C. 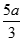
C. 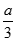
Cho hình chóp S.ABC có đáy là tam giác vuông tại A và 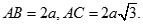 Hình chiếu vuông góc của S trên mặt phẳng (ABC) là trung điểm H của cạnh AB. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng 30o. Tính khoảng cách từ trung điểm M của cạnh BC đến mặt phẳng (SAC)
Hình chiếu vuông góc của S trên mặt phẳng (ABC) là trung điểm H của cạnh AB. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng 30o. Tính khoảng cách từ trung điểm M của cạnh BC đến mặt phẳng (SAC)
A. 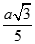
B. 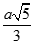
C. 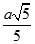
D. 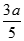
Cho lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a và 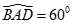 . Gọi O, O' lần lượt là tâm của hai đáy, gọi S là trung điểm của OO'. Tính khoảng cách từ O tới mặt phẳng (SAB) biết OO' = 2a
. Gọi O, O' lần lượt là tâm của hai đáy, gọi S là trung điểm của OO'. Tính khoảng cách từ O tới mặt phẳng (SAB) biết OO' = 2a
A. 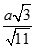
B. 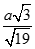
C. 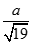
D. 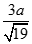
Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân, 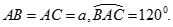 Mặt phẳng (AB'C') tạo với đáy góc 60o . Tính khoảng cách từ đường thẳng BC đến mặt phẳng (AB'C') theo a
Mặt phẳng (AB'C') tạo với đáy góc 60o . Tính khoảng cách từ đường thẳng BC đến mặt phẳng (AB'C') theo a
A. 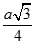
B. 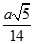
C. 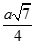
D. 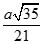
Cho hình lăng trụ ABC.A1B1C1 có các mặt bên là các hình vuông cạnh a. Gọi D, E, F lần lượt là trung điểm các cạnh BC, A1C1, B1C1. Tính theo a khoảng cách giữa hai đường thẳng DE và A1F
A. 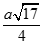
B. 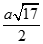
C. 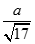
D.