(Trả lời ngắn) 29 bài tập Phương trình đường thẳng trong không gian (có lời giải)
29 câu hỏi
Trong không gian \[Oxyz\], cho hai đường thẳng: \({d_1}:\frac{x}{1} = \frac{y}{{ - 2}} = \frac{{z - 1}}{1}\), \({d_2}:\frac{{x - 1}}{2} = \frac{{y + 1}}{1} = \frac{{z - 1}}{1}\). Tìm tọa độ giao điểm của \({d_1}\) và \({d_2}\).
Trong không gian với hệ trục tọa độ\[Oxyz\], cho điểm \[H\left( {2;1;2} \right)\], \[H\] là hình chiếu vuông góc của gốc tọa độ \[O\] xuống mặt phẳng\[\left( P \right)\]. Tính số đo góc giữa mặt \[\left( P \right)\] và mặt phẳng \[\left( Q \right):x + y - 11 = 0\].
Trong không gian \[Oxyz\], cho mặt phẳng \[(P)\]có phương trình \[x - 2y + 2z - 5 = 0\]. Xét mặt phẳng \[(Q):x + (2m - 1)z + 7 = 0\], với \[m\]là tham số thực. Tìm tất cả giá trị của \[m\] để \[(P)\] tạo với \[(Q)\] góc \[\frac{\pi }{4}\].
Trong không gian với hệ trục tọa độ \(Oxyz\), lập phương trình tham số của đường thẳng \(d\) đi qua gốc tọa độ \(O\) và có vectơ chỉ phương \(\overrightarrow u = \left( {1\,;3\,;2} \right)\).
Trong không gian \(Oxyz\), cho ba điểm \[A\left( {1\,;\,0\,;\,1} \right)\], \(B\left( {1\,;\,1\,;\,0} \right)\) và \(C\left( {3\,;\,4\,;\, - 1} \right)\). Lập phương trình đường thẳng đi qua \(A\) và song song với \(BC\).
Trong không gian với hệ tọa độ \[Oxyz\], cho hai điểm \(A\left( {1; - 2; - 3} \right)\); \(B\left( { - 1;4;1} \right)\) và đường thẳng \(d:\frac{{x + 2}}{1} = \frac{{y - 2}}{{ - 1}} = \frac{{z + 3}}{2}\). Lập phương trình của đường thẳng đi qua trung điểm của đoạn \(AB\) và song song với \(d\)?
Trong không gian với hệ toạ độ \[Oxyz\], cho điểm \[A\left( {1; - 2;3} \right)\] và hai mặt phẳng \[\left( P \right):{\rm{ }}x + y + z + 1 = 0\], \[\left( Q \right):{\rm{ }}x - y + z - 2 = 0\]. Lập phương trình đường thẳng đi qua \[A\], song song với \[\left( P \right)\] và \[\left( Q \right)\]?
Trong không gian Oxyz, cho điểm \(M\left( {2;1; - 2} \right)\)và mặt phẳng \(\left( P \right):3x + 2y - z + 1 = 0.\) Lập phương trình đường thẳng đi qua M và vuông góc với \(\left( P \right)\).
Trong không gian \(Oxyz\), cho ba điểm B(1; 1; 2), C(1; -1; 0) và D(0; 0; 1). Lập phương trình đường thẳng đi qua \(B\) và vuông góc với mặt phẳng \(\left( {BCD} \right)\).
Trong không gian \[Oxyz,\] cho các điểm \(A\left( {1;0;2} \right),B\left( {1;2;1} \right),C\left( {3;2;0} \right)\) và \(D\left( {1;1;3} \right).\) Lập phương trình đường thẳng đi qua A và vuông góc với mặt phẳng \(\left( {BCD} \right)\).
Trong không gian \[Oxyz,\] lập hương trình đường thẳng \[\Delta \] là giao của hai mặt phẳng \[x + z - 5 = 0\] và \[x - 2y - z + 3 = 0\].
Trong không gian với hệ tọa độ \[Oxyz\], cho tam giác \[ABC\] có \[A\left( { - 1;3;2} \right),\,\,B\left( {2;0;5} \right),\,\,C\left( {0; - 2;1} \right)\]. Viết phương trình đường trung tuyến \[AM\] của tam giác \[ABC\].
Trong không gian Oxyz, cho điểm M(2; -2; 3) và đường thẳng : . Lập phương trình mặt phẳng đi qua điểm M và vuông góc với đường thẳng d.
Trong không gian Oxyz, lập phương trình mặt phẳng đi qua điểm A(0; 1; 0) và chứa đường thẳng .
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(-1; 3; 2) và đường thẳng d có phương trình . Lập phương trình mặt phẳng (P) chứa điểm A và vuông góc đường thẳng d.
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng \(\left( P \right)\) song song và cách đều hai đường thẳng \({d_1}:\frac{{x - 2}}{{ - 1}} = \frac{y}{1} = \frac{z}{1}\left( P \right):2y - 2z + 1 = 0\) và \({d_2}:\frac{x}{2} = \frac{{y - 1}}{{ - 1}} = \frac{{z - 2}}{{ - 1}}\).
Trong không gian \[Oxyz\], phương trình mặt phẳng chứa hai đường thẳng: \[\left( d \right):\left\{ \begin{array}{l}x = t + 2\\y = 3t - 1\\z = 2t + 1\end{array} \right.\] và \[\left( \Delta \right):\left\{ \begin{array}{l}x = m + 3\\y = 3m - 2\\z = 2m + 1\end{array} \right.\] có dạng \[x + ay + bz + c = 0\]. Tính \[P = a + 2b + 3c\].
Trong không gian \[Oxyz\], cho hai đường thẳng \[d:\frac{{x - 1}}{{ - 2}} = \frac{{y + 2}}{1} = \frac{{z - 4}}{3}\] và \[d':\left\{ {\begin{array}{*{20}{c}}{x = - 1 + t}\\{y = - t}\\{z = - 2 + 3t}\end{array}} \right.\]cắt nhau. Lập phương trình mặt phẳng chứa \[d\] và \[d'\].
Trong không gian với hệ tọa độ \(Oxyz,\) cho hai điểm \(A\left( {3;1;7} \right),\,B\left( {5;5;1} \right)\) và mặt phẳng \(\left( P \right):\,2x - y - z + 4 = 0\). Điểm \(M\) thuộc \(\left( P \right)\) sao cho \(MA = MB = \sqrt {35} .\) Biết \(M\) có hoành độ nguyên, tính \(OM\).
Trong không gian \[Oxyz\]cho ba đường thẳng \[d:\frac{x}{1} = \frac{y}{1} = \frac{{z + 1}}{{ - 2}},\]\[{\Delta _1}:\frac{{x - 3}}{2} = \frac{y}{1} = \frac{{z - 1}}{1},\]\[{\Delta _2}:\frac{{x - 1}}{1} = \frac{{y - 2}}{2} = \frac{z}{1}\]. Đường thẳng \[\Delta \]vuông góc với \[d\] đồng thời cắt \[{\Delta _1},{\Delta _2}\] tương ứng tại \[H,K\] sao cho độ dài \[HK\] nhỏ nhất. Biết rằng \[\Delta \] có một vectơ chỉ phương \[\overrightarrow u \left( {h;k;1} \right).\] Tính giá trị \[h - k\].
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {3\,;\,1\,;\,2} \right)\), \(B\left( { - 3\,;\, - 1\,;\,0} \right)\) và mặt phẳng \(\left( P \right):x + y + 3z - 14 = 0\). Điểm \(M\) thuộc mặt phẳng \(\left( P \right)\) sao cho \(\Delta MAB\) vuông tại \(M\). Tính khoảng cách từ điểm \(M\) đến mặt phẳng \(\left( {Oxy} \right)\).
Trong không gian với hệ tọa độ \(Oxyz\) cho đường thẳng \(d:\frac{{x - 5}}{2} = \frac{{y + 7}}{2} = \frac{{z - 12}}{{ - 1}}\) và mặt phẳng \(\left( \alpha \right):x + 2y - 3z - 3 = 0\). Gọi \(M\) là giao điểm của \(d\) và \(\left( \alpha \right)\), \(A\) thuộc \(d\) sao cho \(AM = \sqrt {14} \). Tính khoảng cách từ \(A\)đến mặt phẳng \(\left( \alpha \right)\).
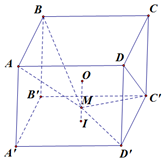
Cho hình lập phương \[ABCD.A'B'C'D'\] có tâm \(O\). Gọi \(I\) là tâm của hình vuông \(A'B'C'D'\) và điểm \(M\) thuộc đoạn \(OI\) sao cho \(MO = 2MI\) (tham khảo hình vẽ). Tính sin của góc tạo bởi hai mặt phẳng \(\left( {MC'D'} \right)\) và \(\left( {MAB} \right)\).
Cho hình lăng trụ \(ABC.A'B'C'\)có đáy \(ABC\) là tam giác vuông tại \(A\), \(AB = a\),\(AC = a\sqrt 3 \). Hình chiếu vuông góc của \(A'\) lên mặt phẳng \(\left( {ABC} \right)\) là trung điểm \(H\) của \(BC\), \(A'H = a\sqrt 5 \). Gọi \(\varphi \) là góc giữa hai đường thẳng \(A'B\) và \(B'C\). Tính \(\cos \varphi \).
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\), có \(AB = a,\,AD = a\sqrt 2 ,\)góc giữa \(A'C\)và mặt phẳng \(\left( {ABCD} \right)\) bằng \(30^\circ \). Gọi \(H\)là hình chiếu vuông góc của \(A\)trên \(A'B\)và \(K\) là hình chiếu vuông góc của \(A\) trên \(A'D.\) Tính góc giữa hai mặt phẳng\(\left( {AHK} \right)\) và \(\left( {ABB'A'} \right)\).
Cho hình lăng trụ đứng \[ABC.A'B'C'\]có \[AB = AC = a,{\rm{ }}BAC = 120^\circ \]. Gọi \[M,{\rm{ }}N\]lần lượt là trung điểm của \[B'C'\]và \[CC'\]. Biết thể tích khối lăng trụ \[ABC.A'B'C'\]bằng \[\frac{{\sqrt 3 {a^3}}}{4}\]. Gọi \[\alpha \]là góc giữa mặt phẳng \[\left( {AMN} \right)\]và mặt phẳng \[\left( {ABC} \right)\], tính \[\cos \alpha \].
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B\), \(AC = 2a\), tam giác \(SAB\) và tam giác \(SCB\) lần lượt vuông tại \(A\), \(C\). Khoảng cách từ \(S\) đến mặt phẳng \[\left( {ABC} \right)\] bằng \(2a\). Tính côsin của góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCB} \right)\),
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác cân đỉnh \(A\). Biết \(BC = a\sqrt 3 \) và , cạnh bên \(AA' = a\). Gọi \(M\) là điểm thỏa mãn \(2\overrightarrow {CM} = 3\overrightarrow {CC'} \). Gọi \(\alpha \) là góc tạo bởi hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {AB'M} \right)\), khi đó tính \(\sin \alpha \).
Cho khối tứ diện \(ABCD\) có \(BC = 3\), \(CD = 4\), . Góc giữa đường thẳng \(AD\) và \(BC\) bằng . Tính côsin góc giữa hai phẳng \(\left( {ABC} \right)\) và \(\left( {ACD} \right)\) .








