42 bài tập Góc giữa 2 đường thẳng, giữa đường thẳng và mặt phẳng, giữa hai mặt phẳng (có lời giải)

Tính góc giữa hai đường thẳng \(d\) và \({d^\prime }\) trong mỗi trường hợp sau:

a) \(d:\frac{{x - 1}}{1} = \frac{{y + 2}}{2} = \frac{{z - 1}}{1}\) và \({d^\prime }:\frac{{x - 1}}{1} = \frac{{y + 2}}{1} = \frac{{z - 1}}{2}\);

b) d: \(\frac{{x + 2}}{1} = \frac{{y + 4}}{2} = \frac{{z + 1}}{2}\) và \({d^\prime }:\left\{ {\begin{array}{*{20}{l}}{x = 2 - 2t}\\{y = 2 - 2t}\\{z = 1 + t}\end{array}} \right.\)

c) \(d:\left\{ {\begin{array}{*{20}{l}}{x = 1 + t}\\{y =  - 1 + 2t}\\{z =  - 2 - t}\end{array}} \right.\) và \({d^\prime }:\left\{ {\begin{array}{*{20}{l}}{x = 2 + 2{t^\prime }}\\{y = 3 + 4{t^\prime }}\\{z = 10{t^\prime }.}\end{array}} \right.\)

Tính góc giữa hai đường thẳng \(d\) và \({d^\prime }\) trong mỗi trường hợp sau:

a) d: \(\frac{{x - 7}}{3} = \frac{y}{5} = \frac{{z - 11}}{4}\) và \({d^\prime }:\frac{{x - 3}}{2} = \frac{{y + 6}}{5} = \frac{{z - 1}}{{ - 4}}\);

b) \(d:\frac{{x + 9}}{3} = \frac{{y + 4}}{6} = \frac{{z + 1}}{6}\) và \({d^\prime }:\left\{ {\begin{array}{*{20}{l}}{x = 9 - 10t}\\{y = 7 - 10t}\\{z = 15 + 5t}\end{array}} \right.\)

c) \(d:\left\{ {\begin{array}{*{20}{l}}{x = 23 + 2t}\\{y = 57 + t}\\{z = 19 - 5t}\end{array}} \right.\) và \({d^\prime }:\left\{ {\begin{array}{*{20}{l}}{x = 24 + {t^\prime }}\\{y = 6 + {t^\prime }}\\{z = {t^\prime }}\end{array}} \right.\)

Tính góc giữa đường thẳng \(d\) và mặt phẳng \((P)\) trong mỗi trường hợp sau:

a) \(d:\frac{{x + 2}}{2} = \frac{{y + 4}}{2} = \frac{{z + 1}}{1}\) và \((P):x + z + 24 = 0\);

b) \(d:\left\{ {\begin{array}{*{20}{l}}{x = 1 + t}\\{y =  - 1 + 2t}\\{z =  - 2 - t}\end{array}} \right.\) và \((P):2x + 4y - 2z + 23 = 0\).

Tính góc giữa đường thẳng \(d\) và mặt phẳng \((P)\) trong mỗi trường hợp sau:

a) \(d:\left\{ {\begin{array}{*{20}{l}}{x = 11 + 3t}\\{y =  - 11 + t}\\{z =  - 21 - 2t}\end{array}} \right.\) và \((P):6x + 2y - 4z + 7 = 0\);

b) \(d:\frac{{x - 3}}{2} = \frac{{y + 4}}{4} = \frac{{z - 5}}{2}\) và \((P):2x + 2y - 4z + 1 = 0\);

c) d: \(\frac{{x + 3}}{4} = \frac{{y + 5}}{4} = \frac{{z + 11}}{2}\) và \((P):2y - 4z + 7 = 0\).

Tính góc giữa hai mặt phẳng \((P)\) và \(\left( {{P^\prime }} \right)\) trong mỗi trường hợp sau:

a) \((P):x + y - 2z + 9 = 0\) và \(\left( {{P^\prime }} \right):3x - 5y + z + 2024 = 0\);

b) \((P):x + y + 24 = 0\) và \(\left( {{P^\prime }} \right):y + z + 24 = 0\);

c) \((P):2x + 4y - z + 23 = 0\) và \(\left( {{P^\prime }} \right):3x + 5y + 26z + 2025 = 0\).

Trong không gian Oxyz, cho hình chóp SABCD có đáy ABCD là hình chữ nhật và \(SA \bot (ABCD)\). Cho biết \(A(0;0;0),B(2;0;0),D(0;3;0),S(0;0;2)\).

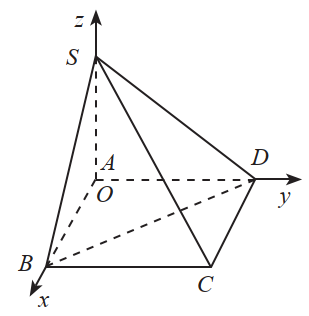
Tính góc giũa:

a) hai đường thằng SC và BD.

b) mặt phẳng (SBD) và mặt đáy;

c) đường thẳng SC và mặt phẳng \((SBD)\).

Tính góc giữa hai mặt phẳng \((P)\) và \(\left( {{P^\prime }} \right)\) trong mỗi trường hợp sau:

a) \((P):3x + 7y - z + 4 = 0\) và \(\left( {{P^\prime }} \right):x + y - 10z + 2025 = 0\);

b) \((P):x + y - 2z + 9 = 0\) và \(\left( {{P^\prime }} \right):3x - 5y + z + 2024 = 0\);

c) \((P):x + z + 3 = 0\) và \(\left( {{P^\prime }} \right):3y + 3z + 5 = 0\).

Trong không gian Oxyz, cho hình hộp chữ nhật \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Cho biết \(A(0;0;0)\), \(B(1;0;0),D(0;5;0),{A^\prime }(0;0;3)\). Tính góc giữa:

a) hai đường thẳng AC và \(B{A^\prime }\);

b) hai mă̆t phằng \(\left( {B{B^\prime }{D^\prime }D} \right)\) và \(\left( {A{A^\prime }{C^\prime }C} \right)\);

c) đường thẳng \(A{C^\prime }\) và mặt phẳng \(\left( {{A^\prime }BD} \right)\).

Tính góc giữa hai đường thẳng \(d:\frac{{x - 3}}{2} = \frac{{y + 5}}{4} = \frac{{z - 7}}{2}\) và \({d^\prime }:\frac{{x - 1}}{3} = \frac{{y + 7}}{3} = \frac{{z - 12}}{6}\).

Tính góc giữa đường thẳng \(d:\frac{{x + 2}}{2} = \frac{{y + 2}}{2} = \frac{{z - 1}}{1}\) và mặt phẳng \((P):3y - 3z + 1 = 0\).

Tính góc giữa hai mặt phẳng \((P):4y + 4z + 1 = 0\) và \(\left( {{P^\prime }} \right):7x + 7z + 2 = 0\).

Trong không gian Oxyz, cho hình lăng trụ đứng \(OBC.{O^\prime }{B^\prime }{C^\prime }\) có đáy là tam giác OBC vuông tại \(O\). Cho biết \(B(3;0;0),C(0;1;0),{O^\prime }(0;0;2)\). Tính góc giữa:

a) hai đường thẳng \(B{O^\prime }\) và \({B^\prime }C\);

b) hai mặt phẳng \(\left( {{O^\prime }BC} \right)\) và \((OBC)\);

c) đường thẳng \({B^\prime }C\) và mặt phẳng \(\left( {{O^\prime }BC} \right)\).

Trong không gian Oxyz, tính góc giữa hai đường thẳng: $\Delta :\left\{\begin{array}{l}x=1+t\\ y=-1+t\\ z=3\end{array}\text{ và }{\Delta }^{\text{'}}:\left\{\begin{array}{l}x=1+2s\\ y=-2+2s\\ z=4+s.\end{array}\right.\right.$

Ví dụ 6 Tính góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) biết:

${\Delta }_1:\left\{\begin{array}{l}x=1+t_1\\ y=2-\sqrt{3}{t}_1\\ z=3\end{array}\text{ và }{\Delta }_2:\left\{\begin{array}{l}x=4-\sqrt{3}{t}_2\\ y=5+t_2\\ z=6\end{array}\left(t_1,t_2\right.\right.\text{ là tham số). }\right.$

Cho hai đường thẳng \({\Delta _1}:\frac{{x - 1}}{3} = \frac{y}{2} = \frac{{z + 1}}{1},{\Delta _2}:\frac{x}{{ - 1}} = \frac{{y - 2}}{2} = \frac{{z - 3}}{{ - 1}}.\)

Chứng minh rằng \({\Delta _1} \bot {\Delta _2}\).

Cho đường thẳng \(\Delta :\frac{x}{2} = \frac{y}{{ - 1}} = \frac{z}{2}{\rm{. }}\)Tính côsin của góc giữa đường thẳng \(\Delta \) và các trục toạ độ.

Cho mặt phẳng \((P)\) có vectơ pháp tuyến \(\vec n = (1;2;2)\) và đường thẳng \(\Delta \) có vectơ chỉ phương \(\vec u = (2;2; - 1)\). Tính sin của góc giữa đường thẳng \(\Delta \) và mặt phẳng \((P)\). Góc giữa đường thẳng \(\Delta \) và mặt phẳng \((P)\) bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị)?a

Cho mặt phẳng \((P)\) có vectơ pháp tuyến \(\vec n = (A;B;C)\). Tính sin của góc giữa mặt phẳng \((P)\) và các trục toạ độ.

Tính góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):

a) \({\Delta _1}:\left\{ {\begin{array}{*{20}{l}}{x =  - 1 + {t_1}}\\{y = 4 + \sqrt 3 {t_1}}\\{z = 0}\end{array}} \right.\) và \({\Delta _2}:\left\{ {\begin{array}{*{20}{l}}{x =  - 1 + \sqrt 3 {t_2}}\\{y = 4 + {t_2}}\\{z = 5}\end{array}\quad \left( {{t_1},{t_2}} \right.} \right.\) là tham số);

b) \({\Delta _1}:\left\{ {\begin{array}{*{20}{l}}{x =  - 1 + 2t}\\{y = 3 + t}\\{z = 4 - t}\end{array}} \right.\) ( \(t\) là tham số) và \({\Delta _2}:\frac{{x + 1}}{3} = \frac{{y - 1}}{1} = \frac{{z - 4}}{{ - 2}}\);

c) \({\Delta _1}:\frac{{x + 3}}{1} = \frac{{y - 2}}{1} = \frac{{z - 1}}{{ - 1}}\) và \({\Delta _2}:\frac{{x + 2}}{{ - 1}} = \frac{{y - 2}}{3} = \frac{{z - 4}}{1}\).

Tính góc giữa đường thẳng \(\Delta \) và mặt phẳng \((P)\) dưới đây: \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = 1 + \sqrt 3 t}\\{y = 2}\\{z = 3 + t}\end{array}} \right.\) ( \(t\) là tham số) và \((P):\sqrt 3 x + z - 2 = 0\);

Tính góc giữa hai mặt phẳng \(\left( {{P_1}} \right):x + y + 2z - 1 = 0\) và \(\left( {{P_2}} \right):2x - y + z - 2 = 0\).

Trong không gian Oxyz, tính góc giữa đường thẳng \(d:\frac{x}{{ - 1}} = \frac{y}{2} = \frac{{z - 1}}{{ - 1}}\) và mặt phẳng \((\alpha ):x + y - 2z + 1 = 0\).

Trong không gian Oxyz, tính góc giữa hai mặt phẳng: \((\alpha ):2x + 2y - 4z + 1 = 0{\rm{ và }}(\beta ):x - z - 5 = 0.\)

Trong không gian vởi hệ tộ độ Oxyz, cho hình chóp S.ABCD có các đỉnh lần lượt là \(S\left( {0;0;\frac{{a\sqrt 3 }}{2}} \right),A\left( {\frac{a}{2};0;0} \right),B\left( { - \frac{a}{2};0;0} \right),C\left( { - \frac{a}{2};a;0} \right),D\left( {\frac{a}{2};a;0} \right)\) với \(a > 0(\) Hình 36).

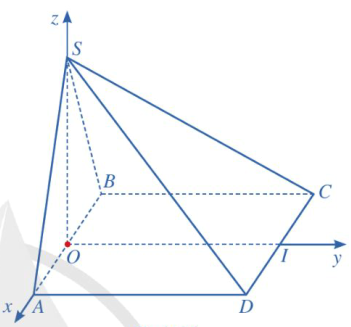
a) Xác định toạ độ của các vectơ \(\overrightarrow {SA} \), \(\overrightarrow {CD} \). Từ đó tính góc giữa hai đường thẳng SA và CD (làm tròn kết quả đến hàng đơn vị của độ).

b) Chỉ ra một vectơ pháp tuyến của mặt phẳng \((SAC)\). Từ đó tính góc giữa đường thẳng SD và mặt phẳng \((SAC)\) (làm tròn kết quả đến hàng đơn vị của độ).

Trong không gian với hệ tọa độ Oxyz, cho hình lăng trụ đứng \(OBC.{O^\prime }{B^\prime }{C^\prime }\) với \(O(0;0;0)\), \(B(2a;0;0),C(0;a;0),{O^\prime }(0;0;3a),a > 0\).

a) Xác định tọa độ của điểm \({B^\prime }\).

b) Viết phương trình mặt phẳng \(\left( {{O^\prime }BC} \right)\).

c) Tính sin của góc giữa đường thẳng \({B^\prime }C\) và mặt phẳng \(\left( {{O^\prime }BC} \right.\) ).

Trong không gian, cho hình lập phương \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }\).

a) Tính góc giữa hai mặt phẳng \((ABCD)\) và (CDA' \({B^\prime }\) ).

b) Tính góc giữa hai mặt phẳng \(\left( {BC{C^\prime }{B^\prime }} \right)\) và (CDA ' \(\left. {{B^\prime }} \right)\).

Cho hai mặt phẳng \(\left( {{P_1}} \right):\sqrt 3 x + z + 5 = 0\) và \(\left( {{P_2}} \right): - \sqrt 3 x + z - 7 = 0\).

Tính góc giữa hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\).

Cho mặt phẳng \((P)\) có vectơ pháp tuyến \(\vec n = (A;B;C).\) Tính côsin của góc giữa mặt phẳng \((P)\) và các mặt phẳng toạ độ.

Trong không gian Oxyz, tính góc giữa trục Oz và đường thẳng

\(\Delta :\frac{{x - 3}}{1} = \frac{{y + 1}}{2} = \frac{{z - 1}}{{ - 2}}.\)

Trong không gian Oxyz, tính góc tạo bởi trục Ox và mă̆t phẳng \((P):\sqrt 2 x - y + z + 2 = 0\).

Trong không gian Oxyz, tính góc giữa đường thẳng \(\Delta \) và mặt phẳng \((P)\), với:

\(\Delta :\frac{{x + 2}}{{ - 1}} = \frac{{y - 4}}{2} = \frac{{z + 1}}{1},(P):x - y + z - 1 = 0.\)

Trong không gian Oxyz, tính góc giữa hai mặt phẳng \((P):x + 2y + 2z - 1 = 0\) và (Q) : \(x + y - z + 1 = 0\).

Trong không gian Oxyz, tính góc giữa hai mặt phẳng \((P)\) : \(x - \sqrt 2 y + z - 2 = 0\) và \((Oxz):y = 0\).

Trong không gian Oxyz, cho \(A(0;0;4),B(0; - 3;0),C(0;3;0),D(3;0;0)\). Tính góc giữa hai mặt phẳng \((ABD)\) và \((ACD)\).

Trong không gian Oxyz, tính góc giữa hai đường thẳng:

\({\Delta _1}:\left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y = 1 - t}\\{z = 2 + 3t}\end{array}} \right.\) và \({\Delta _2}:\frac{{x - 2}}{{ - 1}} = \frac{{x + 1}}{1} = \frac{{z - 2}}{2}\).

Trong không gian Oxyz, tính góc giữa trục Oz và mặt phẳng \((P):x + 2y - z - 1 = 0\).

Tính góc giữa đường thẳng \(\Delta :\frac{{x + 1}}{{ - 1}} = \frac{{y - 3}}{2} = \frac{{z + 2}}{3}\) và mặt phẳng \((P):x + y + z + 3 = 0\).

Tính góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ nếu cần):

a) \({\Delta _1}:\left\{ {\begin{array}{*{20}{l}}{x = 3 + 2{t_1}}\\{y =  - 2 + {t_1}}\\{z = 0}\end{array}} \right.\) và \({\Delta _2}:\left\{ {\begin{array}{*{20}{l}}{x = 7 + {t_2}}\\{y =  - 3 - {t_2}}\\{z = 2{t_2}}\end{array}\left( {{t_1},{t_2}} \right.} \right.\) là tham số);

b) \({\Delta _1}:\left\{ {\begin{array}{*{20}{l}}{x = 3 + t}\\{y = 5 - 2t}\\{z = 7 - 2t}\end{array}} \right.\) ( là tham số) và \({\Delta _2}:\frac{{x + 4}}{2} = \frac{{y + 6}}{2} = \frac{{z - 10}}{{ - 1}}\);

c) \({\Delta _1}:\frac{{x + 1}}{{ - 1}} = \frac{{y + 4}}{2} = \frac{{z - 5}}{{ - 3}}\) và \({\Delta _2}:\frac{x}{2} = \frac{{y - 3}}{{ - 1}} = \frac{{z + 2}}{{ - 1}}\).

Tính góc giữa đường thẳng \(\Delta \) và mặt phẳng \((P)\) trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):

a) \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = 18 - \sqrt 3 t}\\{y = 11}\\{z = 5 + t}\end{array}\quad } \right.\) ( \(t\) là tham số) và \((P):x - \sqrt 3 y - z - 3 = 0\);

b) \(\Delta :\frac{{x - 8}}{2} = \frac{{y - 7}}{{ - 3}} = \frac{{z - 6}}{3}\) và \((P):3x - 4y + 5z - 6 = 0\).

Tính góc giữa mặt phẳng \((P):x - y = 0\) và mặt phẳng \((Oyz)\).

Cho hai đường thẳng \({\Delta _1}:\left\{ {\begin{array}{*{20}{l}}{x = 11 - 3{t_1}}\\{y =  - 5 + 4{t_1}}\\{z = m{t_1}}\end{array}} \right.\) và \({\Delta _2}:\left\{ {\begin{array}{*{20}{l}}{x =  - 4 + 5{t_2}}\\{y = 2 + 3{t_2}}\\{z = 2{t_2}}\end{array}} \right.\) :với \(m\) là tham số thực; \({t_1},{t_2}\) là tham số của phương trình đường thẳng. Tìm \(m\) để hai đường thẳng đó vuông góc với nhau.