24 câu trắc nghiệm Toán 12 Chân trời sáng tạo Bài 2. Phương trình đường thẳng trong không gian (Đúng sai - Trả lời ngắn) có đáp án
24 câu hỏi
Cho đường thẳng 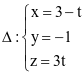 . Vectơ nào sau đây là vectơ chỉ phương của △?
. Vectơ nào sau đây là vectơ chỉ phương của △?
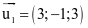 .
.
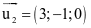 .
.
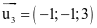 .
.
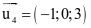 .
.
Trong không gian Oxyz, cho đường thẳng 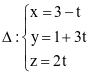 , điểm nào dưới đây thuộc đường thẳng △?
, điểm nào dưới đây thuộc đường thẳng △?
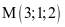 .
.
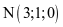 .
.
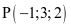 .
.
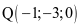 .
.
Trong không gian tọa độ Oxyz, cho đường thẳng 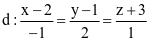 . Vectơ nào dưới đây là một vectơ chỉ phương của d?
. Vectơ nào dưới đây là một vectơ chỉ phương của d?
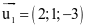 .
.
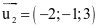 .
.
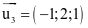 .
.
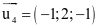 .
.
Trong không gian với hệ tọa độ Oxyz, phương trình tham số của đường thẳng đi qua điểm M(3; −1; 2) và có vectơ chỉ phương 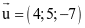 là
là
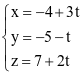 .
.
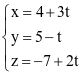 .
.
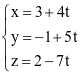 .
.
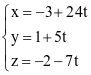 .
.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(1; −2; 1), N(0; 1; 3). Phương trình đường thẳng qua hai điểm M, N là
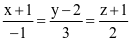 .
.
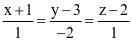 .
.
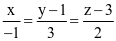 .
.
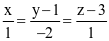 .
.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 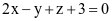 và điểm A(1; −2; 1). Phương trình đường thẳng đi qua A và vuông góc với (P) là
và điểm A(1; −2; 1). Phương trình đường thẳng đi qua A và vuông góc với (P) là
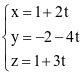 .
.
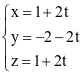 .
.
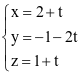 .
.
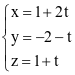 .
.
Trong không gian Oxyz, cho điểm A(1; 2; 3) và đường thẳng 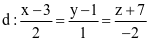 . Đường thẳng đi qua A và song song với d có phương trình là
. Đường thẳng đi qua A và song song với d có phương trình là
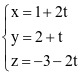 .
.
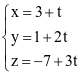 .
.
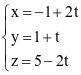 .
.
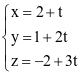 .
.
Trong không gian Oxyz, vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm M(2; 3; −1) và N(4; 5; 3)?
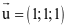 .
.
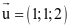 .
.
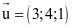 .
.
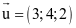 .
.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng 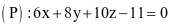 và đường thẳng
và đường thẳng 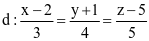 . Khi đó côsin của góc tạo bởi đường thẳng d và mặt phẳng (P) bằng
. Khi đó côsin của góc tạo bởi đường thẳng d và mặt phẳng (P) bằng
0.
1.
−1.
0,5.
Trong không gian Oxyz, gọi α là góc giữa hai mặt phẳng (P): 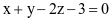 và
và 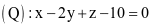 . Khi đó
. Khi đó 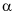 bằng
bằng
30°.
45°.
60°.
90°.
Trong không gian với hệ tọa độ Oxyz, gọi α là góc giữa hai đường thẳng 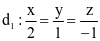 và
và 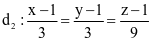 . Khi đó cosα bằng
. Khi đó cosα bằng
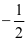 .
.
0.
1.
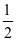 .
.
Trong không gian Oxyz, tính góc tạo bởi trục Ox và mặt phẳng 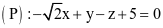 .
.
30°.
45°.
60°.
90°.
Trong không gian Oxyz, cho hai đường thẳng 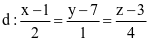 và
và 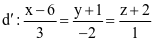 .
.
Trong các mệnh đề sau, mệnh đề nào đúng?
song song.
trùng nhau.
cắt nhau.
chéo nhau.
Trong không gian Oxyz, cho hai đường thẳng 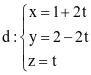 và
và 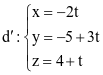 . Trong các mệnh đề sau, mệnh đề nào đúng?
. Trong các mệnh đề sau, mệnh đề nào đúng?
song song.
trùng nhau.
cắt nhau.
chéo nhau.
Trong không gian Oxyz, cho đường thẳng 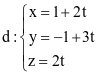 .
.
(a) Đường thẳng đi qua điểm A(1; −1; 0).
(b) Một vectơ chỉ phương của đường thẳng d là 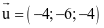 .
.
(c) Đường thẳng d song song với đường thẳng 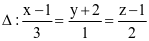 .
.
(d) Đường thẳng d và 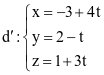 chéo nhau.
chéo nhau.
Trong không gian với hệ tọa độ Oxyz cho điểm A(1; 1; 2) và đường thẳng 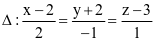 .
.
(a) Điểm A không thuộc đường thẳng △.
(b) Một vectơ chỉ phương của △ là 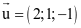 .
.
(c) Hình chiếu của A lên đường thẳng △ là H(0; −1; 2).
(d) Phương trình mặt phẳng đi qua A và vuông góc với đường thẳng △ là 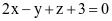 .
.
Trong không gian Oxyz, cho đường thẳng 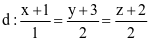 và điểm A(3; 2; 0).
và điểm A(3; 2; 0).
(a) Đường thẳng d đi qua điểm A(3; 2; 0).
(b) Đường thẳng d có một vectơ chỉ phương là 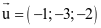 .
.
(c) H(1; 1; 2) là hình chiếu của A lên đường thẳng d.
(d) A'(−1; 0; 4) là điểm đối xứng với A qua đường thẳng d.
Trong không gian Oxyz, cho đường thẳng 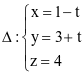 và mặt phẳng
và mặt phẳng 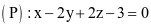 .
.
(a) 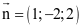 là một vectơ pháp tuyến của (P).
là một vectơ pháp tuyến của (P).
(b) Điểm M(0; 4; 4) thuộc △.
(c) Góc giữa và (P) bằng 60°.
(d) Đường thẳng d đi qua điểm M(0; 4; 4), song song với (P) và tạo với △ một góc 45° có phương trình là 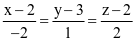 .
.
Trong không gian Oxyz, cho hai đường thẳng 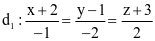 ;
; 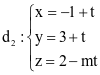 .
.
(a) Khi m = 0, số đo góc giữa hai đường thẳng d1 và d2 bằng 135°.
(b) 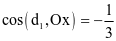 .
.
(c) Đường thẳng △ đi qua gốc tọa độ O và vuông góc với (P): 2x + 2y + z – 4 = 0 tạo với đường thẳng d1 một góc α có 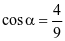 .
.
(d) Khi 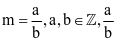 là phân số tối giản, số đo góc giữa hai đường thẳng d1 và d2 bằng 90°. Giá trị biểu thức
là phân số tối giản, số đo góc giữa hai đường thẳng d1 và d2 bằng 90°. Giá trị biểu thức 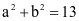 .
.
Một robot di chuyển theo đường thẳng d có phương trình 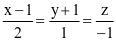 . Mặt tường của nhà kho có phương trình
. Mặt tường của nhà kho có phương trình 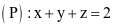 . Tọa độ điểm mà robot sẽ chạm vào tường có dạng (a; b; c). Tính a + b + c.
. Tọa độ điểm mà robot sẽ chạm vào tường có dạng (a; b; c). Tính a + b + c.
Để làm thí nghiệm về chuyển động trong mặt phẳng nghiêng, người làm thí nghiệm đã thiết lập sẵn một hệ tọa độ Oxyz. Góc giữa mặt phẳng nghiêng (P): 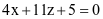 và mặt sàn (Q): z – 1 = 0 là bao nhiêu độ (làm tròn kết quả đến hàng đơn vị của độ)?
và mặt sàn (Q): z – 1 = 0 là bao nhiêu độ (làm tròn kết quả đến hàng đơn vị của độ)?
Một phần mềm mô phỏng vận động viên đang tập bắn súng trong không gian Oxyz. Cho biết trục d của nòng súng có phương trình 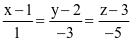 và hồng tâm A(8; −19; 6m + 4). Hỏi m bằng bao nhiêu vận động viên đó bắn trúng hồng tâm?
và hồng tâm A(8; −19; 6m + 4). Hỏi m bằng bao nhiêu vận động viên đó bắn trúng hồng tâm?
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng 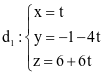 và
và 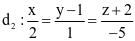 . Phương trình chính tắc của đường thẳng d3 đi qua M(1; −1; 2) và vuông góc với cả d1; d2 có dạng
. Phương trình chính tắc của đường thẳng d3 đi qua M(1; −1; 2) và vuông góc với cả d1; d2 có dạng 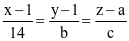 . Tính a + b + c.
. Tính a + b + c.
Trong không gian Oxyz cho hai đường thẳng 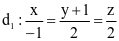 và
và 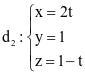 . Gọi
. Gọi 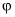 là góc giữa hai đường thẳng d1, d2. Giá trị
là góc giữa hai đường thẳng d1, d2. Giá trị 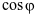 có dạng
có dạng 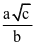 . Tính giá trị biểu thức
. Tính giá trị biểu thức 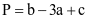 .
.








