(Trả lời ngắn) 23 bài tập Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn (có lời giải)

Trong 5 giây đầu tiên, một chất điểm chuyển động theo phương trình \(s\left( t \right) =  - {t^3} + 6{t^2} + t + 5\)trong đó \(t\) tính bằng giây và \(s\) tính bằng mét. Chất điểm có vận tốc tức thời lớn nhất bằng bao nhiêu trong 5 giây đầu tiên đó?

Một tên lửa bay vào không trung với quãng đường đi được là \(s\left( t \right)\) (km) là hàm phụ thuộc theo biến \(t\) (giây) tuân theo biểu thức sau: \(s\left( t \right) = {e^{{t^2} + 3}} + 2t{e^{3t + 1}}\) (km). Vận tốc của tên lửa sau 1 giây là \(m.{e^n}\) (km/s). Tính \(T = m + n\)  (Biết hàm biểu thị vận tốc là đạo hàm cấp một của hàm biểu thị quãng đường theo thời gian)?

Một vật được phóng thẳng đứng lên trên từ độ cao \(2\;\)m với vận tốc ban đầu là \(24,5\;\)(m/s). Trong Vật lý, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao \(h\) (mét) của vật sau \(t\) (giây) được cho bởi công thức \(h\left( t \right) = 2 + 24,5t - 4,9{t^2}.\) Hỏi sau bao nhiêu giây thì vật đạt độ cao lớn nhất?

Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật Logistic được mô hình hoá bằng hàm số \(f\left( t \right) = \frac{{5000}}{{1 + 5{e^{ - t}}}},t \ge 0,\)trong đó thời gian \(t\) được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm \(f'\left( t \right)\) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?

Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức: \[N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}}({\rm{con}}),\]trong đó \(t\) là thời gian tính bằng giây. Tính số lượng vi khuẩn lớn nhất kể từ khi thực hiện cấy vi khuẩn vào môi trường dinh dưỡng.

Ho ép khí quản co lại, ảnh hưởng đến tốc độ của không khí đi vào khí quản. Tốc độ của không khí đi vào khí quản khi ho được cho bởi công thức \(V = k\left( {R - r} \right){r^2}{\rm{; }}0 \le r < R,\)trong đó \(k\) là hằng số, \(R\) là bán kính bình thường của khí quản, \(r\) là bán kính khí quản khi ho. Hỏi bán kính của khí quản khi ho bằng bao nhiêu so với bán kính khí quản lúc bình thường thì tốc độ của không khí đi vào khí quản là lớn nhất?

Người quản lí của một khu chung cư có 100 căn hộ cho thuê nhận thấy rằng tất cả các căn hộ sẽ có người thuê nếu giá thuê một căn hộ là 8 triệu đồng một tháng. Một cuộc khảo sát thị trường cho thấy rằng, trung bình cứ mỗi lần tăng giá thuê căn hộ thêm 100 nghìn đồng thì sẽ có thêm một căn hộ bị bỏ trống. Người quản lí nên đặt giá thuê mỗi căn hộ là bao nhiêu để doanh thu là lớn nhất?

Giả sử chi phí tiền xăng \(C\) (đồng) phụ thuộc tốc độ trung bình \(v\)(km/h) theo công thức:

\(C\left( v \right) = \frac{{16000}}{v} + \frac{5}{2}v\,\,\,\left( {0 < v \le 120} \right)\)

Để biểu diễn trực quan sự thay đổi của \(C\left( v \right)\) theo \(v\), người ta đã vẽ đồ thị hàm số \(C\left( v \right)\) như hình bên.

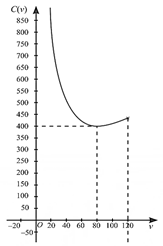
Tài xế xe tải lái xe với tốc độ trung bình là bao nhiêu để tiết kiệm tiền xăng nhất?

Một công ty kinh doanh bất động sản có 20 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2 triệu đồng/1 tháng thì tất cả các căn hộ đều có người thuê. Nhưng cứ mỗi lần tăng giá cho thuê mỗi căn hộ thêm 200 nghìn đồng/1 tháng thì có thêm một căn hộ bị bỏ trống. Hỏi công ty nên cho thuê mỗi căn hộ bao nhiêu tiền một tháng để tổng số tiền thu được là lớn nhất?

Một con cá hồi bơi ngược dòng nước để vượt một khoảng cách là \(300\;\)km. Vận tốc dòng nước là \(6\)(km/h). Nếu vận tốc bơi của cá khi nước đứng yên là \(v\)(km/h) thì năng lượng tiêu hao của cá trong \(t\) giờ được cho bởi công thức \(E\left( v \right) = c{v^3}t\) (trong đó \(c\) là hằng số dương, \(E\) được tính bằng đơn vị Jun). Cá bơ ngược dòng quãng đường \(300\;\)km trên trong khoảng thời gian \[t\] với vận tốc bằng bao nhiêu để năng lượng tiêu hao là thấp nhất?

Thể tích \(V\) của \(1\;\)(kg) nước ở nhiệt độ \(t\) (\(t\) nằm giữa $0^{°}C$ đến ${30}^{°}C$ được cho bởi công thức

\(V = 999,87 - 0,06426t + 0,0085043{t^2} - 0,0000679{t^3}\left( {{m^3}} \right).\)

Ở nhiệt độ bao nhiêu độ C thì nước có khối lượng riêng lớn nhất?

Một công ty đánh giá rằng sẽ bán được \(N\) lô hàng nếu chi hết số tiền là \(x\) (triệu đồng) vào việc quảng cáo. Biết rằng \(N\) và \(x\) liên hệ với nhau bằng biểu thức \(N\left( x \right) =  - {x^2} + 30x + 6,0 \le x \le 30\). Hãy tìm số lô hàng lớn nhất mà công ti có thể bán sau đợt quảng cáo?

Công ti truyền hình cáp Vista hiện có 100000 thuê bao. Mỗi thuê bao đang trả cước thuê bao 40$/ tháng. Một cuộc khảo sát cho thấy cứ mỗi lần giảm $\mathrm{0,25}\$$ cước thuê bao, công ti có thể có thêm 1000 thuê bao. Để doanh thu thu được là tối đa, công ti cần xác định mức cước thuê bao mỗi tháng là bao nhiêu?

Một bài báo trong tạp chí xã hội học phát biểu rằng nếu một chương trình chăm sóc sức khỏe đặc biệt cho người già được khởi xướng, thì \(t\) năm sau khi nó được khởi động, \[n\] ngàn người già có thể trực tiếp nhận được các phúc lợi, trong đó \(n = \frac{{{t^3}}}{3} - 6{t^2} + 32t\,\,\,\left( {0 \le t \le 12} \right)\). Với giá trị nào của \[t\] thì số người nhận phúc lợi tối đa là bao nhiêu?

Một chất điểm chuyển động có phương trình chuyển động là \[s =  - {t^3} + 6{t^2} + 17t\], với \[t\left( s \right)\] là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và \[s\left( m \right)\] là quãng đường vật đi được trong khoảng thời gian đó. Trong khoảng thời gian 8 giây đầu tiên, vận tốc \[v\left( {m/s} \right)\]của chất điểm đạt giá trị lớn nhất bằng?

Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất \(8000\) quả bóng tennis. Công ty này sở hữu một số máy móc, mỗi máy có thể sản xuất \(30\) quả bóng trong một giờ. Chi phí thiết lập các máy này là \(200\) nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giám sát. Số tiền phải trả cho người giám sát là \(192\) nghìn đồng một giờ. Số máy móc công ty nên sử dụng là bao nhiêu để chi phí hoạt động là thấp nhất?

Cắt một đoạn dây dài \(60{\rm{m}}\)thành hai đoạn dây, đoạn dây thứ nhất gấp thành một tam giác đều có diện tích \({S_1}\), đoạn dây thứ hai gấp thành một hình vuông có diện tích \({S_2}\) (như hình vẽ dưới)

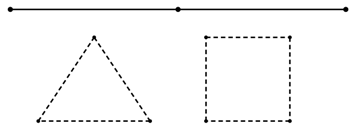
Khi đó giá trị nhỏ nhất của tổng \(T = {S_1} + {S_2}\) là bao nhiêu?

Cắt một đoạn dây dài \(30{\rm{m}}\)thành hai đoạn dây, đoạn dây thứ nhất gấp thành một đường tròn có diện tích \({S_1}\), đoạn dây thứ hai gấp thành một hình vuông có diện tích \({S_2}\) (như hình vẽ dưới)

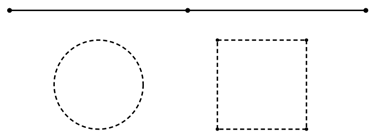
Khi đó giá trị nhỏ nhất của tổng \(T = {S_1} + {S_2}\) là bao nhiêu?

Một cái hộp có dạng hình hộp chữ nhật có thể tích bằng \[48\] và chiều dài gấp đôi chiều rộng. Chất liệu làm đáy và \[4\] mặt bên của hộp có giá thành gấp ba lần giá thành của chất liệu làm nắp hộp. Gọi \[h\] là chiều cao của hộp để giá thành của hộp là thấp nhất. Biết \[h = \frac{m}{n}\] với \[m\], \[n\] là các số nguyên dương nguyên tố cùng nhau. Tổng \[m + n\] bằng bao nhiêu?

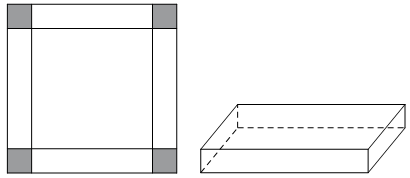
Một tấm bìa hình vuông có diện tích \(900\,{\rm{c}}{{\rm{m}}^2}\). Người ta cắt ở bốn góc của tấm bìa đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng \(x\) cm rồi gập tấm bìa lại như hình vẽ bên để được một cái hộp không nắp có dạng hình hộp chữ nhật. Tìm thể tích lớn nhất mà hình hộp chữ nhật có thể thu được?

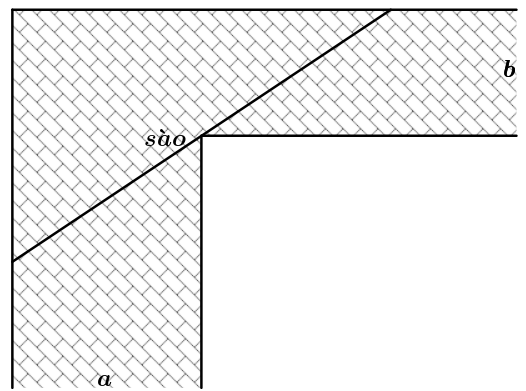
Một người nông dân có \(15\,\,000\,\,000\)đồng để làm một hàng rào hình chữ \(E\) dọc theo một con sông bao quanh hai khu đất trồng rau có dạng hai hình chữ nhật bằng nhau (hình vẽ dưới). Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là \(60\,\,000\) đồng/mét, còn đối vối ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là \(50\,\,000\) đồng/mét, mặt giáp với bờ sông không phải rào. Tìm diện tích lớn nhất của hai khu đất thu được sau khi làm hàng rào.

Để chặn đường hành lang hình chữ L, người ta dùng một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ). Biết \[a = 24\] và \[b = 3\]. Hỏi cái sào thỏa mãn điều kiện trên có chiều dài tối thiểu là bao nhiêu?