(Trả lời ngắn) 17 bài tập Phương trình mặt cầu (có lời giải)

Trong không gian với hệ trục tọa độ \[Oxyz\], tìm tất cả các giá trị của \[m\] để phương trình \[{x^2} + {y^2} + {z^2} - 2\left( {m + 2} \right)x + 4my + 19m - 6 = 0\] là phương trình mặt cầu.

Trong không gian với hệ tọa độ \(Oxyz\), cho \(A\left( { - 1;0;0} \right)\), \(B\left( {0;0;2} \right)\), \(C\left( {0; - 3;0} \right)\). Tính bán kính mặt cầu ngoại tiếp tứ diện \(OABC\).

Trong không gian \(Oxyz\), gọi \(I\left( {a;\,b;\,c} \right)\) là tâm mặt cầu đi qua điểm \(A\left( {1;\, - 1;\,4} \right)\) và tiếp xúc với tất cả các mặt phẳng tọa độ. Tính \(P = a - b + c\).

Trong không gian \(Oxyz\), tìm giá trị dương của \(m\) sao cho mặt phẳng \(\left( {Oxy} \right)\) tiếp xúc với mặt cầu \({\left( {x - 3} \right)^2} + {y^2} + {\left( {z - 2} \right)^2} = {m^2} + 1\).

Trong không gian với hệ trục tọa độ \[Oxyz\], cho ba điểm \[A\left( {1;2; - 4} \right)\], \[B\left( {1; - 3;1} \right)\], \[C\left( {2;2;3} \right)\]. Tính đường kính của mặt cầu \[\left( S \right)\] đi qua ba điểm trên và có tâm nằm trên mặt phẳng \[\left( {Oxy} \right)\].

Trong không gian \(Oxyz\), gọi \(\left( S \right)\) là mặt cầu đi qua điểm \(D\left( {0\,;\,1\,;\,2} \right)\) và tiếp xúc với các trục \(Ox\), \(Oy\), \(Oz\) tại các điểm \[A\left( {a\,;\,0\,;\,0} \right)\], \[B\left( {0\,;\,b\,;\,0} \right)\], \(C\left( {0\,;\,0\,;\,c} \right)\) trong đó \[a,{\rm{ }}b,{\rm{ }}c \in \mathbb{R}\backslash \left\{ {0\,;\,1} \right\}\]. Tính bán kính của \(\left( S \right)\).

Trong không gian với hệ trục tọa độ \(Oxyz\), cho ba điểm \(A\left( {1;0;0} \right)\), \(C\left( {0;0;3} \right)\), \(B\left( {0;2;0} \right)\). Tập hợp các điểm \(M\) thỏa mãn \(M{A^2} = M{B^2} + M{C^2}\) là mặt cầu có bán kính là bao nhiêu?

Trong không gian \(Oxyz\), xét mặt cầu \(\left( S \right)\) có phương trình dạng \({x^2} + {y^2} + {z^2} - 4x + 2y - 2az + 10a = 0\). Tập hợp các giá trị thực của \(a\) để \(\left( S \right)\)có chu vi đường tròn lớn bằng \(8\pi \).

Trong không gian với hệ trục tọa độ \[Oxyz\], cho mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\) và hình nón \(\left( H \right)\) có đỉnh \(A\left( {3;2; - 2} \right)\) và nhận \(AI\) làm trục đối xứng với \(I\) là tâm mặt cầu. Một đường sinh của hình nón \(\left( H \right)\) cắt mặt cầu tại \(M,{\rm{ }}N\) sao cho \(AM = 3AN\). Viết phương trình mặt cầu đồng tâm với mặt cầu \(\left( S \right)\) và tiếp xúc với các đường sinh của hình nón \(\left( H \right)\).

Trong mặt phẳng tọa độ \(Oxyz\), cho bốn điểm \(A\left( {0; - 1;2} \right)\), \(B\left( {2; - 3;0} \right)\), \(C\left( { - 2;1;1} \right)\), \(D\left( {0; - 1;3} \right)\). Gọi \(\left( L \right)\) là tập hợp tất cả các điểm \(M\) trong không gian thỏa mãn đẳng thức \(\overrightarrow {MA} .\overrightarrow {MB}  = \overrightarrow {MC} .\overrightarrow {MD}  = 1\). Biết rằng \(\left( L \right)\) là một đường tròn, đường tròn đó có bán kính \(r\) bằng bao nhiêu?

Từ mặt nước trong một bể nước, tại ba vị tri đôi một cách nhau 2 m , người ta lần lượt thả dầy dọi để quả dọi chạm đáy bể. Phần dây dọi (thẳng) nằm trong nước tại ba vị tri đó lần lượt có độ dài \(4\;{\rm{m}};4,4\;{\rm{m}};4,8\;{\rm{m}}\). Biết đáy bể là phẳng. Hỏi đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ?

Bản vẽ thiết kế của một công trình được vẽ trong một hệ trục toạ độ Oxyz. Sàn nhà của công trình thuộc mặt phẳng Oxy , đường ống thoát nước thẳng và đi qua hai điểm \(A(1;2; - 1)\) và \(B(5;6; - 2)\). Tính góc tạo bởi đường ống thoát nước và mặt sàn.

Né́u đứng trước biển và nhìn ra xa, người ta sẽ thấy một đường giao giữa mặt biển và bầu trời, đó là đường chân trời đối với người quan sát (H.5.45a). Về mặt Vật lí, đường chân trời là đường giới hạn phần Trái Đất mà người quan sát có thể nhìn thấy được (phần còn lại bị chính Trái Đất che khuất). Ta có thể hình dung rằng, nếu người quan sát ở tại đỉnh của một chiếc nón và Trái Đát được "thả" vào trong chiếc nón đó, thì đường chân trời trong trường hợp này là đường chạm giữa Trái Đất và chiếc nón (H.5.45b). Trong mô hình toán học, đường chân trời đối với người quan sát tại vị trí \(B\) là tập hợp những điểm \(A\) nằm trên bề mặt Trái Đất sao cho $\widehat{\text{BAO}}={90}^{°}$, với O là tâm Trái Đất (H.5.45c). Trong không gian Oxyz, giả sử bề mặt Trái Đất \((S)\) có phương trình \({x^2} + {y^2} + {z^2} = 1\) và người quan sát ở vị trí \(B(1,1; - 1)\).

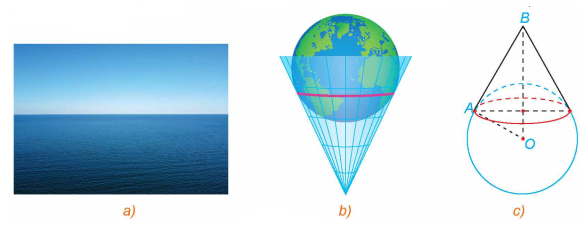
Gọi \(A\) là một vị trí bất kì trên đường chân trời đối với người quan sát ở vị trí \(B\). Tính khoảng cách AB.

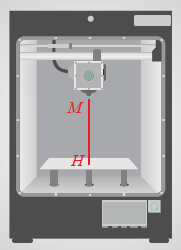
Phần mềm điều khiền máy in 3 D cho biết đầu in phun của máy đang đặt tại điểm \(M(3;4;24)\) (đơn vị: cm ). Tính khoàng cách từ đầu in đến khay đặt vật in có phương trình \(z - 4 = 0\).

Trong không gian hệ trục tọa độ \(Oxyz\) (đơn vị trên mỗi trục là kilômét) một trạm phát sóng điện thoại của nhà mạng Vinaphone được đặt ở vị trí \(I\left( {1; - 2; - 3} \right)\) và được thiết kế bán kính phủ sóng là \(5000m\).

a) Sử dụng phương trình mặt cầu để mô tả ranh giới bên ngoài vùng phủ sóng trong không gian.

b) Nhà bạn Minh Hiền và bạn Trúc Linh có vị trí tọa độ lần lượt là \(M\left( {1;2;0} \right)\) và \(N\left( { - 3;1;0} \right)\). Hỏi Minh Hiền và Trúc Linh dùng điện thoại tại nhà thì có thể sử dụng dịch vụ của trạm này không?

Trong không gian hệ trục tọa độ \(Oxyz\) (đơn vị trên mỗi trục là kilômét) một trạm phát sóng rađa của Nga được đặt trên bán đảo Crimea ở vị trí \(I\left( { - 2;1; - 1} \right)\) và được thiết kế phát hiện máy bay của địch ở khoảng cách tối đa \(500km\).

a) Sử dụng phương trình mặt cầu để mô tả ranh giới bên ngoài vùng phát sóng của rađa trong không gian.

b) Hai chiếc máy bay do thám của Mỹ và Anh đang bay ở vị trí có tọa độ lần lượt là \(M\left( { - 200;100; - 250} \right)\) và \(N\left( {350; - 100;300} \right)\). Hỏi rađa của Nga có thể phát hiện ra hai chiếc máy bay do thám của Mỹ và Anh không?