23 bài tập Một số dạng toán thực tế liên quan đến Phương trình mặt cầu (có lời giải)

Công nghệ hỗ trợ trọng tài VAR (Video Assistant Referee) thiết lập một hệ tọa độ Oxyz để theo dõi vị trí của quả bóng \(M\). Cho biết \(M\) đang nằm trên mặt sân có phương trình \(z = 0\), đồng thời thuộc mặt cầu \((S):{(x - 32)^2} + {(y - 50)^2} + {(z - 10)^2} = 109\) (đơn vị độ dài tính theo mét).

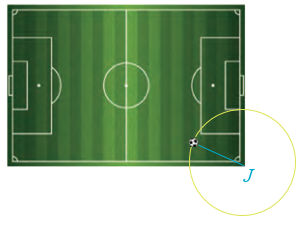
a) Tìm toạ độ tâm \(I\) và bán kính \(R\) của mặt cầu \((S)\).

b) Tìm toạ độ hình chiếu vuông góc \(J\) của tâm \(I\) trên mặt sân.

c) Tính khoảng cách từ vị trí \(M\) của quả bóng đến điểm \(J\).

Trong không gian Oxyz (đơn vị của các trục toạ độ là kilômét), một trạm thu phát sóng điện thoại di động có đầu thu phát được đặt tại điềm \(I( - 6; - 1;4)\).

a) Cho biết bán kính phủ sóng của trạm là 2 km . Viết phương trình mặt cầu \((S)\) biểu diễn ranh giới của vùng phủ sóng.

b) Một người sử dụng điện thoại tại điểm \(M( - 5; - 2;5)\). Hãy cho biết điểm \(M\) nằm trong hay nằm ngoài mặt cầu \((S)\) và người đó có thể sử dụng được dịch vụ của trạm nói trên hay không.

c) Câu hỏi tương tự đối với người sử dụng điện thoại ở điểm \(N( - 1;0;1)\).

Bề mặt của một bóng thám không dạng hình cầu có phương trình:

\({x^2} + {y^2} + {z^2} - 200x - 600y - 4000z + 4099900 = 0.{\rm{ }}\)

Tìm toạ độ tâm và bán kính mặt cầu.

Đầu in phun của một máy in 3D đang in bề mặt của một mặt cầu có phương trình:

\({x^2} + {y^2} + {z^2} + \frac{1}{8}x - \frac{1}{8}y - z + \frac{1}{{16}} = 0.\)

Tính khoảng cách từ đầu in phun đến tâm mặt cầu.

Phần mềm mô phỏng thiết bị thám hiểm đại dương có dạng hình cầu trong không gian Oxyz. Cho biết toạ độ tâm mặt cầu là \(I(360;200;400)\) và bán kính \(r = 2\;{\rm{m}}\). Viết phương trình mặt cầu.

Trong không gian Oxyz, một thiết bị phát sóng đặt tại vị trí \(A(2;0;0)\). Vùng phủ sóng của thiết bị có bán kinh bằng 1 . Hỏi vị trí \(M(2;1;1)\) có thuộc vưng phư sóng của thiết bị nói trên hay không?

Biết rằng nếu vị trí M có vĩ độ và kinh độ tương ứng là ${\alpha }^{°}N,{\beta }^{°}E(0<\alpha <90, 0<\beta <90)$ thì có toạ độ $M\left(\cos {\alpha }^{°}\cos {\beta }^{°};\cos {\alpha }^{°}\sin {\beta }^{°};\sin {\alpha }^{°}\right)$. Tính khoảng cách trên mặt đất từ vị trí  đến vị trí $Q:{80}^{°}\text{N}{\mathrm{,70}}^{°}\text{E}$.

Tính khoảng cách trên mặt đất từ vị trí A là giao giữa kinh tuyến gốc với xích đạo đến vị trí $B:{45}^{°}\text{N}{\mathrm{,30}}^{°}\text{E}$.

Từ mặt nước trong một bể nước, tại ba vị tri đôi một cách nhau 2 m , người ta lần lượt thả dầy dọi để quả dọi chạm đáy bể. Phần dây dọi (thẳng) nằm trong nước tại ba vị tri đó lần lượt có độ dài \(4\;{\rm{m}};4,4\;{\rm{m}};4,8\;{\rm{m}}\). Biết đáy bể là phẳng. Hỏi đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ?

Bản vẽ thiết kế của một công trình được vẽ trong một hệ trục toạ độ Oxyz. Sàn nhà của công trình thuộc mặt phẳng Oxy , đường ống thoát nước thẳng và đi qua hai điểm \(A(1;2; - 1)\) và \(B(5;6; - 2)\). Tính góc tạo bởi đường ống thoát nước và mặt sàn.

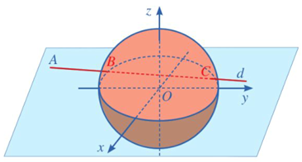
Né́u đứng trước biển và nhìn ra xa, người ta sẽ thấy một đường giao giữa mặt biển và bầu trời, đó là đường chân trời đối với người quan sát (H.5.45a). Về mặt Vật lí, đường chân trời là đường giới hạn phần Trái Đất mà người quan sát có thể nhìn thấy được (phần còn lại bị chính Trái Đất che khuất). Ta có thể hình dung rằng, nếu người quan sát ở tại đỉnh của một chiếc nón và Trái Đát được "thả" vào trong chiếc nón đó, thì đường chân trời trong trường hợp này là đường chạm giữa Trái Đất và chiếc nón (H.5.45b). Trong mô hình toán học, đường chân trời đối với người quan sát tại vị trí \(B\) là tập hợp những điểm \(A\) nằm trên bề mặt Trái Đất sao cho $\widehat{\text{BAO}}={90}^{°}$, với O là tâm Trái Đất (H.5.45c). Trong không gian Oxyz, giả sử bề mặt Trái Đất \((S)\) có phương trình \({x^2} + {y^2} + {z^2} = 1\) và người quan sát ở vị trí \(B(1,1; - 1)\).

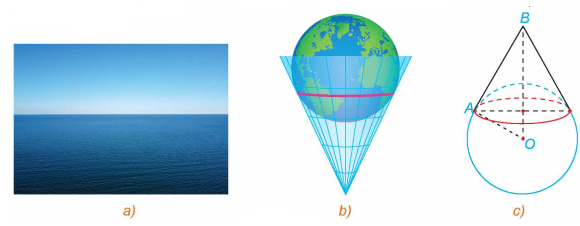
Gọi \(A\) là một vị trí bất kì trên đường chân trời đối với người quan sát ở vị trí \(B\). Tính khoảng cách AB.

Người ta muốn thiết kế một bồn chứa khí hoá lòng hình cầu bằng phần mềm 3D . Cho biết phương trình bề mặt của bồn chứa là \((S)\) : \({(x - 6)^2} + {(y - 6)^2} + {(z - 6)^2} = 25\). Phương trình mặt phẳng chứa nắp là \((P):z = 10\).

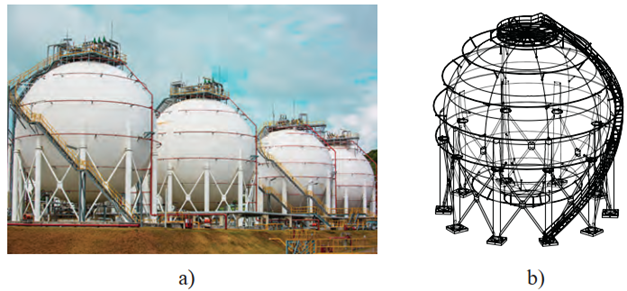
a) Tìm tâm và bán kính của bồn chứa.

b) Tính khoảng cách từ tâm bồn chứa đến mặt phẳng chứa nắp.

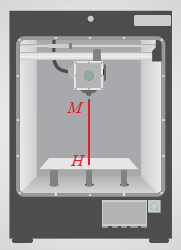
Phần mềm điều khiền máy in 3 D cho biết đầu in phun của máy đang đặt tại điểm \(M(3;4;24)\) (đơn vị: cm ). Tính khoàng cách từ đầu in đến khay đặt vật in có phương trình \(z - 4 = 0\).

Phần mềm của máy tiện kĩ thuật số CNC (Computer Numerical Control) đang biểu diễn một chi tiết máy như Hình vẽ.

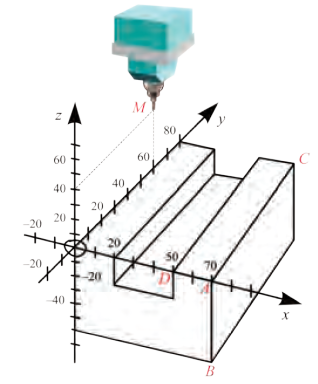
a) Tìm toạ độ các điểm A, B, C, D.

b) Viết phương trình mặt phẳng \((ABC)\) và mặt phẳng \((ACD)\).

c) Viết phương trình tham số của đường thẳng AC.

d) Cho biết đầu mũi tiện đang đặt tại điểm \(M(0;60;40)\). Tính khoảng cách từ \(M\) đến mặt phẳng \((ABC)\).

Tại một thời điểm có bão, khi đặt hệ trục toạ độ Oxyz (đơn vị trên mỗi trục là kilômét) ở một vị trí phù hợp thì tâm bão có tọ̣a độ \((300;200;1)\).

a) Lập phương trình mặt cầu để mô tả ranh giới bên ngoài vùng ảnh hưởng của bão ở cấp độ: bán kính gió mạnh từ cấp 10 , giật từ cấp 12 trở lên khoảng 100 km tính từ tâm bão.

b) Tại một vị trí có tọa độ \((350;245;1)\) thì có bị ảnh hưởng bởi cơn bão được mô tả ở câu a) không?

Hệ thống định vị toàn cầu (tên tiếng Anh là: Global Positioning System, viết tắt là GPS) là một hệ thống cho phép xác định chính xác vị trí của một vật thể trong không gian (Hinh 5).

Ta có thể mô phỏng cơ chế hoạt động của hệ thống GPS trong không gian như sau: Trong cùng một thời điểm, toạ độ của một điểm \(M\) trong không gian sẽ được xác định bởi bốn vệ tinh cho trước, trên mỗi vệ tinh có một máy thu tín hiệu. Bằng cách so sánh sự sai lệch về thời gian từ lúc tín hiệu được phát đi với thời gian nhận phản hồi tín hiệu đó, mỗi máy thu tín hiệu xác định được khoảng cách từ vệ tỉh đến vị trí \(M\) cần tìm toạ độ. Như vậy, điểm \(M\) là giao điểm của bốn mặt cầu với tâm lần lượt là bốn vệ tinh đã cho.

Giả sử trong không gian với hệ tọa độ Oxyz, cho bốn vệ tinh \(A(3; - 1;6)\), \(B(1;4;8),C(7;9;6),D(7; - 15;18)\). Tìm toạ độ của điểm \(M\) trong không gian, biết khoảng cách từ các vệ tinh đến điểm \(M\) lần lượt là \(MA = 6,MB = 7,MC = 12\), \(MD = 24\).

Một nguồn âm phát ra sóng âm là sóng cầu (mặt đầu sóng là mặt cầu). Khi gắn trên hệ trục toạ độ Oxyz với đơn vị trên mỗi trục là mét, vị trí nguồn âm có tọa độ \((2;3;1)\), cường độ âm chuẩn phát ra có bán kính 10 m .

a) Lập phương trình mặt cầu mô tả ranh giới nhận được cường độ âm chuẩn.

b) Tại một vị trí có tọa độ \((5;0;2)\) có nhận được cường độ âm chuẩn từ nguồn âm trên hay không?

Trong không gian với hệ toạ độ Oxyz (đơn vị trên mỗi trục là kilômét), một trạm thu phát sóng điện thoại di động (Hình vẽ ) được đặt ở vị trí \(I( - 3;2;7)\).

a) Sử dụng phương trình mặt cẩu để mô tả ranh giới bên ngoài của vùng phủ sóng trong không gian, biết rằng trạm thu phát sóng đó được thiết kế với bán kính phủ sóng là 3 km .

b) Điểm \(A( - 2;1;8)\) nằm trong hay nằm ngoài mặt cầu đó? Nếu người dùng điện thoại ở điểm \(A( - 2;1;8)\) thì có thể sử dụng dịch vụ của trạm này hay không?

c) Điểm \(B(2;3;4)\) nằm trong hay nằm ngoài mặt cầu đó? Nếu người dùng điện thoạiở điểm \(B(2;3;4)\) thì có thể sử dụng dịch vụ của trạm này hay không?

Trong không gian vối hệ toạ độ Oxyz (đơn vị trên mỗi trục là mét), một ngọn hải đăng (Hình vẽ) được đặt ở vị trí \(I(21;35;50)\).

a) Sử dụng phương trình mặt cầu để mô tả ranh giởi của vùng phủ sáng trên biển của hải đăng, biết rằng ngọn hải đăng đó được thiết kế vởi bán kính phủ sáng là 4 km .

b) Nếu người đi biển ở vị trí \(C(42;37;0)\) thì có thể nhìn thấy được ánh sáng từ ngọn hải đăng

c) Nếu người đi biển ở vị trí \(D(5121;658;0)\) thì có thể nhìn thấy được ánh sáng từ ngọn hải đăng hay không?

d) Giả sử người đi biển di chuyển theo đường thẳng từ vị trí \(I(21;35;50)\) đến vị trí \(D(5121;658;0)\). Tìm vị trí cuối cùng trên đoạn thẳng ID sao cho người đi biển còn có thể nhìn thấy được ánh sáng từ ngọn hải đăng.

Hệ thống định vị toàn cầu (tên tiếng Anh là: Global Positioning System, viết tắt là GPS) là một hệ thống cho phép xác định chính xác vị trí của một vật thể trong không gian (Hình 42).

Ta có thể mô phỏng cơ chế hoạt động của hệ thống GPS trong không gian như sau: Trong cùng một thời điểm, toạ độ của một điểm \(M\) trong không gian sẽ được xác định bởi bốn vệ tinh cho trước, trên mỗi vệ tinh có một máy thu tín hiệu. Bằng cách so sánh sự sai lệch về thời gian từ lúc tín hiệu được phát đi vối thời gian nhận phản hồi tín hiệu đó, mỗi máy thu tín hiệu xác định được khoảng cách từ vệ tinh đến vị trí \(M\) cần tìm toạ độ. Như vậy, điểm \(M\) là giao điểm của bốn mặt cầu vối tâm lần lượt là bốn vệ tinh đã cho.

Ta xét một ví dụ cụ thể như sau:

Trong không gian với hệ tọa độ Oxyz, cho bốn vệ tinh \(A(3; - 1;6),B(1;4;8)\), \(C(7;9;6),D(7; - 15;18)\). Tìm toạ độ của điểm \(M\) trong không gian biết khoảng cách từ các vệ tinh đến điểm \(M\) lần lượt là \(MA = 6,MB = 7,MC = 12,MD = 24\).

Hình vẽ minh hoạ đường bay của một chiếc trực thăng \(H\) cất cánh từ một sân bay. Xét hệ trục tọa độ Oxyz có gốc tọa độ \(O\) là chân tháp điều khiển của sân bay; trục Ox là hưởng đông, trục Oy là hướng bắc và trục Oz là trục thẳng đứng, đơn vị trên mỗi trục là kilômét.

Trực thăng cất cánh từ điểm \(G\). Vectơ \(\vec r\) chỉ vị trí của trực thăng tại thời điểm \(t\) phút sau khi cất cánh \((t \ge 0)\) có toạ độ là: \(\vec r = (1 + t;0,5 + 2t;2t)\).

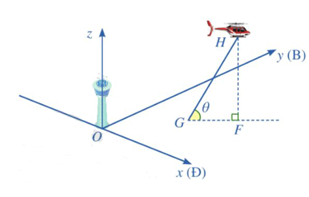
a) Tìm góc \(\theta \) mà đường bay tạo với phương ngang.

b) Lập phương trình đường thẳng GF, trong đó \(F\) là hình chiếu của điểm \(H\) lên mặt phẳng \((Oxy)\).

c) Trực thăng bay vào mây ở độ cao 2 km . Tìm tọ̣ độ điểm mà máy bay trực thăng bắt đầu đi vào đám mây.

d) Giả sử một đỉnh núi nằm ở điểm \(M(5;4,5;3)\). Tìm giá trị của \(t\) khi HM vuông góc với đường bay GH. Tìm khoảng cách từ máy bay trực thăng đến đỉnh núi tại thời điểm đó.

Trong không gian với hệ toạ độ Oxyz, đài kiểm soát không lưu sân bay có toạ độ \(O(0;0;0)\), mỗi đơn vị trên trục ứng với 1 km . Máy bay bay trong phạm vi cách đài kiểm soát 417 km sẽ hiển thị trên màn hình ra đa. Một máy bay đang ở vị trí \(A( - 688; - 185;8)\), chuyển động theo đường thẳng \(d\) có vectơ chỉ phương là \(\vec u = (91;75;0)\) và hướng về đài kiểm soát không lưu (Hình vẽ).

a) Xác định tọa độ của vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa.

b) Xác định tọa độ của vị trí mà máy bay bay gần đài kiểm soát không lưu nhất. Tính khoảng cách giữa máy bay và đài kiểm soát không lưu lúc đó.

c) Xác định toạ độ của vị trí mà máy bay ra khỏi màn hình ra đa.