(Trả lời ngắn) 16 bài tập Khảo sát và vẽ đồ thị một số hàm số cơ bản (có lời giải)

Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ.

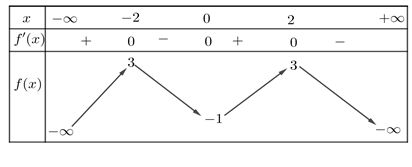
Số nghiệm của phương trình \(2f\left( x \right) + 5 = 0\) là

Đồ thị hàm số \[y = (x - 1)({x^2} - 4x + 4)\] có bao nhiêu điểm chung với trục \[Ox\]?

Cho hàm số \(y = \frac{{{x^3}}}{3} + {x^2} - 2x + 1\) có đồ thị. Phương trình tiếp tuyến của tại điểm \(M\left( {1;\frac{1}{3}} \right)\) là

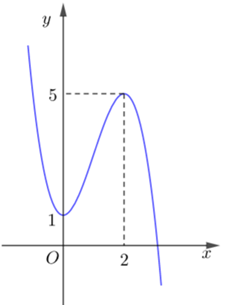
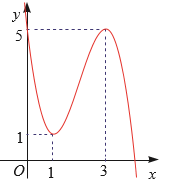
Cho hàm bậc ba \(y = f\left( x \right)\) có đồ thị trong hình bên. Số nghiệm của phương trình \(f\left( x \right) = 2\) là

Tiếp tuyến của đồ thị hàm số \(y = {x^3} - 2{x^2} + 3x - 1\) tại điểm có hoành độ \(x =  - 1\) có hệ số góc \(k\) bằng

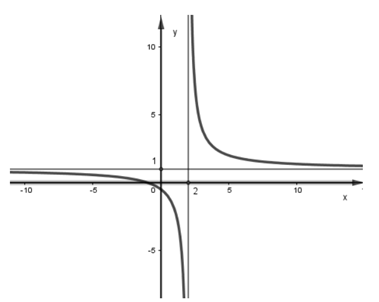
Cho hàm số \(y = \frac{{ax + 1}}{{bx - 2}}\) có đồ thị như hình vẽ. Tính \(T = a + b\).

Trong 20 phút theo dôi, lưu lượng nước của một con sông được tính theo công thức \({\rm{Q}}\left( {\rm{t}} \right) =  - \frac{1}{5}{t^3} + 5{t^2} + 100\), trong đó Q được tính theo \({{\rm{m}}^3}/\) phút, \({\rm{t}}\) tính theo phút, \(0 \le {\rm{t}} \le 20\) (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016). Khi lưu lượng nước của con sông lên đến \(550{\rm{\;}}{{\rm{m}}^3}/\) phút thì cảnh báo lũ được đưa ra.

Trong thời gian theo dōi, lưu lượng nước của con sông lớn nhất là bao nhiêu? Cảnh báo lũ được đưa ra vào thời điếm nào?

Khi một vật lạ mắc kẹt trong khí quản khiến ta phải ho, cơ hoành đẩy lên trên gây ra tăng áp lực trong phổi, theo đó cuống họng co thắt làm hẹp khí quản khiến không khí đi qua mạnh hơn. Đối với một lượng không khí bị đẩy ra trong một khoảng thời gian cố định, khí quản càng nhỏ thì luồng không khí càng đẩy ra nhanh hơn. Vận tốc luồng khí thoát ra càng cao, lực tác động lên vật lạ càng lớn. Qua nghiên cứu một số trường hợp, người ta nhận thấy vận tốc \(v\) của luồng khí liên hệ với bán kính \(x\) của khí quản theo công thức: \(v(x) = k({x_0} - x){x^2}\) với \(\frac{1}{2}{x_0} \le x \le {x_0}\). Trong đó \(k\) là hằng số \((k > 0)\) và \({x_0}\) là bán kính khí quản ở trạng thái bình thường. Tìm \(x\) theo \({x_0}\) để vận tốc của luồng khí một cơn ho trong trường hợp này là lớn nhất.

Anh Nam có một mảnh đất rộng và muốn dành ra một khu đất hình chữ nhật có diện tích \(200{\rm{\;}}{{\rm{m}}^2}\) để trồng vài loại cây mới. Anh dự kiến rào quanh ba cạnh của khu đất hình chữ nhật này bằng lưới thép, cạnh còn lại (chiều dài) sẽ tận dụng bức tường có sẵn (Hình 1.36). Do điều kiện địa lí, chiều rộng khu đất không vượt quá \(15{\rm{\;m}}\), hỏi chiều rộng của khu đất này bằng bao nhiêu để tổng chiều dài lưới thép cần dùng là ngắn nhất (nghĩa là chi phí rào lưới thép thấp nhất)?

Giả sử số lượng của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hoá bằng hàm số \(P\left( t \right) = \frac{a}{{b + {e^{ - 0,75t}}}}\), trong đó thời gian \(t\) được tính bằng giờ. Tại thời điểm ban đầu \(t = 0\), quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ. Tìm các giá trị của \(a\) và \(b\). Theo mô hình này, điều gì xảy ra với quần thể nấm men về lâu dài?

Một nhà sản xuất cần làm những hộp đựng hình trụ có thể tích 1 lít. Tìm các kích thước của hộp đựng để chi phí vật liệu dùng để sản xuất là nhỏ nhất (kết quả được tính theo centimét và làm tròn đến chữ số thập phân thứ hai).

Cho hàm số y = x³ − 3x² + 2. Tìm tọa độ điểm I  là trung điểm của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số.

Cho hàm số bậc ba y = f (x) có đồ thị như Hình vẽ. Tìm công thức của hàm số.

Khi bỏ qua sức cản của không khí, độ cao (mét) của một vật được phóng thẳng đứng lên trên từ điểm cách mặt đất 2 m với vận tốc ban đầu 24,5 m/s là h(t) = 2+24,5t – 4,9t² (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016).

a) Tìm vận tốc của vật sau 2 giây.

b) Khi nào vật đạt độ cao lớn nhất và độ cao lớn nhất đó là bao nhiêu?

c) Khi nào thì vật chạm đất và vận tốc của vật lúc chạm đất là bao nhiêu?

Một phần đường ray tàu lượn siêu tốc có dạng đồ thị hàm số bậc ba: y = f(x) = ax3 + bx2 + cx + d, (\[a \ne 0\]). Trục Ox mô tả quãng đường tàu di chuyển theo chiều ngang (tính bằng centimét), trục Oy mô tả chiều cao của đường ray (tính bằng centimét) tại mỗi vị trí x. Chiều cao xuất phát là 50 cm. Tàu xuống dưới mặt đất lần thứ nhất từ vị trí x = 20 cm, tàu lên khỏi mặt đất ở vị trí x = 50 cm và sau đó xuống dưới mặt đất lần thứ hai ở vị trí x = 100 cm.

Xét đồ thị của hàm số đã cho khi x \[ \in \] [0; 100] như hình vẽ:

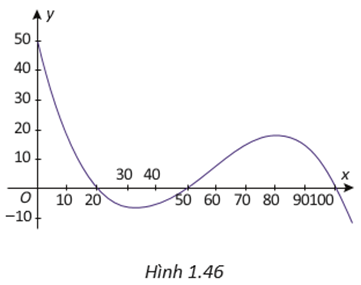
a) Tìm công thức hàm số f(x).

b) Tìm điểm cao nhất của đường ray khi tàu lên khỏi mặt đất và toạ độ điểm thấp nhất của đường ray khi tàu xuống dưới mặt đất.