(Đúng sai) 18 bài tập Khảo sát và vẽ đồ thị một số hàm số cơ bản (có lời giải)
72 câu hỏi
a) \(f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty \,;\,1} \right)\).
b) \(f\left( x \right)\) đạt cực đại tại \(x = 1\).
c) \(f\left( x \right)\) đồng biến trên khoảng \(\left( { - 1\,;\,1} \right)\).
d) \(f\left( x \right)\) có cực đại bằng \(0\).
a) Hàm số \(y = f\left( x \right)\) có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1.
b) Hàm số \(y = f\left( x \right)\) có đúng một cực trị.
c) Hàm số \(y = f\left( x \right)\) đạt cực đại tại \(x = 0\) và đạt cực tiểu tại \(x = 1\).
d) Hàm số \(y = f\left( x \right)\) có giá trị cực tiểu bằng 1.
a) Hàm số \[y = f\left( x \right)\] chỉ có một cực trị.
b) Hàm số \[y = f\left( x \right)\] nghịch biến trên khoảng \[\left( {0;1} \right)\].
c) Giá trị nhỏ nhất của hàm số \[y = f\left( x \right)\] trên \[\mathbb{R}\] bằng \[ - 1\].
d) Giá trị lớn nhất của hàm số \[y = f\left( x \right)\] trên \[\mathbb{R}\] bằng \[0\].
Cho hàm số \(f\left( x \right) = {x^3} - 3x + 1\). Các mệnh đề sau đúng hay sai?
a) Đồ thị hàm số có đường tiệm cận ngang.
Cho hàm số \(f\left( x \right) = {x^3} - 3x + 1\). Các mệnh đề sau đúng hay sai?
b) Điểm cực đại của đồ thị hàm số là \[M\left( {1\,; - 1} \right)\].
Cho hàm số \(f\left( x \right) = {x^3} - 3x + 1\). Các mệnh đề sau đúng hay sai?
c) Hàm số đồng biến trên các khoảng \(\left( { - \infty \,; - 1} \right)\) và \(\left( {1\,; + \infty } \right)\).
Cho hàm số \(f\left( x \right) = {x^3} - 3x + 1\). Các mệnh đề sau đúng hay sai?
d) Hàm số không có cực trị.
a) Hàm số có giá trị nhỏ nhất bằng \[ - 1\].
b) Đồ thị hàm số có đúng hai đường tiệm cận đứng.
c) Đồ thị hàm số và trục hoành có hai điểm chung.
d) Hàm số đồng biến trên khoảng \[\left( { - 1; + \infty } \right)\].
Các mệnh đề sau đúng hay sai?
a) Cho hàm số \(y = f\left( x \right)\) có đồ thị như đường cong hình dưới. Phương trình \(f\left( x \right) = 1\)có 2 nghiệm
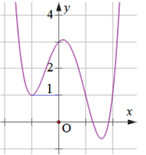
Các mệnh đề sau đúng hay sai?
b) Số giao điểm của đồ thị hàm số \(y = {x^4} - 3{x^2} - 4\) và trục hoành là 3
Các mệnh đề sau đúng hay sai?
c) Số giao điểm của đường cong \[y = {x^3} - 2{x^2} + x - 1\] và đường thẳng \[y = 1 - 2x\] là 0
Các mệnh đề sau đúng hay sai?
d) Cho hàm số \[y = {x^3} + x + 2\] có đồ thị \[\left( C \right)\]. Số giao điểm của \[\left( C \right)\] và đường thẳng \[y = 2\] là 2
a) Hàm số \(f\left( x \right)\) đạt cực đại tại \(x = 3\).
b) Hàm số \(f\left( x \right)\)nghịch biến trên \(\left( { - \infty - 3} \right)\).
c) Hàm số \(f\left( x \right)\)đồng biến trên \(\left( {3; + \infty } \right)\).
d) \(f\left( x \right) \ge 0\), \(\forall x \in \mathbb{R}\).
a) Hàm số có giá trị nhỏ nhất là \( - 4\).
b) Giá trị cực đại của hàm số là 5 .
c) Hàm số có một điểm cực đại và hai điểm cực tiểu.
d) Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 3} \right)\) và \(\left( {1;2} \right)\).
a) Hàm số đạt cực tiểu tại \(x = - 2\).
b) \(\mathop {Min}\limits_{\left( {0;3} \right)} y = - 2\).
c) Đồ thị hàm số có một đường tiệm cận ngang.
d) Hàm số nghịch biến trên khoảng \(\left( { - \infty ; + \infty } \right)\).
a) Hàm số đạt cực đại tại điểm \(x = - 3\) và đạt cực tiểu tại \(x = - 1\).
b) Đồ thị hàm số nhận đường thẳng \(x = - 2\) làm tiệm cận đứng.
c) Hàm số nghịch biến trên khoảng \(\left( { - 3; - 1} \right)\).
d) Đồ thị hàm số không có điểm chung với trục hoành.
a) Hàm số có đúng một cực trị.
b) Hàm số có giá trị cực tiểu bằng \[1\].
c) Hàm số có giá trị lớn nhất bằng \[0\]và giá trị nhỏ nhất bằng \[1\].
d) Hàm số đạt cực đại tại \(x = 0\)và đạt cực tiểu tại \(x = 1\).
a) Đồ thị hàm số có đường tiệm cận đứng\[x = 2\].
b) Hàm số có đúng \[1\] điểm cực trị.
c) Hàm số đạt giá trị lớn nhất bằng \(2\) tại \(x\) bằng \(4\).
d) Hàm số đồng biến trên khoảng \(\left( {2;3} \right)\).
a) Hàm số \(y = f\left( x \right)\) có điểm cực tiểu \(x = 1\).
b) Hàm số \(y = f\left( x \right)\) không có cực trị.
c) Phương trình \(f\left( x \right) = 0\) vô nghiệm.
d) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty \,;\,0} \right)\).
Các mệnh đề sau đúng hay sai?
a) Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\)có đồ thị trong hình bên.phương trình \(a{x^3} + b{x^2} + cx + d = 0\) có ba nghiệm
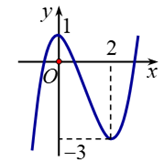
Các mệnh đề sau đúng hay sai?
b) Đồ thị hàm số \(y = {x^3} - 2x + 4\)và đường thẳng \(y = x + 2\)có 3 điểm chung
Các mệnh đề sau đúng hay sai?
c) Tâm đối xứng của đồ thị hàm số \(y = \frac{{x - 1}}{{x + 1}}\) có tọa độ là\(\left( { - \,1\,;\,0} \right)\)
Các mệnh đề sau đúng hay sai?
d) Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\)và có bảng biến thiên như sau:
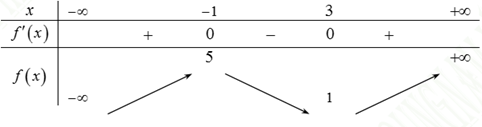Phương trình \(f\left( x \right) - 2 = 0\) có tất cả bao nhiêu nghiệm 3
a) Hàm số đạt cực đại tại \(x = 0\) và đạt cực tiểu tại \(x = 1\).
b) Hàm số có giá trị cực tiểu bằng \(1\).
c) Hàm số có giá trị lớn nhất bằng \(2\) và giá trị nhỏ nhất bằng \( - 3\).
d) Hàm số có đúng một cực tiểu và không có cực đại.
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {x^2}\left( {x + 1} \right)\left( {{x^2} - 1} \right)\), với \(\forall x \in \mathbb{R}\). Các mệnh đề sau đúng hay sai?
a) Hàm số đã cho nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\).
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {x^2}\left( {x + 1} \right)\left( {{x^2} - 1} \right)\), với \(\forall x \in \mathbb{R}\). Các mệnh đề sau đúng hay sai?
b) Hàm số đã cho có \(3\) cực trị.
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {x^2}\left( {x + 1} \right)\left( {{x^2} - 1} \right)\), với \(\forall x \in \mathbb{R}\). Các mệnh đề sau đúng hay sai?
c) Hàm số đã cho đồng biến trên \(\mathbb{R}\).
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {x^2}\left( {x + 1} \right)\left( {{x^2} - 1} \right)\), với \(\forall x \in \mathbb{R}\). Các mệnh đề sau đúng hay sai?
d) Hàm số đã cho nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).
a) Hàm số \(y = f\left( x \right)\) có hai điểm cực trị.
b) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
c)\(f\left( 1 \right) > f\left( 2 \right) > f\left( 4 \right)\).
d) Trên đoạn \(\left[ { - 1;4} \right]\), giá trị lớn nhất của hàm số \(y = f\left( x \right)\) là \(f\left( 1 \right)\).
a) \[f\left( { - 3} \right) < f\left( { - 2} \right)\]
b) Hàm số \[f\left( x \right)\]đồng biến trên khoảng \[\left( { - \infty \,;\, - 1} \right)\].
c) \[f\left( 0 \right) < f\left( 1 \right)\].
d) Hàm số \[f\left( x \right)\]đạt cực đại tại \[x = 0\].
